Эквивалентность функциональных зависимостей

Для понимания эквивалентности наборов функциональных зависимостей (наборов FD) в этой статье дано основное представление о замыкании атрибутов.

Учитывая Отношение с разными наборами FD для этого отношения, мы должны выяснить, является ли один набор FD подмножеством другого или оба равны.

Как найти взаимосвязь между двумя наборами FD?

Пусть FD1 и FD2 - два множества FD для отношения R.

1. Если все FD в FD1 могут быть получены из FD, присутствующих в FD2, мы можем сказать, что FD2 ⊃ FD1.
2. Если все FD в FD2 могут быть получены из FD, присутствующих в FD1, мы можем сказать, что FD1 ⊃ FD2.
3. Если 1 и 2 истинны, FD1 = FD2.

Все эти три случая можно показать с помощью диаграммы Венна как: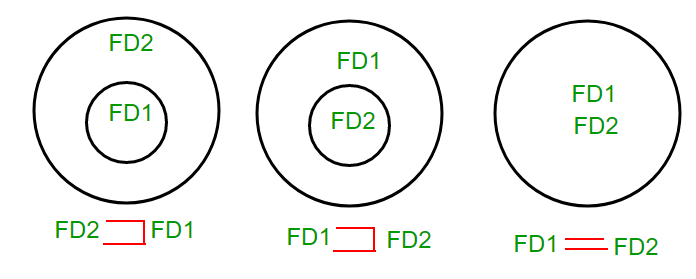

В. Давайте возьмем пример, чтобы показать взаимосвязь между двумя наборами FD. Отношение R (A, B, C, D), имеющее два набора FD, FD1 = {A-> B, B-> C, AB-> D} и FD2 = {A-> B, B-> C, A- > C, A-> D}

Шаг 1. Проверка, все ли FD FD1 присутствуют в FD2.

• A-> B в наборе FD1 присутствует в наборе FD2.
• B-> C в наборе FD1 также присутствует в наборе FD2.
• AB-> D присутствует в наборе FD1, но не непосредственно в FD2, но мы проверим, можем ли мы его получить или нет. Для множества FD2 (AB) ⁺ = {A, B, C, D}. Это означает, что AB может функционально определять A, B, C и D. Таким образом, AB-> D также будет сохраняться в множестве FD2.

Поскольку все FD в наборе FD1 также сохраняются в наборе FD2, FD2 ⊃ FD1 истинно.

Шаг 2. Проверка, все ли FD из FD2 присутствуют в FD1.

• A-> B в наборе FD2 присутствует в наборе FD1.
• B-> C в наборе FD2 также присутствует в наборе FD1.
• A-> C присутствует в FD2, но не непосредственно в FD1, но мы проверим, можем ли мы его получить или нет. Для набора FD1 (A) ⁺ = {A, B, C, D}. Это означает, что A может функционально определять A, B, C и D. SO A-> C также будет сохраняться в наборе FD1.
• A-> D присутствует в FD2, но не непосредственно в FD1, но мы проверим, можем ли мы его получить или нет. Для набора FD1 (A) ⁺ = {A, B, C, D}. Это означает, что A может функционально определять A, B, C и D. SO A-> D также будет сохраняться в наборе FD1.

Поскольку все FD в наборе FD2 также сохраняются в наборе FD1, FD1 ⊃ FD2 истинно.

Шаг 3. Поскольку FD2 ⊃ FD1 и FD1 ⊃ FD2 истинны, FD2 = FD1 истинно. Эти два набора FD семантически эквивалентны.

В. Давайте возьмем другой пример, чтобы показать взаимосвязь между двумя наборами FD. Отношение R2 (A, B, C, D), имеющее два набора FD, FD1 = {A-> B, B-> C, A-> C} и FD2 = {A-> B, B-> C, A- > D}

Шаг 1. Проверка, все ли FD FD1 присутствуют в FD2.

• A-> B в наборе FD1 присутствует в наборе FD2.
• B-> C в наборе FD1 также присутствует в наборе FD2.
• A-> C присутствует в FD1, но не непосредственно в FD2, но мы проверим, можем ли мы его получить или нет. Для набора FD2 (A) ⁺ = {A, B, C, D}. Это означает, что A может функционально определять A, B, C и D. SO A-> C также будет сохраняться в наборе FD2.

Поскольку все FD в наборе FD1 также сохраняются в наборе FD2, FD2 ⊃ FD1 истинно.

Шаг 2. Проверка, все ли FD из FD2 присутствуют в FD1.

• A-> B в наборе FD2 присутствует в наборе FD1.
• B-> C в наборе FD2 также присутствует в наборе FD1.
• A-> D присутствует в FD2, но не непосредственно в FD1, но мы проверим, можем ли мы его получить или нет. Для набора FD1 (A) ⁺ = {A, B, C}. Это означает, что A не может функционально определить D. SO A-> D не будет удерживаться в FD1.

Поскольку все FD в наборе FD2 не сохраняются в наборе FD1, FD2 ⊄ FD1.

Шаг 3. В этом случае FD2 ⊃ FD1 и FD2 ⊄ FD1, эти два набора FD не являются семантически эквивалентными.

Эта статья предоставлена Sonal Tuteja. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное или хотите поделиться дополнительной информацией по теме, обсужденной выше.