Доверительный интервал

Предпосылки: t-тест, z-тест

Проще говоря, доверительный интервал - это диапазон, в котором мы уверены, что существует истинное значение. Выбор уровня достоверности для интервала определяет вероятность того, что доверительный интервал будет содержать истинное значение параметра. Этот диапазон значений обычно используется для работы с популяционными данными, для извлечения конкретной ценной информации с определенной степенью уверенности, отсюда и термин «доверительный интервал».

Рис. 1. Показывает, как в целом выглядит доверительный интервал.

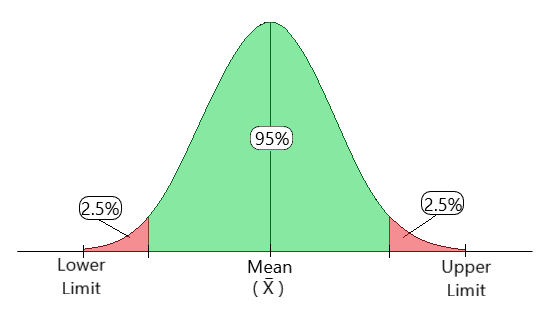
Рис.1: Иллюстрация доверительного интервала

Уровень уверенности:

Уровень достоверности описывает неопределенность, связанную с методом отбора проб.

Предположим, мы использовали один и тот же метод выборки (скажем, выборочное среднее), чтобы вычислить разные интервальные оценки для каждой выборки. Некоторые интервальные оценки будут включать истинный параметр численности, а некоторые нет.

Уровень достоверности 90% означает, что мы ожидаем, что 90% интервальных оценок будут включать параметр генеральной совокупности. Уровень достоверности 95% означает, что 95% интервалов будут включать параметр совокупности.

Например, предположим, что вы изучаете средний рост мужчин в определенном городе. Чтобы найти это, вы устанавливаете уровень достоверности 95% и обнаруживаете, что доверительный интервал 95% равен (168 182). Это означает, что если вы будете повторять это снова и снова, в 95% случаев рост мужчины упадет где-то между 168 и 182 см.

Построение доверительного интервала:

Построение доверительного интервала включает 4 шага.

 Шаг 1. Определите проблему с образцом. Выберите статистику (например, выборочное среднее и т. Д.), Которая 
    вы будете использовать для оценки параметра численности.

Шаг 2: Выберите уровень достоверности. (Обычно это 90%, 95% или 99%)

Шаг 3: Найдите погрешность. (Обычно приводится) Если не указано, используйте следующую формулу: -
    Погрешность = Критическое значение * Стандартное отклонение

Шаг 4: Укажите доверительный интервал. Неопределенность обозначается уровнем достоверности. 
    А диапазон доверительного интервала определяется уравнением-1 .

Уравнение-1

 где, 
Sample_Statistic -> Может быть любой статистикой. (например, выборочное среднее)
Margin_of_Error -> обычно это (± 2.5)

Расчет доверительного интервала

Для расчета CI требуются два статистических параметра.

• Среднее (μ) - Среднее арифметическое - это среднее значение чисел. Он определяется как сумма n чисел, деленная на количество чисел до n. (Уравнение-2)

• Стандартное отклонение (σ) - Это мера того, насколько разбросаны числа. Он определяется как сумма квадратов разницы между каждым числом и средним значением. (Уравнение-3)

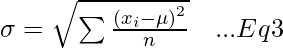
а) Использование t-распределения

Мы используем t-распределение, когда размер выборки n <30 .

Рассмотрим следующий пример. Была взята случайная выборка из 10 бойцов UFC и измерен их вес. Средний вес составил 240 кг. Постройте оценку 95% доверительного интервала для среднего веса. Стандартное отклонение выборки составило 25 кг. Найдите доверительный интервал для выборки истинного среднего веса всех бойцов UFC.

 Шаг 1. Вычтите 1 из размера выборки. [Уравнение-4] 
     Это дает степени свободы (df) , требуемые на шаге 3.  

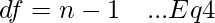
 где, 
df = степень свободы
n = размер выборки 

Используя уравнение-4, мы получаем df = 10 - 1 = 9.

 Шаг 2 - Вычтите доверительный интервал из 1, затем разделите на два.
 [Уравнение-5]
     Это дает уровень значимости (α) , необходимый для шага 3.

 α = уровень значимости
CL = уровень уверенности

Используя уравнение-5, получаем α = (1 - 0,95) / 2 = 0,025

 Шаг 3 - Используйте значения α и df в таблице t-распределения и найдите значение t .  

Используя значения df и α в таблице t-распределения, получаем t = 2,262.

 Шаг 4 - Используйте значение t, полученное на шаге 3, в формуле для доверительного интервала. 
      с t-распределением. [Уравнение-6]

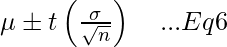
 где,
μ = среднее
t = выбранное значение t из таблицы выше
σ = стандартное отклонение
n = количество наблюдений

Итак, подставляя значения в уравнение 6, мы получаем

 где,
Нижний предел = 222,117
Верхний предел = 257,883

Таким образом, мы на 95% уверены, что истинный средний вес бойцов UFC составляет от 222,117 до 257,883.

б) Использование z-распределения

Мы используем z-распределение, когда размер выборки n> 30. Z-тест более полезен, когда известно стандартное отклонение.

Рассмотрим следующий пример. Была взята случайная выборка из 50 взрослых самок и измерено количество их эритроцитов. Среднее значение выборки составляет 4,63, а стандартное отклонение количества эритроцитов - 0,54. Постройте 95% -ный доверительный интервал для истинного среднего количества эритроцитов у взрослых женщин.

 Шаг 1 - Найдите среднее значение. [Уравнение-2] (если еще не указано)
Шаг 2 - Найдите стандартное отклонение. [Уравнение-3] (если еще не дано)
Шаг 3 - Определите z-значение для указанного доверительного интервала. 
     (некоторые общие значения в таблице ниже)

 Шаг 4 - Используйте значение z, полученное на шаге 3, в формуле для доверительного интервала. 
      с z-распределением. [Уравнение-7]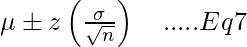

 где,
μ = среднее
z = выбранное значение z из таблицы выше
σ = стандартное отклонение
n = количество наблюдений

Подставляя значения в уравнение-7, мы получаем

 где,
Нижний предел = 4,480
Верхний предел = 4,780

Таким образом, мы на 95% уверены, что истинное среднее количество эритроцитов у взрослых женщин составляет от 4,480 до 4,780.

Доверительный интервал - одна из основополагающих концепций статистики. Он сообщает заявление о данных. На основе имеющихся данных могут использоваться различные методы выборки, такие как среднее значение, медиана и т. Д. Также можно определить, какое распределение использовать и когда для получения наилучших результатов. Если возникнут сомнения / вопросы, оставьте комментарий ниже.