Дерево Прото Ван Эмде Боас | Набор 6 | Запрос: преемник и предшественник

Опубликовано: 13 Января, 2022

Пожалуйста, сначала ознакомьтесь со всеми предыдущими статьями о Древе Прото Ван Эмде Боаса.

Процедура запроса преемника:

Базовый случай: для Proto-VEB размера 2 единственная возможность состоит в том, что ключ равен 0, и если следующий ключ присутствует, то он является его преемником или нет преемника. Таким образом, применяется та же процедура.
Рекурсия:
- Во-первых, мы посмотрим в текущем кластере (означает кластер, в котором присутствует ключ запроса), если есть какой-либо ключ, больший, чем присутствует ключ запроса, тогда мы будем преемником, поэтому мы его возвращаем.
- Если это не так, то мы рекурсивно вызовем процедуру-преемник поверх сводки, чтобы найти следующее истинное значение в сумме. Если в сводке нет следующего истинного значения, мы вернем -1 как знак того, что нет большего ключа.
- В вышеупомянутой операции, если мы найдем любое следующее истинное значение, мы найдем минимальный ключ, присутствующий в этом кластере, который будет преемником ключа запроса.

См. Изображение ниже для базового понимания работы запроса преемника: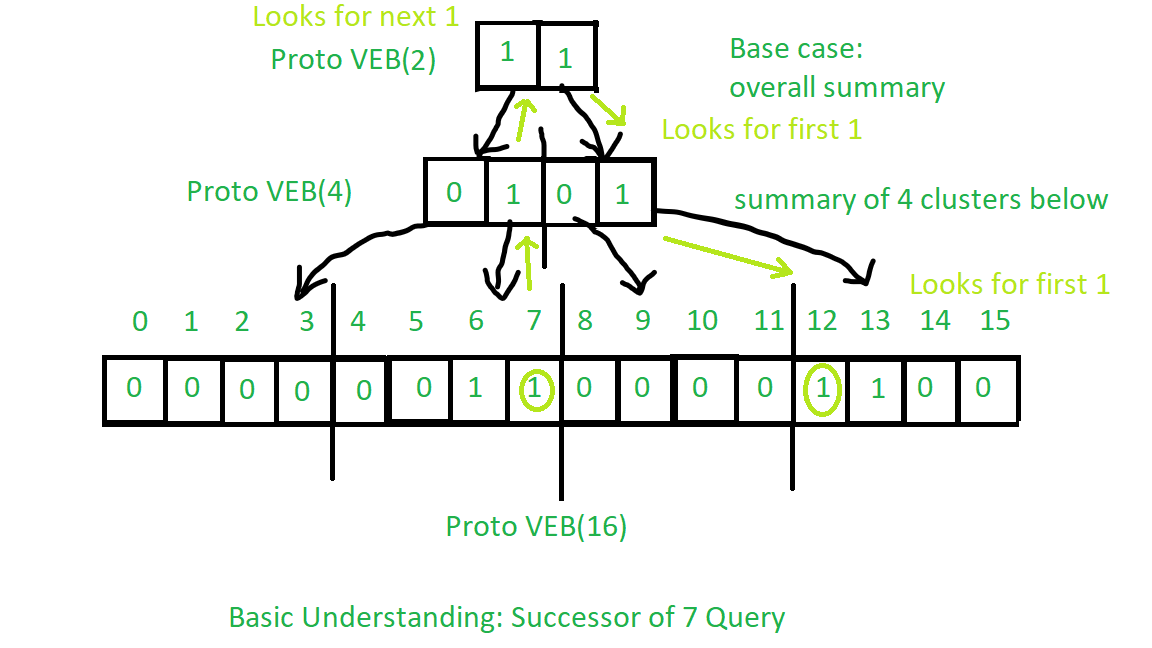

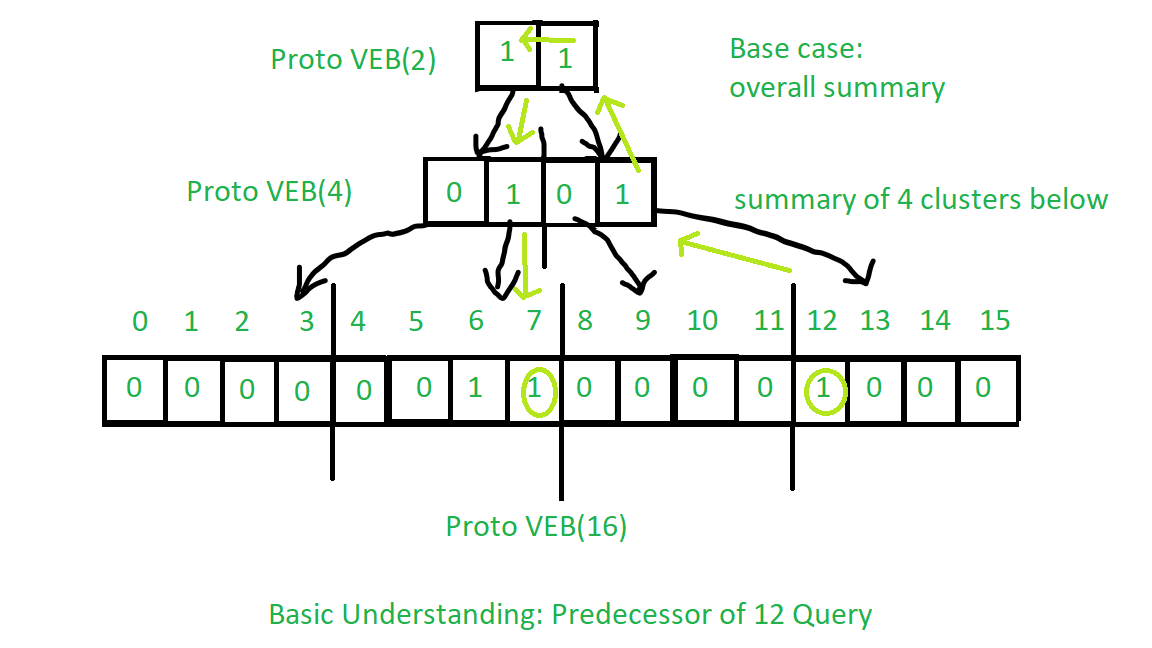
Процедура для предшественника такая же, как для преемника с некоторыми незначительными изменениями, вы должны попытаться понять это из приведенного выше описания для запроса преемника. См. Изображение ниже для базового понимания:

Below is the implementation:

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
  
class Proto_Van_Emde_Boas {
public:
    // Total number of keys
    int universe_size;
  
    // Summary
    Proto_Van_Emde_Boas* summary;
  
    // Clusters array of Proto-VEB pointers
    vector<Proto_Van_Emde_Boas*> clusters;
  
    int root(int u)
    {
        return int(sqrt(u));
    }
  
    // Function to return cluster numbers
    // in which key is present
    int high(int x)
    {
        return x / root(universe_size);
    }
  
    // Function to return position of x in cluster
    int low(int x)
    {
        return x % root(universe_size);
    }
  
    // Function to return the index from
    // cluster number and position
    int generate_index(int cluster, int position)
    {
        return cluster * root(universe_size) + position;
    }
  
    // Constructor
    Proto_Van_Emde_Boas(int size)
    {
        universe_size = size;
  
        // Base case
        if (size <= 2) {
  
            // Set summary to nullptr as there is no
            // more summary for size 2
            summary = nullptr;
  
            // Vector of two pointers
            // nullptr in starting
            clusters = vector<Proto_Van_Emde_Boas*>(size, nullptr);
        }
        else {
  
            // Assiging Proto-VEB(sqrt(u)) to summary
            summary = new Proto_Van_Emde_Boas(root(size));
  
            // Creating array of Proto-VEB Tree pointers of size sqrt(u)
            // first all nullptrs are going to assign
            clusters = vector<Proto_Van_Emde_Boas*>(root(size), nullptr);
  
            // Assigning Proto-VEB(sqrt(u)) to all its clusters
            for (int i = 0; i < root(size); i++) {
                clusters[i] = new Proto_Van_Emde_Boas(root(size));
            }
        }
    }
};
  
// Function that returns true if the
// key is present in the tree
bool isMember(Proto_Van_Emde_Boas* helper, int key)
{
  
    // If key is greater then universe_size then
    // returns false
    if (key >= helper->universe_size)
        return false;
  
    // If we reach at base case
    // the just return whether
    // pointer is nullptr then false
    // else return true
    if (helper->universe_size == 2) {
        return helper->clusters[key];
    }
    else {
  
        // Recursively go deep into the
        // level of Proto-VEB tree using its
        // cluster index and its position
        return isMember(helper->clusters[helper->high(key)],
                        helper->low(key));
    }
}
  
// Function to insert a key in the tree
void insert(Proto_Van_Emde_Boas*& helper, int key)
{
    // If we reach at base case
    // then assign Proto-VEB(1) in place
    // of nullptr
    if (helper->universe_size == 2) {
        helper->clusters[key] = new Proto_Van_Emde_Boas(1);
    }
    else {
  
        // Recursively using index of cluster and its
        // position in cluster
        insert(helper->clusters[helper->high(key)],
               helper->low(key));
  
        // Also do the same recusion in summary VEB
        insert(helper->summary, helper->high(key));
    }
}
  
// Function to return the minimum key from the tree
int minimum(Proto_Van_Emde_Boas* helper)
{
    // Base case chooses the least key
    // present in the cluster
    if (helper->universe_size == 2) {
        if (helper->clusters[0]) {
            return 0;
        }
        else if (helper->clusters[1]) {
            return 1;
        }
  
        // No keys present then return -1
        return -1;
    }
    else {
  
        // Recursively find in summary for
        // first 1 present in Proto-VEB
        int minimum_cluster = minimum(helper->summary);
        int offset;
  
        // If no key is present in
        // the cluster then return -1
        if (minimum_cluster == -1) {
            return -1;
        }
        else {
  
            // Recursively find the position of the key
            // in the minimum_cluster
            offset = minimum(helper->clusters[minimum_cluster]);
  
            // Returns overall index of minimum key
            return helper->generate_index(minimum_cluster, offset);
        }
    }
}
  
// Function to return the maximum key from the tree
int maximum(Proto_Van_Emde_Boas* helper)
{
  
    // Return the maximum key present in
    // the cluster
    if (helper->universe_size == 2) {
        if (helper->clusters[1]) {
            return 1;
        }
        else if (helper->clusters[0]) {
            return 0;
        }
  
        // Return -1 if no keys present in the
        // cluster
        return -1;
    }
    else {
  
        // Recursively find the last 1 present
        // in the summary
        int maximum_cluster = maximum(helper->summary);
        int offset;
  
        // If no key is present in
        // the cluster then return -1
        if (maximum_cluster == -1) {
            return -1;
        }
        else {
  
            // Recursively find the position of the key
            // in the maximum_cluster
            offset = maximum(helper->clusters[maximum_cluster]);
            return helper->generate_index(maximum_cluster, offset);
        }
    }
}
  
// Function to return the successor of key in the tree
int successor(Proto_Van_Emde_Boas* helper, int key)
{
    // Base case, returns key greater than
    // our query key in the cluster if present
    // else returns -1
    if (helper->universe_size == 2) {
        if (key == 0 && helper->clusters[1])
            return 1;
        else
            return -1;
    }
    else {
  
        // Check if any key is greater than query key in the cluster
        int offset = successor(helper->clusters[helper->high(key)],
                               helper->low(key));
  
        // If it is present then return its index
        if (offset != -1)
            return helper->generate_index(helper->high(key), offset);
        else {
  
            // If no successor is present within the cluster then
            // go to the summmary and find the next summary with
            // key present(1) named successor_cluster
            int successor_cluster = successor(helper->summary,
                                              helper->high(key));
  
            // If no next 1 in the summary then return -1
            if (successor_cluster == -1)
                return -1;
            else {
  
                // Find the minimum key in the successor_cluster
                offset = minimum(helper->clusters[successor_cluster]);
  
                // Generate its index and return
                return helper->generate_index(successor_cluster, offset);
            }
        }
    }
}
  
// Function to return the predecessor of key in the tree
int predecessor(Proto_Van_Emde_Boas* helper, int key)
{
  
    // Base case, find smaller key present in
    // the cluster
    // If present else return -1
    if (helper->universe_size == 2) {
        if (key == 1 && helper->clusters[0])
            return 0;
        else
            return -1;
    }
    else {
  
        // Check if any key is lower than query key in the cluster
        int offset = predecessor(helper->clusters[helper->high(key)],
                                 helper->low(key));
  
        // If it is present then return its index
        if (offset != -1)
            return helper->generate_index(helper->high(key), offset);
        else {
  
            // If no predecessor is present within the cluster then
            // go to the summmary and find the next summary with
            // key present(1) named predecessor_cluster
            int predecessor_cluster = predecessor(helper->summary,
                                                  helper->high(key));
  
            // If no next 1 in the summary then return -1
            if (predecessor_cluster == -1)
                return -1;
            else {
  
                // Find the maximum key in the predecessor_cluster
                offset = maximum(helper->clusters[predecessor_cluster]);
  
                // Generate its index and return
                return helper->generate_index(predecessor_cluster, offset);
            }
        }
    }
}
  
// Function to delete a key from the tree
void pveb_delete(Proto_Van_Emde_Boas*& helper, int key)
{
  
    // Base case: If the key is present
    // then make it nullptr
    if (helper->universe_size == 2) {
        if (helper->clusters[key]) {
            delete helper->clusters[key];
            helper->clusters[key] = nullptr;
        }
    }
    else {
  
        // Recursive delete to reach at the base case
        pveb_delete(helper->clusters[helper->high(key)], helper->low(key));
  
        bool isanyinCluster = false;
  
        // Iterate over the cluster of keys to check whether
        // any other key is present within that cluster
        // If yes then we should not update summary to 0
        // else update summary to 0
        for (int i = helper->high(key) * helper->root(helper->universe_size);
             i < (helper->high(key) + 1) * helper->root(helper->universe_size);
             i++) {
  
            // If member is present then break the loop
            if (isMember(helper->clusters[helper->high(key)], i)) {
                isanyinCluster = true;
                break;
            }
        }
  
        // If no member is present then
        // update summary to zero
        if (isanyinCluster == false) {
            pveb_delete(helper->summary, helper->high(key));
        }
    }
}
  
// Driver code
int main()
{
    Proto_Van_Emde_Boas* hello = new Proto_Van_Emde_Boas(16);
  
    cout << boolalpha;
  
    insert(hello, 2);
  
    insert(hello, 13);
  
    insert(hello, 3);
  
    cout << successor(hello, 3) << endl;
  
    cout << predecessor(hello, 13) << endl;
}

Отношение повторения для запросов преемника и предшественника:

 Т (и) = Т (и) = 2Т (  )) + O (log2 (  ))

Сложность времени: O (log2 (u) * log2 (log2 (u)))

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Структуры данных Продвинутая компьютерная тематика

Дерево Прото Ван Эмде Боас | Набор 6 | Запрос: преемник и предшественник

РЕКОМЕНДУЕМЫЕ СТАТЬИ