Алгоритмы цифровой обработки изображений с использованием MATLAB
Как говорится: «Одно изображение стоит больше, чем десять тысяч слов». Цифровое изображение состоит из тысяч и тысяч пикселей.
Изображение также можно определить как двумерную функцию f(x, y), где x и y — пространственные (плоские) координаты, поэтому амплитуда f в любой паре координат (x, y) называется интенсивностью. или уровень серого изображения в это время. Когда x, y и, следовательно, значения амплитуды f являются конечными дискретными величинами, мы называем изображение цифровым изображением.
Сегментация изображения с использованием различных методов
1. Базовые фильтры (маски):
Следующие фильтры используются для обнаружения краев и разрывов изображения.
Операторы первой производной:
- Маска Собеля — также используется для обнаружения двух видов краев на изображении: одного по вертикали, а другого по горизонтали.
- Маска Превитта — она также используется для обнаружения двух типов краев на изображении: горизонтальных и вертикальных краев. Края рассчитываются с использованием разницы между интенсивностью соответствующих пикселей изображения.
- Маска Роберта - используется для обнаружения краев путем аппроксимации градиента изображения посредством дискретного дифференцирования.
Операторы второй производной:
- Лапласиан — используется для поиска областей быстрого изменения (краев) изображений.
- Маска LOG (лапласиана гауссиана) (σ = 3). Поскольку производные фильтры очень чувствительны к шуму, перед применением лапласиана обычно сглаживают изображение (используя гауссовский фильтр). Этот двухэтапный процесс называется операцией Лапласа Гаусса (LoG).
- Детектор краев Canny — это популярный алгоритм обнаружения краев, который является многоэтапным и дает наилучшие результаты по сравнению с другими алгоритмами.
Градиентный метод, такой как метод Превитта, имеет самый важный недостаток — он чувствителен к шуму. Детектор границ Кэнни менее чувствителен к шуму, но дороже, чем детектор Роберта, Собеля и Превитта. Однако детектор краев Canny работает лучше, чем все маски.
Применение маски Собеля:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply Sobel Operator% Display only the horizontal Edgessobelhz = edge(myimage,"sobel","horizontal");subplot(3,3,2); imshow(sobelhz,[]); title("Sobel - Horizontal Edges"); % Apply Sobel Operator% Display only the vertical Edgessobelvrt = edge(myimage,"sobel","vertical");subplot(3,3,3); imshow(sobelhz,[]); title("Sobel - Vertical Edges"); % Apply Sobel Operator% Display both horizontal and vertical Edgessobelvrthz = edge(myimage,"sobel","both");subplot(3,3,4); imshow(sobelvrthz,[]); title("Sobel - All edges"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:



Применение маски Превитта:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply Prewitt Operator% Display both horizontal and vertical EdgesPrewittsedg = edge(myimage,"prewitt");subplot(3,3,6); imshow(Prewittsedg,[]); title("Prewitt - Edges"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

Применение Роберта Маска:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply Roberts Operator% Display both horizontal and vertical Edgesrobertsedg = edge(myimage,"roberts");subplot(3,3,5); imshow(robertsedg,[]); title("Roberts - Edges"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

Применение лапласианской маски:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply Laplacian Filter f=fspecial("laplacian"); lapedg = imfilter(myimage,f,"symmetric"); subplot(3,3,7); imshow(lapedg,[]); title("Laplacian Filter"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

Применение маски LOG:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply LOG edge detection % The sigma used is 3 f=fspecial("log",[15,15],3.0);logedg1 = edge(myimage,"zerocross",[],f);subplot(3,3,8); imshow(logedg1); title("Log with sigma 3"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:
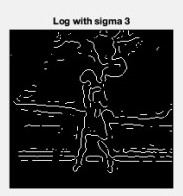
Применение детектора границ Canny:
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imagemycolourimage = imread("image1.jpg");myimage = rgb2gray(mycolourimage);subplot(3,3,1); imshow(myimage); title("Original Image"); % Apply Canny edge detection cannyedg = edge(myimage,"canny");subplot(3,3,9); imshow(cannyedg,[]); title("Canny Edge"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

Canny Edge Detector дает наилучшие результаты по сравнению с другими фильтрами/масками, используемыми для обнаружения краев на изображении.
2. Круговое преобразование Хафа:
Это глобальная обработка и специализация Hough Transform. Он используется для обнаружения кругов на входном изображении. Это преобразование выборочно для кругов и игнорирует вытянутые эллипсы.
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Image% Read the image that have circlesi=imread("image14.jpg"); % show imageimshow(i) % select max & min threshold of circles we want to detectRmin = 10Rmax = 50; % Apply Hough circular transform[centersDark1, radiiDark1] = imfindcircles(i, [Rmin Rmax],"ObjectPolarity","dark","Sensitivity",0.92); % show the detected circles by Red color --viscircles(centersDark1, radiiDark1,"LineStyle","--") |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:
3. Выбор порога:
Это локальный метод пороговой обработки, в котором мы локально устанавливаем входное изображение, передавая некоторые параметры. Мы взяли изображение, которое уже обработано по краю.
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original Imageimage = imread("image2.jpeg"); mean_image = imfilter(image, fspecial("average",[15,15]),"replica");subtract = image - (mean_image+20);black_white = im2bw(subtract,0);subplot(1,2,1); imshow(black_white); title("Threshold Image");subplot(1,2,2); imshow(image); title("Original Image"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

4. Метод Оцу:
Это метод оптимальной глобальной пороговой обработки. Otsu дает наилучший результат по сравнению с выбором порога при локальном определении порога. Этот метод минимизирует взвешенную внутриклассовую дисперсию.
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original ImageI1=imread("image2.jpeg"); %I1=rgb2gray(I);imshow(I1);figure, imhist(I1);T2 = graythresh(I1);it2= im2bw(I1,T2);figure,imshow(it2); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:

Изображение глобального порога
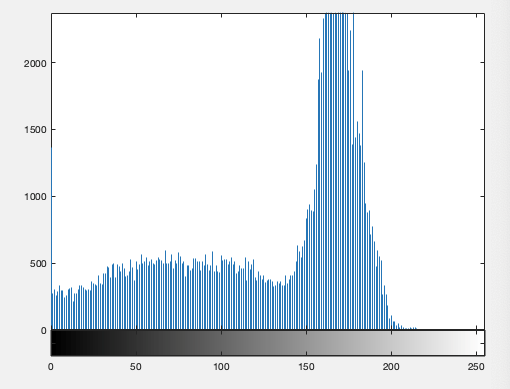
Гистограмма изображения
5. Морфологический водораздел:
При этом локальные минимумы уровней серого определяют водосборные бассейны, а локальные максимумы определяют линии водоразделов. В выходном изображении легко обнаружить маркеры.
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image% Display the original ImageI= imread("image10.png"); %I rgb2gray(RGB);I1 = imtophat(I, strel("disk", 10));figure, imshow(I1);I2 = imadjust(I1);figure,imshow(I2);level = graythresh(I2);BW = im2bw(I2,level);figure,imshow(BW);C=~BW;figure,imshow(C);D = ~bwdist(C);D(C) = -Inf;L = watershed(D);Wi=label2rgb(L,"hot","w");figure,imshow(Wi);im=I; |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:




6. Кластеризация K-средних:
Это алгоритм, который используется для отделения области интереса от фона. Разделите точки данных на K кластеров случайным образом. Найдите центроиды каждого кластера.
Он работает с двумерным массивом, где пиксели расположены в строках, а RGB — в столбцах. Мы берем средние значения для каждого класса (K=3).
Вход:
Код:
MATLAB
clc;close all;clear all; % Read Colour Image and convert it to a grey level Image % Load in an input imageim = imread("image12.png"); % We also cast to a double array, because K-means requires it in matlabimflat = double(reshape(im, size(im,1) * size(im,2), 3));K = 3[kIDs, kC] = kmeans(imflat, K, "Display", "iter", "MaxIter", 150, "Start", "sample");colormap = kC / 256; % Scale 0-1, since this is what matlab wants% Reshape kIDs back into the original image shapeimout = reshape(uint8(kIDs), size(im,1), size(im,2));imwrite(imout - 1, colormap, "image6.jpg"); |
Вызовите вышеуказанную функцию с помощью командного окна MATLAB.
Выход:
K =
3
iter phase num sum
1 1 178888 1.52491e+08
2 1 7657 1.45223e+08
3 1 4597 1.42317e+08
4 1 3750 1.40017e+08
5 1 3034 1.38203e+08
6 1 2187 1.37096e+08
7 1 1552 1.36481e+08
8 1 1044 1.36165e+08
9 1 701 1.36014e+08
10 1 479 1.35939e+08
11 1 311 1.35906e+08
12 1 282 1.35883e+08
13 1 193 1.3587e+08
14 1 124 1.35865e+08
15 1 85 1.35863e+08
16 1 60 1.35861e+08
17 1 80 1.3586e+08
18 1 79 1.35858e+08
19 1 23 1.35858e+08
20 1 48 1.35858e+08
21 1 7 1.35858e+08
Best total sum of distances = 1.35858e+08