Алгоритм Шеннона-Фано для сжатия данных

Опубликовано: 3 Декабря, 2021

СЖАТИЕ ДАННЫХ И ЕЕ ВИДЫ
Сжатие данных, также известное как исходное кодирование, - это процесс кодирования или преобразования данных таким образом, чтобы он потреблял меньше места в памяти. Сжатие данных уменьшает количество ресурсов, необходимых для хранения и передачи данных.
Это можно сделать двумя способами: сжатие без потерь и сжатие с потерями. Сжатие с потерями уменьшает размер данных за счет удаления ненужной информации, в то время как при сжатии без потерь данные отсутствуют.

ЧТО ТАКОЕ FANO CODING SHANNON?
Алгоритм Шеннона Фано - это метод энтропийного кодирования для сжатия мультимедийных данных без потерь. Названный в честь Клода Шеннона и Роберта Фано, он присваивает код каждому символу в зависимости от вероятности их появления. Это схема кодирования переменной длины, то есть коды, присвоенные символам, будут иметь разную длину.

КАК ЭТО РАБОТАЕТ?
Шаги алгоритма следующие:

Создайте список вероятностей или значений частоты для данного набора символов, чтобы известна относительная частота встречаемости каждого символа.
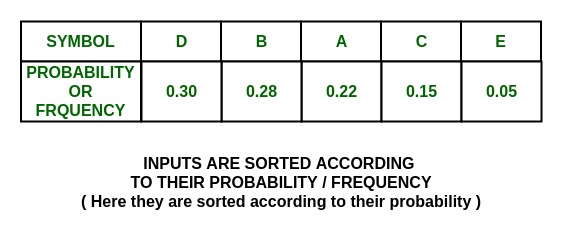
Отсортируйте список символов в порядке убывания вероятности, наиболее вероятные слева и наименее вероятные справа.
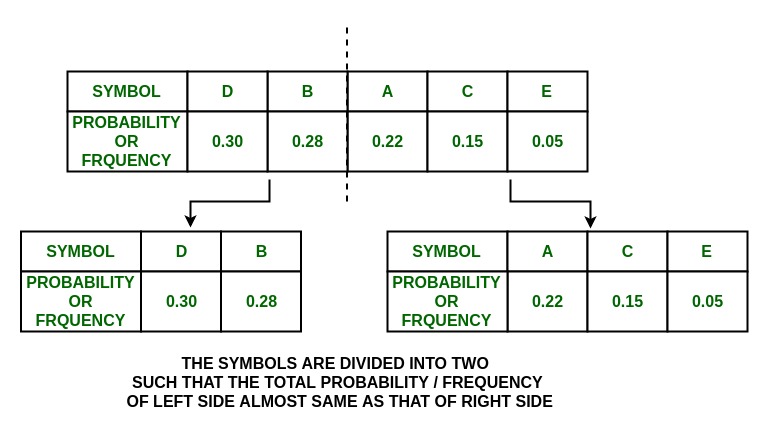
Разделите список на две части, с полной вероятностью того, что обе части будут как можно ближе друг к другу.
Присвойте значение 0 левой части и 1 - правой части.
Повторите шаги 3 и 4 для каждой части, пока все символы не будут разделены на отдельные подгруппы.

Коды Шеннона считаются точными, если код каждого символа уникален.

ПРИМЕР:
Данная задача состоит в построении кодов Шеннона для заданного набора символов с использованием техники сжатия Шеннона-Фано без потерь.

Шаг:

Дерево: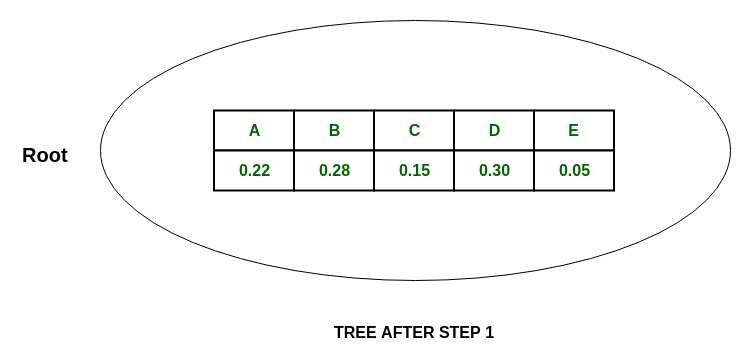

Решение:

После расположения символов в порядке убывания вероятности:
P(D) + P(B) = 0.30 + 0.2 = 0.58
а также,
P(A) + P(C) + P(E) = 0.22 + 0.15 + 0.05 = 0.42
И так как таблица разделена почти поровну, большая часть таблицы цитат разделена на блоки.

{D, B} and {A, C, E}
и присвоить им значения 0 и 1 соответственно.
Шаг:

Дерево:
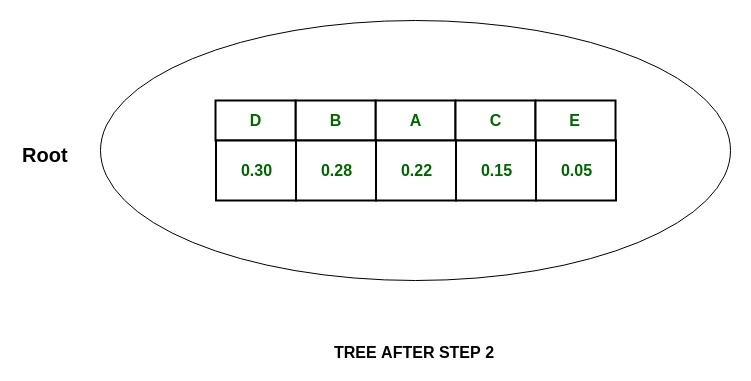
Теперь в группе {D, B},
P(D) = 0.30 and P(B) = 0.28
что означает, что P (D) ~ P (B) , поэтому разделите {D, B} на {D} и {B} и присвойте 0 D и 1 B.
Шаг:

Дерево:
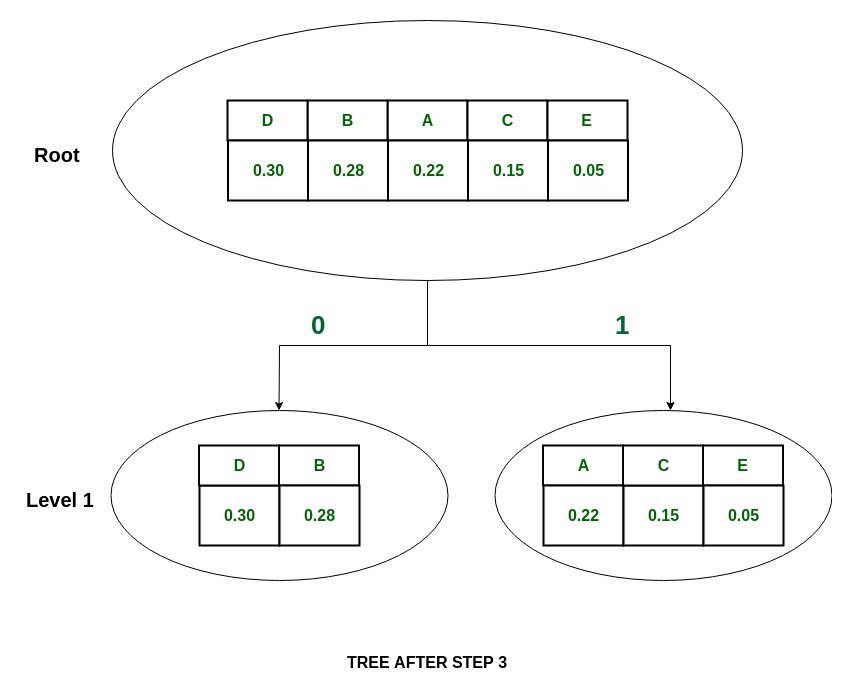
В группе {A, C, E}
P(A) = 0.22 and P(C) + P(E) = 0.20
Итак, группа делится на
{A} and {C, E}
и им присваиваются значения 0 и 1 соответственно.
В группе {C, E}
P(C) = 0.15 and P(E) = 0.05
Разделите их на {C} и {E} и присвойте 0 {C} и 1 {E}
Шаг:

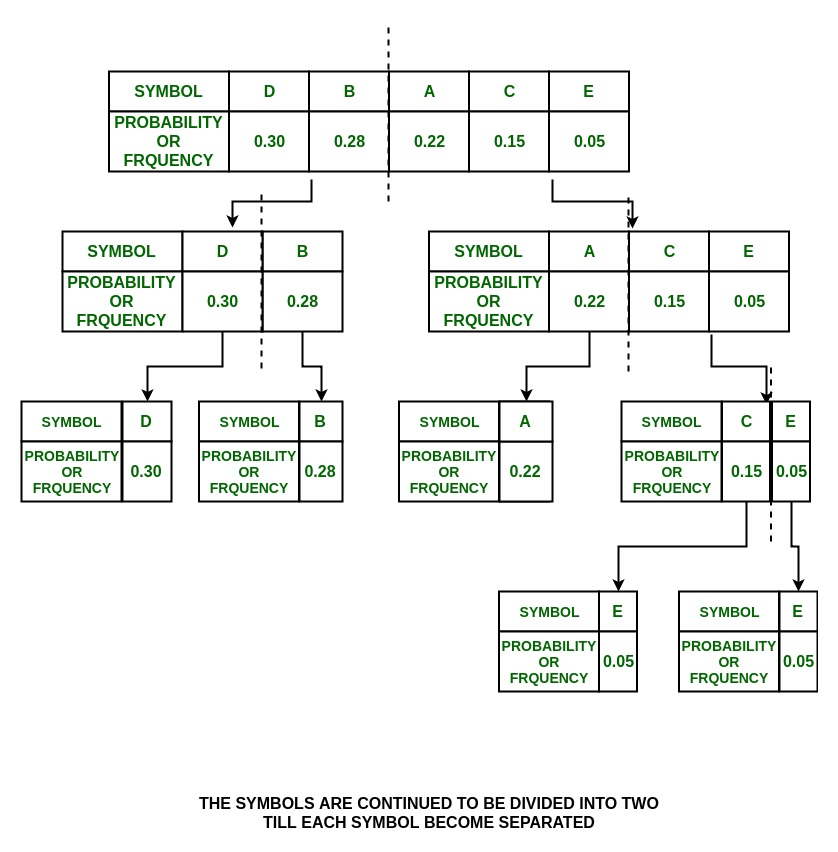
Дерево:
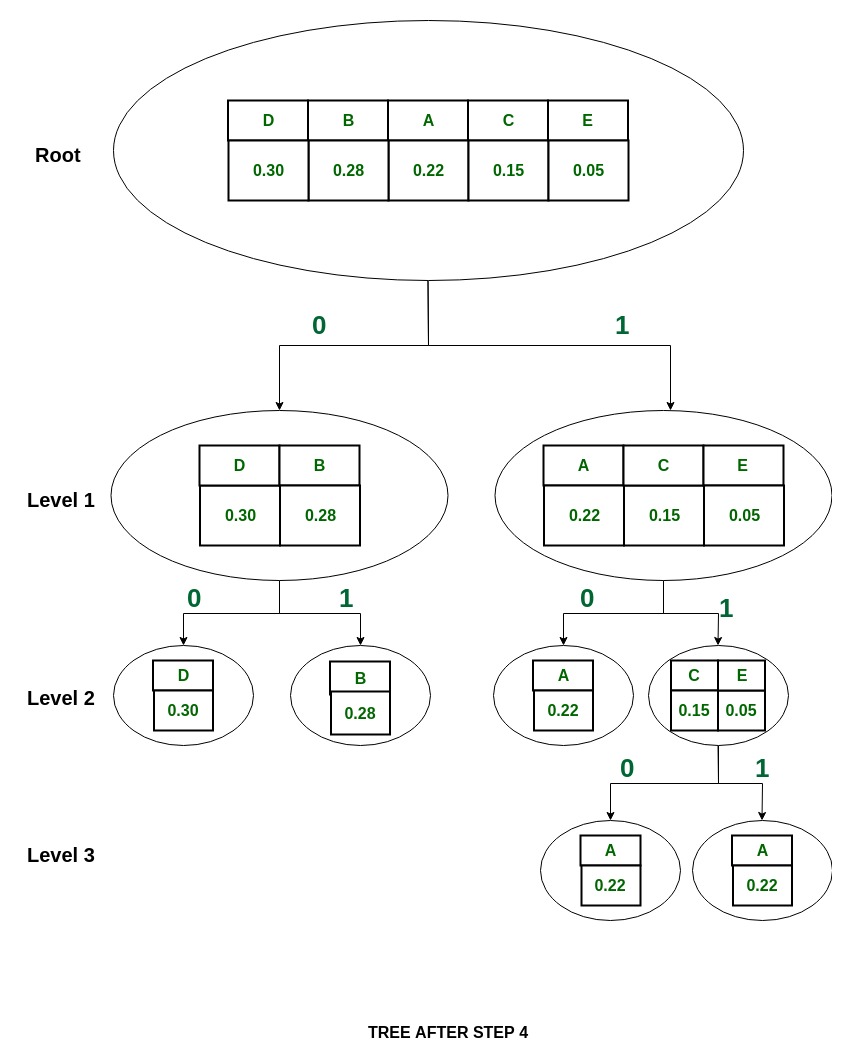
Примечание: теперь разделение остановлено, так как теперь каждый символ отделен.

Коды Шеннона для набора символов: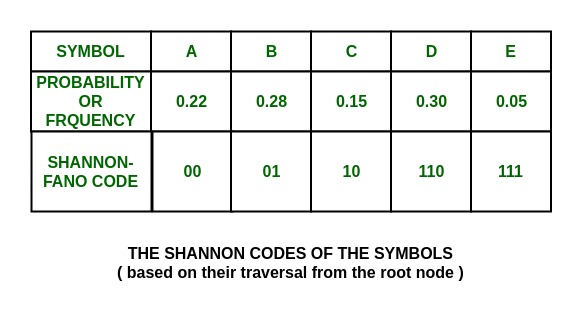

Как видно, все они уникальны и разной длины.

Ниже представлена реализация описанного выше подхода:

 // C++ program for Shannon Fano Algorithm
 
// include header files
 #include <bits/stdc++.h>
 using namespace std;
 
// declare structure node
 struct node {
 
    // for storing symbol
    string sym;
 
    // for storing probability or frquency
    float pro;
    int arr[20];
    int top;
 } p[20];
 
typedef struct node node;
 
// function to find shannon code
 void shannon( int l, int h, node p[])
 {
    float pack1 = 0, pack2 = 0, diff1 = 0, diff2 = 0;
    int i, d, k, j;
    if ((l + 1) == h || l == h || l > h) {
        if (l == h || l > h)
            return ;
        p[h].arr[++(p[h].top)] = 0;
        p[l].arr[++(p[l].top)] = 1;
        return ;
    }
    else {
        for (i = l; i <= h - 1; i++)
            pack1 = pack1 + p[i].pro;
        pack2 = pack2 + p[h].pro;
        diff1 = pack1 - pack2;
        if (diff1 < 0)
            diff1 = diff1 * -1;
        j = 2;
        while (j != h - l + 1) {
            k = h - j;
            pack1 = pack2 = 0;
            for (i = l; i <= k; i++)
                pack1 = pack1 + p[i].pro;
            for (i = h; i > k; i--)
                pack2 = pack2 + p[i].pro;
            diff2 = pack1 - pack2;
            if (diff2 < 0)
                diff2 = diff2 * -1;
            if (diff2 >= diff1)
                break ;
            diff1 = diff2;
            j++;
        }
        k++;
        for (i = l; i <= k; i++)
            p[i].arr[++(p[i].top)] = 1;
        for (i = k + 1; i <= h; i++)
            p[i].arr[++(p[i].top)] = 0;
 
        // Invoke shannon function
        shannon(l, k, p);
        shannon(k + 1, h, p);
    }
 }
 
// Function to sort the symbols
 // based on their probability or frequency
 void sortByProbability( int n, node p[])
 {
    int i, j;
    node temp;
    for (j = 1; j <= n - 1; j++) {
        for (i = 0; i < n - 1; i++) {
            if ((p[i].pro) > (p[i + 1].pro)) {
                temp.pro = p[i].pro;
                temp.sym = p[i].sym;
 
                p[i].pro = p[i + 1].pro;
                p[i].sym = p[i + 1].sym;
 
                p[i + 1].pro = temp.pro;
                p[i + 1].sym = temp.sym;
            }
        }
    }
 }
 
// function to display shannon codes
 void display( int n, node p[])
 {
    int i, j;
    cout << "


	Symbol	Probability	Code" ;
    for (i = n - 1; i >= 0; i--) {
        cout << "
	" << p[i].sym << "		" << p[i].pro << "	" ;
        for (j = 0; j <= p[i].top; j++)
            cout << p[i].arr[j];
    }
 }
 
// Driver code
 int main()
 {
    int n, i, j;
    float total = 0;
    string ch;
    node temp;
 
    // Input number of symbols
    cout << "Enter number of symbols	: " ;
    n = 5;
    cout << n << endl;
 
    // Input symbols
    for (i = 0; i < n; i++) {
        cout << "Enter symbol " << i + 1 << " : " ;
        ch = ( char )(65 + i);
        cout << ch << endl;
 
        // Insert the symbol to node
        p[i].sym += ch;
    }
 
    // Input probability of symbols
    float x[] = { 0.22, 0.28, 0.15, 0.30, 0.05 };
    for (i = 0; i < n; i++) {
        cout << "
Enter probability of " << p[i].sym << " : " ;
        cout << x[i] << endl;
 
        // Insert the value to node
        p[i].pro = x[i];
        total = total + p[i].pro;
 
        // checking max probability
        if (total > 1) {
            cout << "Invalid. Enter new values" ;
            total = total - p[i].pro;
            i--;
        }
    }
 
    p[i].pro = 1 - total;
 
    // Sorting the symbols based on
    // their probability or frequency
    sortByProbability(n, p);
 
    for (i = 0; i < n; i++)
        p[i].top = -1;
 
    // Find the shannon code
    shannon(0, n - 1, p);
 
    // Display the codes
    display(n, p);
    return 0;
 }

Выход:

Введите количество символов: 5
Введите символ 1: A
Введите символ 2: B
Введите символ 3: C
Введите символ 4: D
Введите символ 5: E

Введите вероятность A: 0,22

Введите вероятность B: 0,28

Введите вероятность C: 0,15

Введите вероятность D: 0,3

Введите вероятность E: 0,05



    Код вероятности символа
    Д 0,3 00
    В 0,28 01
    А 0,22 10
    С 0,15 110
    E 0,05 111

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по доступной для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Technical Scripter Компьютерные сети Алгоритмы

Алгоритм Шеннона-Фано для сжатия данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ