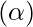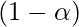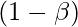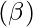Альфа и бета тест

Опубликовано: 17 Июля, 2021

В предыдущей статье мы обсуждали проверку гипотез, которая является основой выводимой статистики. Ранее мы обсуждали основную проверку гипотез, включая нулевую и альтернативную гипотезы, z-тест и т. Д. Теперь в этом разделе обсуждались дополнительные ошибки типа I и типа II, уровень значимости (альфа) и степень (бета).

P-значение:

Значение p определяется как вероятность получения результата или более экстремального, чем то, что на самом деле наблюдалось при нормальном распределении. Обычно мы принимаем уровень значимости = 0,05, это означает, что если наблюдаемое значение p меньше уровня значимости, то мы отклоняем нулевую гипотезу.

Чтобы вычислить p-значение, нам нужна таблица конкретной статистики теста (t-тест, z-тест, f-тест) и является ли это односторонним, двусторонним тестом.

p-значение

Альфа- и бета-тест:

	Нулевая гипотеза верна	Нулевая гипотеза ЛОЖНА
Отклонить нулевую гипотезу	Ошибка типа I	Правильное решение
Неспособность отвергнуть нулевую гипотезу	Правильное решение	Ошибка типа II

Ошибка типа I (альфа): теперь, если мы отклоняем нулевую гипотезу на основе вычислений уровня значимости p-значения, существует вероятность того, что выборки в действительности принадлежат одному (нулевому) распределению, и мы ошибочно отклонили это называется ошибкой типа I и обозначается буквой альфа.
Ошибка типа II (бета) : теперь, на основе уровня значимости и p-значения, если мы принимаем образец, который на самом деле не принадлежит к тому же распределению, тогда это называется ошибкой типа II.

Интервал силы и уверенности:

Доверительный интервал: доверительный интервал - это область, в которой мы можем уверенно отклонить нулевую гипотезу. Он рассчитывается путем вычитания альфы и 1.

Власть : Власть - это вероятность правильного отклонения нулевой гипотезы и принятия альтернативной гипотезы (H _A ). Мощность может быть рассчитана путем вычитания бета из 1.

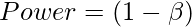
Чем выше мощность, тем ниже вероятность ошибки типа II. Меньшая мощность означает более высокий риск возникновения ошибки типа II и наоборот. Как правило, мощность 0,80 считается достаточно хорошей. Мощность также зависит от следующих факторов:

Размер эффекта: Размер эффекта - это просто способ измерения силы взаимосвязи между двумя переменными. Существует множество способов вычисления величины эффекта, например, корреляции Пирсона для вычисления корреляций между двумя переменными, d-критерий Коэна для измерения разницы между группами или просто вычисление разницы между средними значениями разных групп.
Размер выборки: количество наблюдений, включенных в статистическую выборку.
Значимость : уровень значимости, использованный в тесте (альфа).

Шаги по выполнению анализа мощности

Сформулируйте нулевую гипотезу (H ₀ ) и альтернативную гипотезу (H _A ).
Укажите уровень альфа-риска (уровень значимости).
Выберите подходящий статистический тест.
Определите размер эффекта.
Составьте планы выборки и определите размер выборки. После этого соберите образец.
Рассчитайте статистику теста, определив p-значение.
- Если p-значение <альфа, то мы отклоняем нулевую гипотезу.
Повторите вышеуказанные шаги несколько раз.

Примеры

Распределение специальной диеты против нормального распределения

Предположим, есть два распределения, представляющие веса двух групп людей, левая часть представляет людей, сидящих на диете, а правая - людей, которые принимают обычную пищу.
Мы берем несколько выборок из обоих распределений и вычисляем их средние.
Здесь наша нулевая гипотеза будет заключаться в том, что обе выборки относятся к одному и тому же распределению (без эффекта от плана диеты), а альтернативная гипотеза будет заключаться в том, что обе выборки относятся к разному распределению.
Теперь мы вычисляем p-значение из этих выборок.
Если наше значение p меньше уровня значимости, то мы правильно отклоняем нулевую гипотезу о том, что обе эти выборки принадлежат к одному и тому же распределению.
иначе мы не отвергаем нулевую гипотезу.
Теперь мы повторяем вышеуказанные шаги несколько раз (например, 1000, 10000) и т. Д. И вычисляем вероятность правильного отклонения нулевой гипотезы, то есть мощности.

Выполнение:

Python3

 # Necessary Imports
 import numpy as np
 from statsmodels.stats.power import TTestIndPower
 import matplotlib.pyplot as plt
 
# here effect size is taken as (u1-u2) /sd
 effect_size = ( 60 - 50 ) / 10
 alpha = 0.05
 samples = 20
 p_analysis = TTestIndPower()
 power = p_analysis.solve_power(effect_size = effect_size, alpha = alpha, nobs1 = samples, ratio = 1 )
 print ( "Power is " ,power) 

 0,8689530131730794

Машинное обучение