5 переменных K-Map в Digital Logic

Предварительное условие - Участие в K-Map
Карта Карно или K-карта - это альтернативный способ записи таблицы истинности, который используется для упрощения логических выражений. Пока мы знакомы с 3-х переменными K-Map и 4-х переменными K-Map. Теперь давайте подробно обсудим 5-переменную K-карту.

Любое логическое выражение или функция, состоящая из 5 переменных, может быть решена с помощью 5 переменных K-Map. Такая 5-переменная K-карта должна содержать 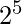= 32 ячейки . Пусть булева функция с 5 переменными будет представлена как:
f (PQRST), где P, Q, R, S, T - переменные, P - старшая битовая переменная, а T - младшая битовая переменная.

Структура такой K-карты для выражения SOP приведена ниже:

Ячейки нет. написанное, соответствующее каждой ячейке, можно понять из примера, описанного здесь: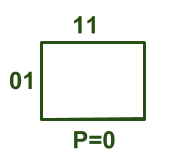

Здесь для переменной P = 0 мы имеем Q = 0, R = 1, S = 1, T = 1, т.е. (PQRST) = (00111) . В десятичной форме это эквивалентно 7 . Итак, для ячейки, показанной выше, соответствующая ячейка № = 7. Аналогичным образом мы можем записать номера ячеек, соответствующие каждой ячейке, как показано на рисунке выше.
Теперь давайте обсудим, как использовать 5 переменных K-Map для минимизации логической функции.

Правила, которых необходимо придерживаться:

1. Если функция задана в компактной канонической форме SOP (Sum of Products), то мы пишем «1», соответствующую каждому minterm (указанному в вопросе) в соответствующих номерах ячеек. Например:
   Для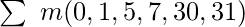 мы напишем «1» в соответствии с номерами ячеек (0, 1, 5, 7, 30 и 31).
2. Если функция задана в компактной канонической форме POS (произведение сумм), то мы пишем «0», соответствующий каждому maxterm (указанному в вопросе) в соответствующих номерах ячеек. Например:
   Для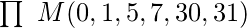 мы будем писать «0» в соответствии с номерами ячеек (0, 1, 5, 7, 30 и 31).

Действия, которые необходимо выполнить:

1. Сделайте подкуб максимально возможного размера, покрывающий все отмеченные единицы в случае SOP или все отмеченные 0 в случае POS на K-Map. Важно отметить, что каждый вложенный куб может содержать только члены со степенью 2. Также подкуб 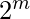ячеек возможен тогда и только тогда, когда в этом подкубе для каждой ячейки мы удовлетворяем, что количество ячеек «m» является соседними ячейками .
2. Все основные основные импликанты (EPI) должны присутствовать в минимальных выражениях.

I. Решение функции СОП -
Для ясного понимания, давайте решим пример минимизации функции SOP 5 переменных K-Map, используя следующее выражение: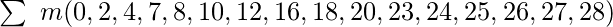

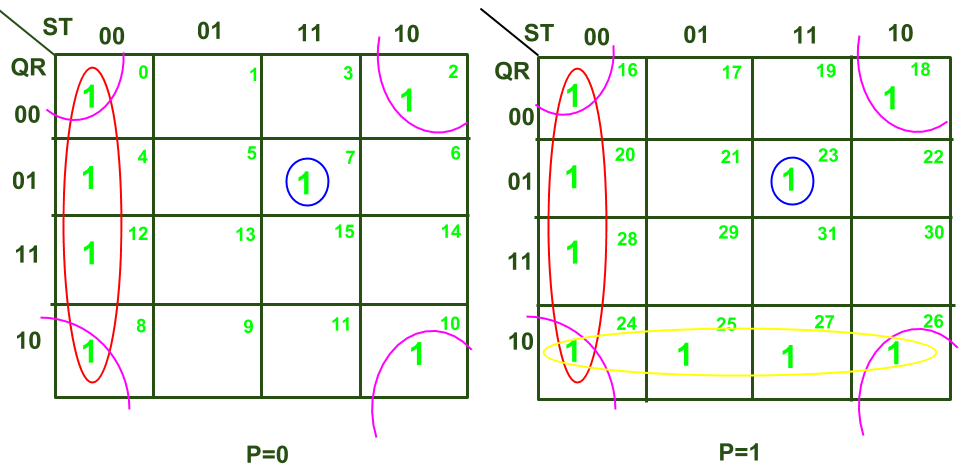
В приведенной выше K-Map у нас есть 4 субкуба:

• Подкуб 1: выделенный красным состоит из ячеек (0, 4, 8, 12, 16, 20, 24, 28).
• Подкуб 2: тот, что отмечен синим, состоит из ячеек (7, 23).
• Подкуб 3: выделенный розовым цветом состоит из ячеек (0, 2, 8, 10, 16, 18, 24, 26).
• Подкуб 4: тот, который отмечен желтым, состоит из ячеек (24, 25, 26, 27).

Теперь, при написании минимального выражения для каждого из вложенных кубов, мы будем искать литерал, который является общим для всех ячеек, присутствующих в этом вложенном кубе.

• Подкуб 1 :
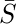
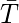
• Подкуб 2 :
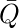
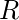
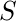
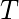
• Подкуб 3 :
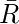
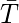
• Подкуб 4 :

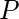
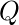
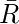
Наконец, минимальное выражение данной логической функции можно выразить следующим образом: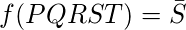

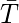
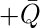
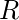
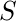
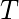
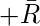
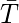
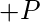
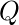
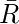
II. Решение POS-функции -
Теперь давайте решим пример минимизации функции POS для 5 переменных K-Map, используя следующее выражение: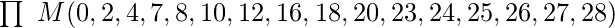

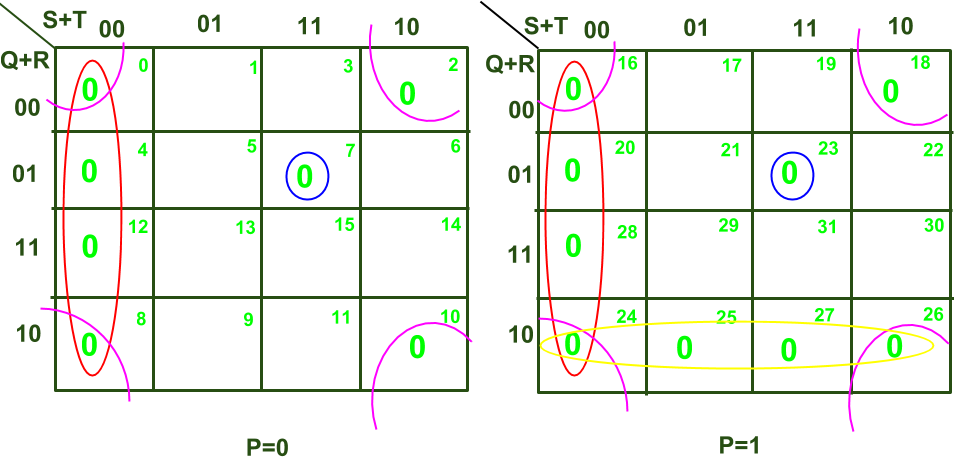
В приведенной выше K-Map у нас есть 4 субкуба:

• Подкуб 1: выделенный красным состоит из ячеек (0, 4, 8, 12, 16, 20, 24, 28).
• Подкуб 2: тот, что отмечен синим, состоит из ячеек (7, 23).
• Подкуб 3: выделенный розовым цветом состоит из ячеек (0, 2, 8, 10, 16, 18, 24, 26).
• Подкуб 4: тот, который отмечен желтым, состоит из ячеек (24, 25, 26, 27).

Теперь, при написании минимального выражения для каждого из вложенных кубов, мы будем искать литерал, который является общим для всех ячеек, присутствующих в этом вложенном кубе.

• Подкуб 1 :
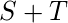
• Подкуб 2 :
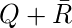
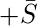
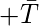
• Подкуб 3 :
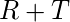
• Подкуб 4 :

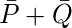
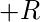
Наконец, минимальное выражение данной логической функции можно выразить следующим образом: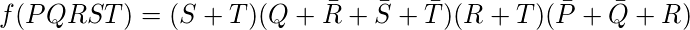

ПРИМЕЧАНИЕ :

1. Для 5 переменных K-Map диапазон номеров ячеек будет от 0 до 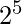-1 то есть от 0 до 31.
2. Вышеупомянутый термин «Смежные ячейки» означает «любые две ячейки, которые отличаются только одной переменной».