Задача коммивояжера Bitonic

Учитывая двумерный массив arr[][] , обозначающий список координат N вершин в двумерном пространстве, который уже отсортирован по координатам x и y, задача состоит в том, чтобы найти минимальное расстояние тура, который начинается с крайнего левого вершине, и идет строго вправо, а затем по достижении крайней правой вершины обход идет строго справа налево-назад к начальной вершине.

Примеры:

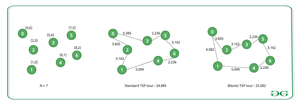
Input: N = 7, arr[][] = {{0, 6}, {1 0}, {2 3}, {5 4}, {6 1}, {7 5}, {8 2}}
Output: 25.582
Explanation: 

The TSP tour: 0-3-5-6-4-1-2-0 is not a Bitonic TSP tour because although the tour initially goes from left to right (0-3-5-6) and then goes back from right to left (6-4-1), it then makes another left to right (1-2) and then right to left (2-0) steps. 
The tour: 0-2-3-5-6-4-1-0 is a valid Bitonic TSP tour because it can be decomposed into two paths: 0-2-3-5-6 that goes from left to right and 6-4-1-0 that goes back from right to left.

Input: N = 3, arr[][] = {{1, 1}, {2, 3}, {3, 1}}
Output: 6.47

Подход: Вышеупомянутая проблема может быть решена с помощью динамического программирования. Для понимания задачу можно поменять на двух человек. Оба должны начинаться с крайней левой точки одновременно. Пройдите по двум разным путям и, наконец, доберитесь до крайней правой точки, за исключением начальной и конечной точек.

• Каждая точка проходится одним человеком. Здесь dp[i][j] представляет, как далеко первый человек проходит до i , а второй — до j .
• В решении dp[i][j] означает, что все от 1 до max(i, j) были пройдены, а текущие позиции двух людей равны i и j соответственно и то, как далеко им нужно пройти.
• Кроме того, можно сделать вывод, что dp[i][j] равно dp[j][i] , поэтому с этого момента оговаривается, что i всегда больше, чем j , т.е. i>j в состоянии.
• Таким образом, независимо от этого человека, следующий шаг может идти только к i+1, i+2,… этим точкам.
• Итак, состояние dp[i][j] может быть передано только в dp[i+1][j] или dp[i][i+1].

Выполните следующие шаги, чтобы решить проблему:

• Создайте двумерный массив dp[][] размера N*N .
• Повторите последнюю строку таблицы, dp , и обновите dp[N-1][i] до суммы расстояний(N-1, N) и расстояний(i, N) , где расстояние(x, y) представляет собой Евклидово расстояние между x -й и y -й точками обр .
• Создайте рекурсивную функцию findTour(i, j) для заполнения всех остальных ячеек
  • Обновите dp[i][j] до минимума findTour(i+1, j)+distance(i, i+1) и findTour(i+1, i)+distance(j, i+1) .

Ниже приведена реализация вышеуказанного подхода:

Временная сложность: O(N ² )
Вспомогательное пространство: O(N ² )