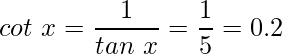Взаимность тригонометрических соотношений

Тригонометрия - это все о треугольниках, а точнее о соотношении между углами и сторонами прямоугольного треугольника. В этой статье мы обсудим отношение сторон прямоугольного треугольника к его острому углу, называемое тригонометрическими отношениями угла, и найдем обратные величины этим тригонометрическим отношениям.

Рассмотрим следующий треугольник:

Некоторые основные моменты, которые следует запомнить

• ∠XYZ называется просто ∠Y, например ACB называется просто ∠C
• Сторона, противоположная θ (θ - любой острый угол), называется стороной, противоположной θ.
• Сторона, примыкающая к θ, называется смежной стороной по отношению к ∠θ.
• Самая длинная сторона прямоугольного треугольника - гипотенуза.

Основные тригонометрические соотношения

Тригонометрические отношения острого угла в прямоугольном треугольнике - это соотношение между углом и длиной двух сторон. Здесь мы будем использовать угол C в △ ABC для определения всех тригонометрических соотношений. Определенные ниже отношения сокращенно обозначаются как sin C, cos C и tan C соответственно.

A. Синус: Синус ∠C - это отношение между BA и AC, которое представляет собой отношение между стороной, противоположной ∠C, и гипотенузой.

B. Косинус: косинус ∠C - это отношение между BC и AC, которое представляет собой отношение между стороной, прилегающей к ∠C, и гипотенузой.

C. Касательная: Касательная к ∠C - это отношение между BA и BC, то есть отношение между стороной, противоположной C, и прилегающей к ней.

Обратные тригонометрические отношения

Обратные величины основных тригонометрических соотношений - это значения, обратные значениям sin, cos и tan, которые вычисляются путем возвратно-поступательного движения сторон, необходимых для вычисления отношения. Вы увидите, что cosec A, sec A и cot A соответственно являются обратными величинами sin A, cos A и tan A из следующих диаграмм и примеров.

A. Взаимный грех C

Синус - это отношение противоположной стороны к гипотенузе. косеканс - это величина, обратная греху, то есть отношению гипотенузы к противоположной стороне.

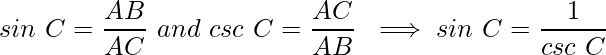
Пример 1: Если значение sin x = 0,47, то найти значение cosec x?

Решение: значение sin x = 0,47

а также

Пример 2: Если значение cosec C = 3, то найти значение sin C?

Решение: значение cosec C = 4

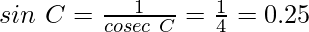
Б. Величина, обратная cos C

Cos - отношение соседней стороны к гипотенузе. Секущая - это величина, обратная cos, то есть отношению гипотенузы к прилегающей стороне.

Пример 1: Если значение cos x = 0, то найти значение sec x?

Решение: cos x = 0

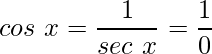
сек x не определен, так как деление на 0 невозможно

Пример 2: Если значение sec x = 100, найти значение cos x?

Решение: sec x = 100

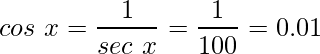
C. Взаимно с tan C

Загар - это отношение противоположной стороны к смежной стороне. Котангенс - это величина, обратная tan, то есть отношение между соседней стороной и противоположной стороной.

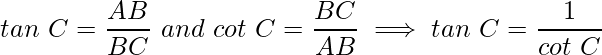
Пример 1: найти значение tan x и cot x, если x = 30 °?

Решение: x = 30 °

Пример 2: Если значение tan x = 5 найти значение cot x?

Решение: tan x = 5