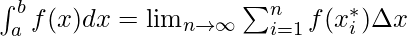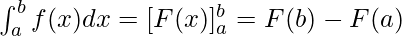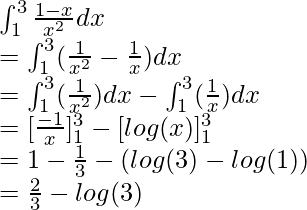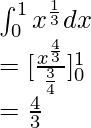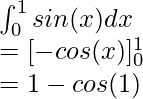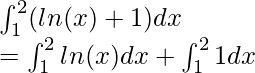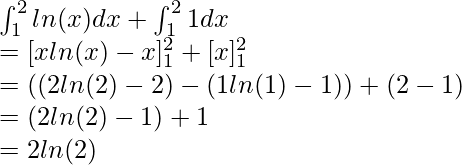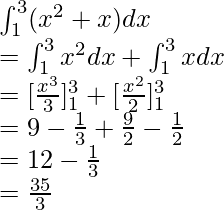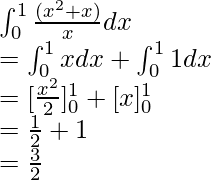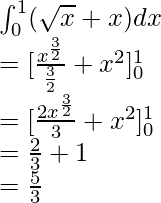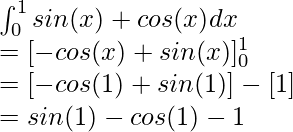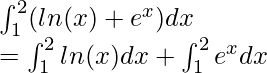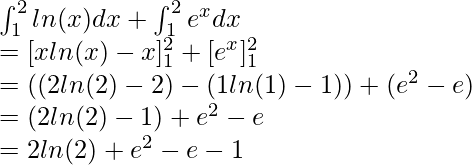Вычисление определенных интегралов
Интегралы являются очень важной частью исчисления. Они позволяют нам вычислять первообразные, то есть по заданной производной функции, интегралы дают функцию на выходе. Другие важные применения интегралов включают вычисление площади под кривой, объема, ограниченного поверхностью, и т. д. В то время как предыдущее приложение в основном включает неопределенные интегралы, последнее требует, чтобы границы были четко определены, и интеграл вычисляется между этими только границы. Такие интегралы называются определенными интегралами.
Определенные интегралы
Определенные интегралы в основном используются для вычисления площадей и объемов, ограниченных кривыми. Обычно площадь вычисляется по определенным формулам для прямоугольников, кругов, квадратов и т. д. В реальной жизни фигуры не так просты, поэтому для вычисления площадей любой произвольной формы мы используем определенные интегралы. Для функции f (x), определенной на интервале [a, b], определенный интеграл между этими пределами определяется выражением
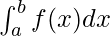
Здесь a называется нижним пределом функции, а b называется верхним пределом функции.
Given a function f(x) that is continuous on the interval [a, b] we divide the interval into n subintervals of equal width,
and from each interval choose a point
. Then the definite integral of f(x) from a to b is,

Приведенный выше рисунок объясняет определение предела: по мере того, как мы увеличиваем количество прямоугольников под кривой, аппроксимированная площадь становится все ближе и ближе к фактической площади под рисунком.
Основная теорема исчисления
Площадь области, ограниченной кривой f(x) между ординатами x = a и x = b и осью x, определяется выражением 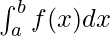 . Допустим, x - любая точка между пределами, тогда
. Допустим, x - любая точка между пределами, тогда 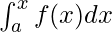 представляет собой площадь области от a до x. Другими словами, площадь этой заштрихованной области от «а» до значения х называется функцией площади. Это дается,
представляет собой площадь области от a до x. Другими словами, площадь этой заштрихованной области от «а» до значения х называется функцией площади. Это дается,
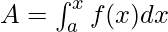

На основе этого определения сформулированы две основные теоремы исчисления.
Первая фундаментальная теорема исчисления
Let f(x) be a continuous function on the closed interval [a, b] and let A(x) be the area function.
Then, A"(x) = f(x), for all x ∈ [a, b].
Вторая фундаментальная теорема исчисления
Let f(x) be a continuous function on the closed interval [a, b] and let F(x) be the anti-derivatives of the function f(x). Then,
Площадь под кривой
Площадь под кривой определяется определенными интегралами. Мы знаем, что площадь всегда положительная величина, но при использовании определенных интегралов иногда площадь получается отрицательной. Например, рассмотрим две функции ниже: одна лежит полностью над осью абсцисс, а другая имеет некоторую часть, лежащую ниже оси абсцисс. В таких случаях две области могут компенсировать друг друга.

В этом случае площадь определяется как
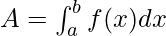

В этом случае отрицательную и положительную площади нужно вычислять отдельно и добавлять только величину их площадей.
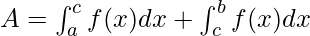
Определенные интегралы рациональной функции
Для вычисления определенных интегралов для таких функций эти функции разбиваются с помощью алгебраических операций.
Вопрос: Вычислите значение следующего интеграла
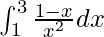
Решение:
Определенные интегралы радикальных функций
Для вычисления определенных интегралов таких функций воспользуемся правилом обратной степени.
Вопрос: Вычислите значение следующего интеграла
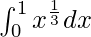
Решение:
Using the reversed power rule,
Определенные интегралы тригонометрических функций
Для вычисления определенных интегралов таких функций воспользуемся правилом обратной степени.
Вопрос: Вычислите значение следующего интеграла
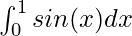
Решение:
Определенные интегралы натуральных логарифмических функций
Для вычисления определенных интегралов таких функций воспользуемся следующим тождеством.
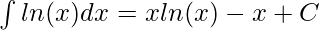
Вопрос: Вычислите значение следующего интеграла
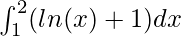
Решение:
Using the formula mentioned above,
Давайте посмотрим на некоторые примеры задач
Примеры проблем
Вопрос 1: Вычислите значение следующего интеграла
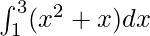
Решение:
Вопрос 2: Вычислите значение следующего интеграла
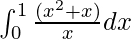
Решение:
Вопрос 3: Вычислите значение следующего интеграла
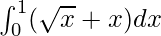
Решение:
Using the reversed power rule
Вопрос 4: Вычислите значение следующего интеграла
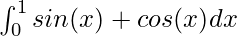
Решение:
Вопрос 5: Вычислите значение следующего интеграла
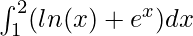
Решение:
Using the formula mentioned above,