Введение в NP-полноту

Мы писали об эффективных алгоритмах для решения сложных задач, таких как кратчайший путь, граф Эйлера, минимальное остовное дерево и т. д. Все это были истории успеха разработчиков алгоритмов. В этом посте обсуждаются неудачные истории информатики.

Может ли компьютер решить все вычислительные задачи? Существуют вычислительные задачи, которые не могут быть решены алгоритмами даже за неограниченное время. Например, проблема остановки Тьюринга (данная программа и входные данные, остановится ли программа в конечном итоге при запуске с этим вводом или будет работать вечно). Алан Тьюринг доказал, что не может существовать общего алгоритма решения проблемы остановки для всех возможных пар программа-ввод. Ключевой частью доказательства является то, что машина Тьюринга использовалась как математическое определение компьютера и программы (проблема остановки источника).
Статус NP-полных проблем — еще одна история неудач, NP-полные проблемы — это проблемы, статус которых неизвестен. Алгоритм с полиномиальным временем еще не был обнаружен ни для одной NP-полной задачи, и никто еще не смог доказать, что алгоритма с полиномиальным временем не существует ни для одной из них. Интересно то, что если любую из NP-полных задач можно решить за полиномиальное время, то можно решить и все.

Что такое NP , P , NP-полные и NP-сложные задачи?
P — это набор задач, которые может решить детерминированная машина Тьюринга за полиномиальное время.

NP — это набор проблем принятия решений, которые могут быть решены с помощью N -детерминированной машины Тьюринга за полиномиальное время. P является подмножеством NP (любая задача, которая может быть решена детерминированной машиной за полиномиальное время, также может быть решена недетерминированной машиной за полиномиальное время).
Неформально NP — это набор проблем принятия решений, которые могут быть решены за полиномиальное время с помощью «Алгоритма удачи», волшебного алгоритма, который всегда делает правильный выбор среди заданного набора вариантов (Источник Ref 1).

NP-полные задачи — самые сложные задачи в NP- множестве. Задача решения L является NP-полной, если:
1) L находится в NP (любое заданное решение для NP-полных задач может быть быстро проверено, но эффективного известного решения не существует).
2) Каждая задача из NP сводится к L за полиномиальное время (редукция определена ниже).

Проблема является NP-сложной, если она следует свойству 2, упомянутому выше, и не обязана следовать свойству 1. Следовательно, NP-полный набор также является подмножеством NP-сложного набора.

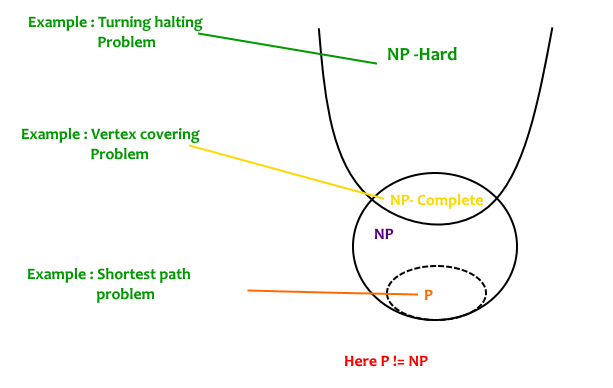
Решение против проблем оптимизации
NP-полнота относится к области проблем принятия решений. Он был создан таким образом, потому что легче сравнивать сложность задач принятия решений, чем задач оптимизации. В действительности, однако, возможность решить задачу решения за полиномиальное время часто позволяет нам решить соответствующую задачу оптимизации за полиномиальное время (используя полиномиальное число вызовов задачи решения). Таким образом, обсуждение сложности проблем принятия решений часто эквивалентно обсуждению сложности задач оптимизации. (Источник Ref 2).
Например, рассмотрим задачу покрытия вершин (данный граф находит набор вершин минимального размера, который покрывает все ребра). Это проблема оптимизации. Соответствующая проблема решения состоит в том, существует ли для неориентированного графа G и k вершинное покрытие размера k?

Что такое редукция?
Пусть L ₁ и L ₂ — две проблемы решения. Предположим, алгоритм A ₂ решает L ₂ . То есть, если y является входом для _L2 , то алгоритм _A2 ответит Да или Нет в зависимости от того, принадлежит ли y _L2 или нет.
Идея состоит в том, чтобы найти преобразование из L ₁ в L ₂ , чтобы алгоритм A ₂ мог быть частью алгоритма A ₁ для решения L ₁ .

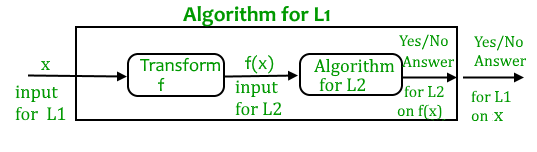
Сокращение обучения, в общем, очень важно. Например, если у нас есть библиотечные функции для решения определенных задач и если мы можем свести новую проблему к одной из решенных, мы сэкономим много времени. Рассмотрим пример задачи, где нам нужно найти путь минимального произведения в заданном ориентированном графе, где произведение пути есть произведение весов ребер вдоль пути. Если у нас есть код для алгоритма Дейкстры для поиска кратчайшего пути, мы можем взять журнал всех весов и использовать алгоритм Дейкстры для поиска минимального пути продукта, а не писать новый код для этой новой задачи.

Как доказать, что данная задача является NP-полной?
Из определения NP-полной не представляется возможным доказать, что задача L является NP-полной. По определению это требует от нас показать, что каждая задача в NP сводится к L за полиномиальное время. К счастью, есть альтернативный способ доказать это. Идея состоит в том, чтобы взять известную NP-полную задачу и свести ее к L. Если полиномиальная редукция возможна, мы можем доказать, что L является NP-полной по транзитивности редукции (если NP-полная задача сводится к L за полиномиальное время, то все задачи сводятся к L за полиномиальное время).

Какая первая задача была доказана как NP-полная?
Должна существовать какая-то первая NP-полная проблема, доказываемая определением NP-полных задач. SAT (проблема булевой выполнимости) — первая NP-полная проблема, доказанная Куком (доказательство см. в книге CLRS).

О NP-полноте всегда полезно знать даже инженерам. Предположим, вас попросили написать эффективный алгоритм решения чрезвычайно важной для вашей компании проблемы. После долгих размышлений вы можете прийти только к экспоненциальному подходу, который непрактичен. Если вы не знаете об NP-полноте, вы можете только сказать, что я не смог придумать эффективный алгоритм. Если вы знаете об NP-полноте и доказываете, что проблема NP-полна, вы можете с гордостью сказать, что полиномиальное решение вряд ли существует. Если возможно решение с полиномиальным временем, то это решение решает большую проблему компьютерных наук, которую многие ученые пытались решить в течение многих лет.

Вскоре мы обсудим другие NP-полные задачи и их доказательство NP-полноты.

Использованная литература:
Видеолекция Массачусетского технологического института о вычислительной сложности
Введение в алгоритмы, 3-е издание Клиффорда Штейна, Томаса Х. Кормена, Чарльза Э. Лейзерсона, Рональда Л. Ривеста.
http://www.ics.uci.edu/~eppstein/161/960312.html

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.