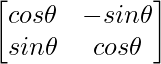Вращение
В реальной жизни мы знаем, что Земля вращается вокруг своей оси, и Луна тоже вращается вокруг своей оси. Но что такое вращение? Кроме того, геометрия имеет дело с четырьмя основными типами преобразований: вращением, отражением, перемещением и изменением размера. В этой статье мы прочитаем о фундаментальной концепции вращения.
Определение вращения
Вращение можно определить как круговое движение объекта вокруг его центра или некоторой оси. Может быть бесконечное количество воображаемых линий или осей, вокруг которых вращается объект. Когда объект вращается, все частицы, составляющие объект, движутся с одинаковой скоростью вокруг этой оси. В общем, вращение — это один из 4-х видов трансформации. Вращательное движение является сложным по сравнению с линейным движением.
Вращение может быть по часовой стрелке или против часовой стрелки, и объект может вращаться под разными углами при вращении. Когда вращение происходит по часовой стрелке, угол поворота считается отрицательным, тогда как в случае вращения против часовой стрелки он считается положительным.
На изображении ниже показан объект, повернутый на разные углы по часовой стрелке и против часовой стрелки.
Давайте посмотрим на формулу вращения.
Формула вращения
Мы знаем, что вращение может осуществляться как по часовой стрелке, так и против часовой стрелки. В математике вращение относится к круговому движению фигуры вокруг фиксированной точки, особенно начала координат. Это приводит к изменению координат точки или фигуры, которые вращаются. Вращение может быть сделано вокруг любого угла. Давайте посмотрим на формулу поворота для некоторых общих углов в обоих направлениях, когда фигура вращается вокруг начала координат.
| Угол и направление вращения | Начальные координаты точки | Координаты точки после поворота |
|---|---|---|
| 90° по часовой стрелке | (х, у) | (у, -х) |
| 90° против часовой стрелки | (х, у) | (-у, х) |
| 180° как по часовой, так и против часовой стрелки | (х, у) | (-х, -у) |
| 270° по часовой стрелке | (х, у) | (-у, х) |
| 270° против часовой стрелки | (х, у) | (у, -х) |
Существует также общая формула вращения, когда вращение происходит не вокруг начала координат, а вокруг точки Q (α, β), которая выглядит следующим образом:
Пусть начальные координаты точки равны (x, y). Тогда координаты точки после поворота (x', y') вокруг точки Q задаются с помощью
(x’, y’) = {α + (x-α)cosθ – (y-β)sinθ, β + (x-α)sinθ – (y-β)cosθ}
Вращательная матрица
С помощью матрицы вращения можно осуществлять вращение в евклидовом пространстве. Матрица поворачивает точку против часовой стрелки на угол θ и предоставляет координаты точки после поворота на этот угол в декартовой плоскости. Матрица вращения R может быть представлена как:
Затем эту матрицу можно умножить на точку, представленную с помощью вектора V, следующим образом:
Вращательная симметрия
Вращательная симметрия — это свойство фигуры, благодаря которому ее форма остается неизменной при вращении по сравнению с исходной формой. Эти фигуры имеют ось симметрии и, как говорят, обладают вращательной симметрией. Вращательную симметрию можно найти многими способами. Самый простой способ — начать вращать объект от 0° до 360°. Если форма объекта при вращении совпадает с его первоначальной формой, то говорят, что он обладает вращательной симметрией при этом угле поворота. Например, квадрат обладает вращательной симметрией при повороте на углы, кратные 90 °, круг обладает вращательной симметрией при всех углах поворота, тогда как треугольник не обладает вращательной симметрией.
Решенные примеры по формуле вращения
Пример 1: Рассчитать координаты точки (5, 3) после поворота на 90° по часовой стрелке.
Решение:
Given, (x, y) = (5, 3)
After rotating the point 90° clockwise the coordinates are given using (y, -x)
Thus, the coordinates of the point after rotation are (3, -5).
Пример 2: Рассчитать координаты точки (3, 4) после поворота на 180° против часовой стрелки.
Решение:
Given, (x, y) = (3, 4)
After rotating the point 180° anti-clockwise the coordinates are given using (-x, -y)
Thus, the coordinates of the point after rotation are (-3, -4).
Пример 3: Координаты точки (x, y) после поворота на 270° по часовой стрелке равны (3, 8). Каковы фактические координаты точки?
Решение:
Given, initial coordinates as (x, y)
Final coordinates after rotation are (3, 8). We know that final coordinates after rotating 270° clockwise are given by (-y, x).
Thus (-y, x) = (3, 8)
So (x, y) = (8, -3)
Thus, the actual coordinates of the point are (8, -3).
Пример 4: Найдите координаты точки (1, -6) после поворота на 90° против часовой стрелки.
Решение:
Given, (x, y) = (1, -6)
After rotating the point 90° clockwise the coordinates are given using (-y, x)
Thus, the coordinates of the point after rotation are (6, 1).
Пример 5: Найдите координаты точки (4, 5), когда она повернута на 45° против часовой стрелки вокруг точки Q(5, 5).
Решение:
Given, (x, y) = (4, 5), θ = 45°(positive because the rotation is anti-clockwise), (α, β) = (5, 5)
Using the rotation formula when the point is rotated about a given point:
(x’, y’) = (α + (x – α) cosθ – (y – β) sinθ, β + (x – α) sinθ – (y – β) cosθ)
= (5 + (4 – 5) cos45° – (5 – 5) sin45°, 5 + (4 – 5) sin45° – (5 – 5) cos45°)
= (5 – 1/√2 – 0, 5 – 1/√2 – 0)
Thus, (x’, y’) = (5 – 1/√2, 5 – 1/√2)
Часто задаваемые вопросы о ротации
Вопрос 1: Что понимается под вращением?
Отвечать:
Rotation is a type of transformation it is defined as the circular motion of an object around a centre or an axis or a fixed point.
Вопрос 2: Напишите о трех типах ротации.
Отвечать:
The three types of rotation are:
- Precession
- Nutation
- Intrinsic Rotation
Вопрос 3: Объясните примеры вращения.
Отвечать:
Some examples of rotation are:
- Motion of Earth along its axis.
- Motion of a Fan.
- Motion of any globe on its axis.
Вопрос 4: Что такое угол поворота?
Отвечать:
Angle of rotation is the amount of rotation measured in degrees.
Вопрос 4: Что такое точка вращения?
Отвечать:
Point of rotation is defined as the point along which a body is rotated.
Связанные ресурсы
- Rotational Kinetic Energy
- Rotational Inertia
- Kinematics of Rotational Motion