Визуализация двумерного распределения Гаусса в R
Распределение Гаусса (более известное как нормальное распределение) является одним из наиболее фундаментальных распределений вероятностей в статистике. Двумерное распределение Гаусса состоит из двух независимых случайных величин. Можно заметить кривую колокола при визуализации двумерного гауссовского распределения. Две случайные величины X 1 и X 2 называются двумерными нормальными, если aX 1 +bX 2 имеет нормальное распределение для всех a, b ∈ R.
Функция распределения вероятностей (PDF) двумерного гауссовского распределения
Функция плотности описывает относительную вероятность случайной величины X в данной выборке. Математически PDF двух переменных X и Y в двумерном распределении Гаусса определяется как:
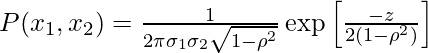
куда,
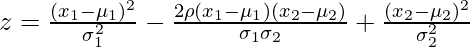
- μ = среднее значение
- σ = стандартное отклонение
- ρ = соотношение x 1 и x 2
Если P = 2, то это двумерное гауссово распределение.
Визуализация двумерного распределения Гаусса в R
Мы будем визуализировать двумерное распределение Гаусса в R, построив их с помощью функций из пакета mnormt() .
install.packages("mnormt")Мы будем использовать dmnorm() для имитации нормального распределения.
dmnorm( ): mnorm(x, mean = rep(0, d), varcov, log = FALSE)
| Параметр | Описание |
|---|---|
| Икс | вектор длины d, где 'd=ncol(varcov)'. |
| иметь в виду | ожидаемое значение распределения. |
| варков | дисперсионно-ковариационная матрица распределения. |
| журнал | если «ИСТИНА» вычисляет логарифм плотности. |
Теперь мы воспользуемся функцией контура() для создания контурного графика, чтобы получить двумерную визуализацию двумерного гауссовского распределения.
R
library(mnormt)set.seed(0)x1 <- seq(-4, 4, 0.1)x2 <- seq(-5, 5, 0.1)mean <- c(0, 0)cov <- matrix(c(2, -1, -1, 2), nrow=2)f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov)y <- outer(x1, x2, f)# create contour plotcontour(x1, x2, y) |
n : sample size. mean : mean of each variable. cov : covariance matrix of the two variables.
Выход:
Для трехмерной визуализации распределения мы создадим поверхностный график, используя функцию пакета persp() .
persp(x = seq(0, 1, length.out = nrow(z)),y = seq(0, 1, length.out = ncol(z)),z, xlim = range(x), ylim = range(y),zlim = range(z, na.rm = TRUE),xlab = NULL, ylab = NULL, zlab = NULL,main = NULL, sub = NULL,theta = 0, phi = 15, r = sqrt(3), d = 1,scale = TRUE, expand = 1,col = “white”, border = NULL, theta = -135, lphi = 0,shade = NA, box = TRUE, axes = TRUE, nticks = 5,ticktype = “simple”, …)
| Параметр | Описание |
|---|---|
| х, у | расположение линий сетки. |
| хлим, йлим, злим | x-, y- и z-пределы. |
| xlab, ylab, zlab | названия осей. |
| тета, фи | углы, определяющие направление взгляда. |
| расширять | коэффициент расширения, применяемый к координатам z. |
| колонка | цвет (цвета) граней поверхности. |
| граница | цвет линии, нарисованной вокруг граней поверхности. |
| оттенок | оттенок на фаске поверхности. |
| коробка | должна отображаться ограничивающая рамка для поверхности. |
| тип тика | виды клещей. |
R
install.packages("mnormt")library(mnormt)set.seed(0)x1 <- seq(-4, 4, 0.1)x2 <- seq(-5, 5, 0.1)mean <- c(0, 0)cov <- matrix(c(2, -1, -1, 2), nrow=2)f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov)y <- outer(x1, x2, f)#create surface plotpersp(x1, x2, y, theta=-20, phi=20, col = "blue", expand=0.8, ticktype="detailed") |
Выход: