Тригонометрические отношения
Тригонометрия — это все о треугольниках или, если быть более точным, о соотношении между углами и сторонами прямоугольного треугольника. У треугольника есть три стороны: гипотенуза, прилежащая и противоположная. Отношение между этими сторонами, основанное на угле между ними, называется тригонометрическим отношением.
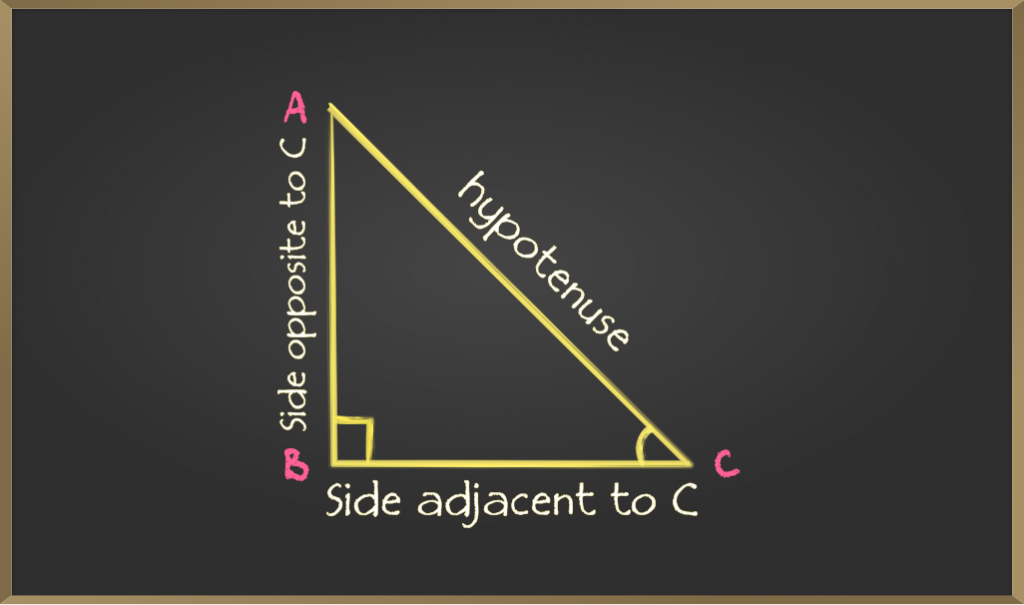
Как показано на рисунке в прямоугольном треугольнике
- Сторона, противолежащая прямому углу, называется гипотенузой
- Сторона, противолежащая углу, называется противолежащей стороной
- У угла С противоположная сторона АВ
- Для угла А противоположная сторона равна ВС
- Сторона, примыкающая к углу, называется прилежащей стороной
- Для угла C смежная сторона равна BC
- Для угла А смежная сторона равна АВ
Что такое тригонометрические отношения?
Существует 6 основных тригонометрических соотношений, составляющих основу тригонометрии. Эти 6 тригонометрических соотношений являются отношениями всех возможных комбинаций в прямоугольном треугольнике.
Эти тригонометрические соотношения называются
- Синус
- Косинус
- Тангенс
- Косеканс
- секанс
- Котангенс
Математический символ θ используется для обозначения угла.
Его (его)
Синус угла определяется отношением длин сторон, противолежащих углу, и гипотенузы. Он представлен как sin θ
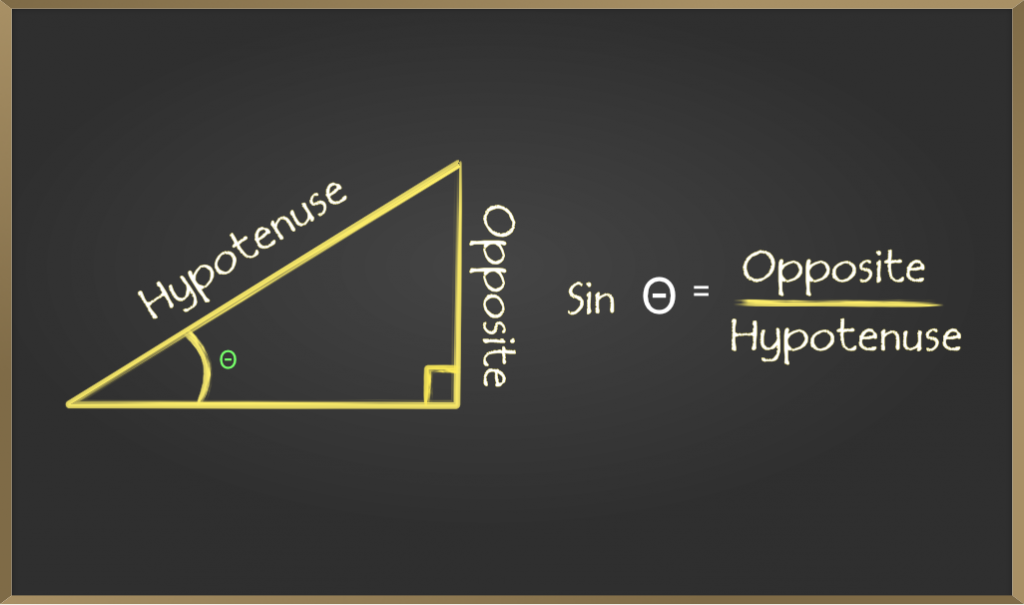
Косинус (cos)
Косинус угла определяется отношением длин сторон, прилежащих к углу, и гипотенузы. Он представлен как cos θ

Тангенс (загар)
Тангенс угла определяется отношением длины стороны, противолежащей углу, и стороны, прилежащей к углу. Он представлен как тангенс θ
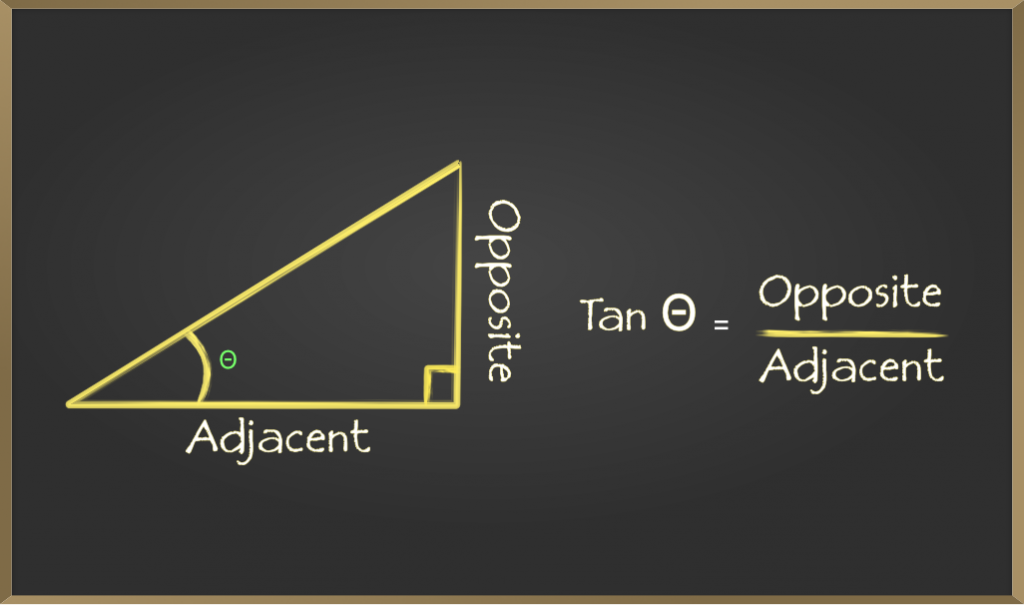
Косеканс (косеканс)
Косеканс угла определяется отношением длины гипотенузы и катета, противолежащего углу. Он представлен как cosec θ
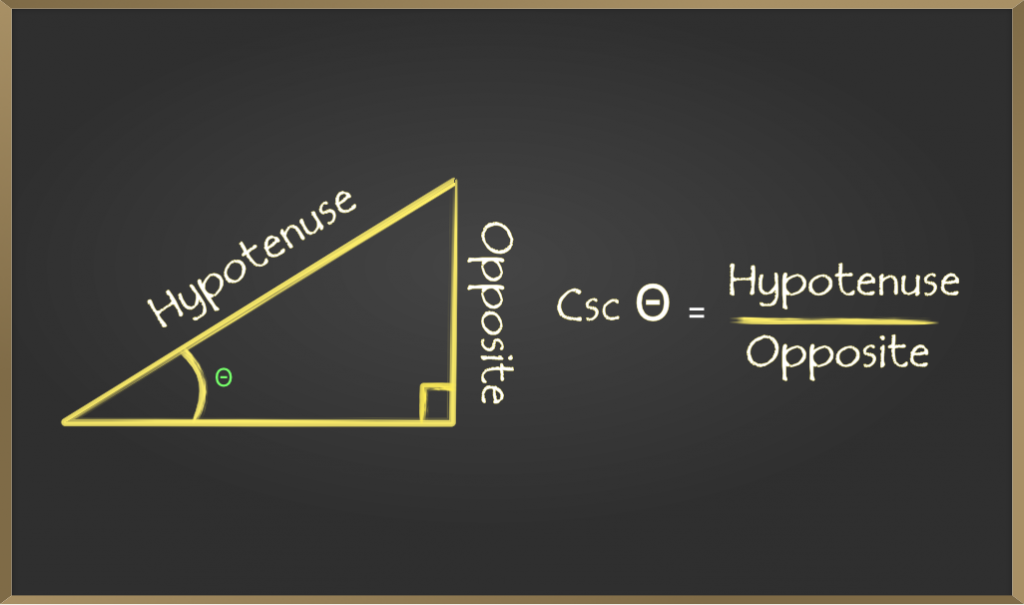
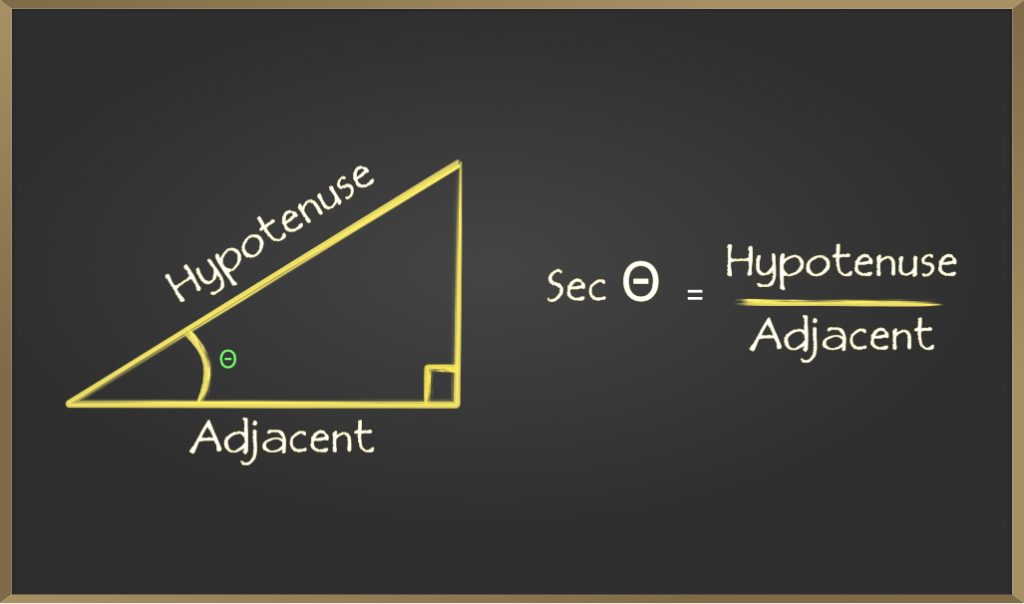
секанс (сек)
Секанс угла определяется отношением длины гипотенузы и катета к прилежащему к углу катету. Он представлен как sec θ
котангенс (колено)
Котангенс угла определяется отношением длины стороны, прилежащей к углу, и стороны, противолежащей углу. Он представлен как кроватка θ.
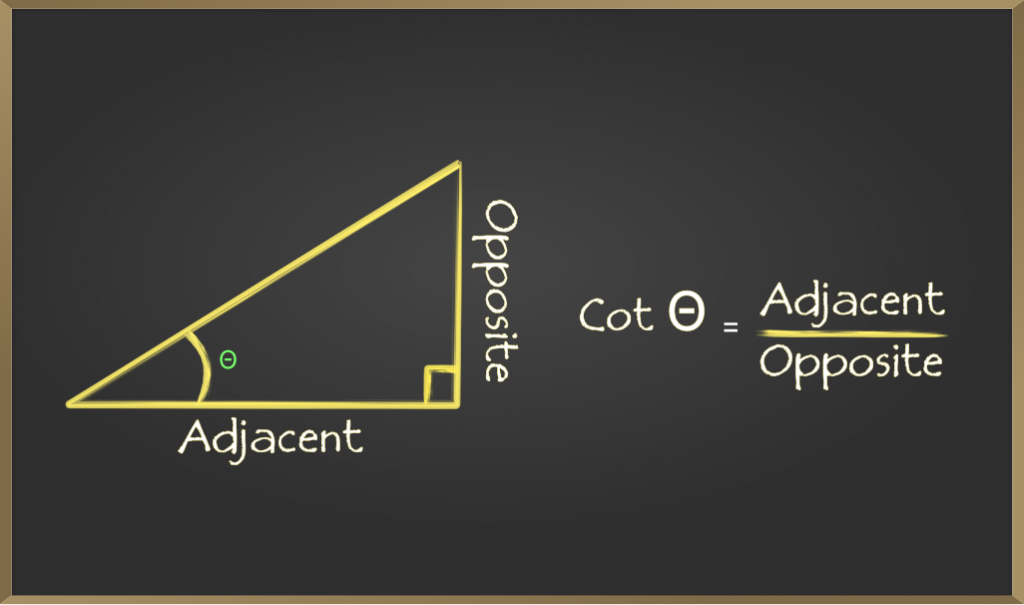
Таблица тригонометрических отношений
Тригонометрические соотношения для любого конкретного угла θ приведены ниже:
Тригонометрическое соотношение | Сокращенное название | Формула |
|---|---|---|
синус | грех | Напротив/гипотенуза |
косинус | потому что | Смежный/гипотенуза |
касательная | загар | Напротив/Смежный |
косеканс | cosec | Гипотенуза/Наоборот |
секущая | сек | Гипотенуза/Смежный |
котангенс | детская кроватка | Смежный/напротив |
Тригонометрическая таблица некоторых конкретных углов
Тригонометрические соотношения для стандартных углов 0°, 30°, 45°, 60° и 90° необходимы для решения тригонометрических соотношений. Различные тригонометрические тождества также необходимы для решения тригонометрических функций. Теперь значения тригонометрических соотношений для конкретных углов, таких как 30 ° , 45 ° и т. д. в таблице ниже:
| Углы | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| загар | 0 | 1/√3 | 1 | √3 | Не определено |
| cosec | Не определено | 2 | √2 | 2/√3 | 1 |
| сек | 1 | 2/√3 | √2 | 2 | Не определено |
| детская кроватка | Не определено | √3 | 1 | 1/√3 | 0 |
Нахождение стороны прямоугольного треугольника с тригонометрическим отношением
Это одно из самых основных и полезных применений тригонометрии с использованием упомянутых тригонометрических соотношений для нахождения длины стороны прямоугольного треугольника, но для этого мы уже должны знать длину двух других сторон или угла и длина одной стороны.
Действия, которые нужно выполнить, если известны одна сторона и один угол:
- Выберите тригонометрическое соотношение, содержащее заданную сторону и неизвестную сторону
- Используйте алгебру, чтобы найти неизвестную сторону
Пример: В прямоугольном треугольнике ABC ∠B = 90° и ∠C = 30°, длина стороны AB равна 4. Найдите длину BC, если тангенс 30° = 1/√3.

Решение:
C = 30°
tan C = tan 30°
= 1/√3
tan C = opposite side/adjacent side
1/√3 = AB/BC
1/√3 = 4/BC
BC = 4√3
Действия, которые необходимо выполнить, если известны две стороны:
- Отметьте известные стороны как смежные, противолежащие или гипотенузу относительно любого из острых углов треугольника.
- Определите, какое тригонометрическое соотношение можно найти по приведенной выше таблице.
- Найдите угол (X)
- Используйте тригонометрическое отношение по отношению к X, которое представляет собой отношение известной стороны к неизвестной стороне.
- Используйте алгебру, чтобы найти неизвестную сторону.
Пример: если две стороны прямоугольного треугольника равны 20 и 10√3, где сторона с длиной 20 является гипотенузой, найдите третью сторону (без использования теоремы Пифагора), учитывая sin 30° = 1/2 и cos 30° = √3/2
Решение:
hypotenuse = 20
adjacent side = 10√3
cos θ = adjacent side / hypotenuse
= 10√3 / 20
θ = √3/2
Решенные примеры на тригонометрические отношения
Пример 1: Найдите значение sin θ, если tan θ = 4/3 и cos θ = 6/10.
Решение:
Given, tan θ = 4/3 and cos θ = 6/10
we know that,
tan θ = sin θ/cos θ
4/3 = sin θ/(6/10)
sin θ = (4/3)×(6/10)
sin θ = 8/10
Пример 2. В прямоугольном треугольнике PQR с прямым углом в точке Q гипотенуза равна PR = 13 см, основание равно QR = 5 см, а перпендикуляр равен PQ = 12 см, и если ∠PQR = θ, то найти sin θ, cos θ и тангенс θ.
Решение:
Given, In ∆PQR,
Hypotenuse, PR = 13 cm
Base, QR = 5 cm
Perpendicular, PQ = 12 cm
now,
sin θ = Perpendicular/Hypotenuse = PQ/PR = 12/13
cos θ = Base/Hypotenuse = QR/PR = 5/13
tan θ = Perpendicular/Base = PQ/QR = 12/5
Пример 3: Найдите значение cos θ, если tan θ = √3 и sin θ = √3/2.
Решение:
Given, tan θ = √3 and sin θ = √3/2
we know that,
tan θ = sin θ/cos θ
√3 = (√3/2)/cos θ
cos θ = (√3/2)/√3
cos θ = 1/2
Пример 4: Найдите значение sec 2 θ, если tan 2 θ = 1
Решение:
Given, tan2 θ = 1…(1)
we know that, sec2 θ – tan2 θ = 1…(2)
By eq (1),
sec2 θ – 1 = 1
sec2 θ = 1 + 1than,
sec2 θ = 2
Часто задаваемые вопросы о тригонометрических соотношениях
Вопрос 1: Каковы различные приложения тригонометрических отношений в реальной жизни?
Отвечать:
Various real life applications of trigonometric ratios are:
- sin and cos functions are used to represent various waves and harmonic functions.
- Trigonometric Ratios are used in the study of architectural engeering, civil engeering, astronomical stuies, etc.
- Trigonometric ratios are used in getting ideaof directions and creating maps.
Вопрос 2: Напишите три основных тригонометрических соотношения.
Отвечать:
The three basic trigonometric ratios are sine (sin), cosine (cos), and tangent (tan)
Вопрос 3: Каковы все шесть тригонометрических отношений?
Отвечать:
All Six 6 trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).
Вопрос 4: Напишите тригонометрические отношения дополнительных углов.
Отвечать:
Two angles whose sum is 90° are called as complementary angles. The formulas for trigonometric ratios of complementary angles are:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- cosec (90°- θ) = sec θ
- sec (90°- θ) = cosec θ
- tan (90°- θ) = cot θ
- cot (90°- θ) = tan θ
Связанные ресурсы
- Trigonometric Identites
- Real-life Application of trigonometry
- Sin and Cos Formulas