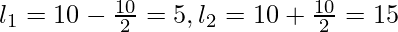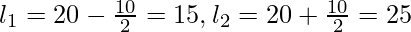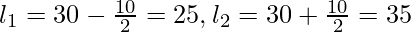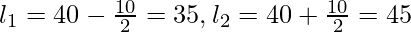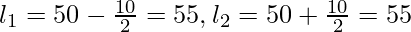Типы частотного распределения

Исследователь не всегда может легко измерить элементы ряда или набора данных. Чтобы сделать данные простыми и легкими для чтения и анализа, элементы ряда помещаются в диапазон значений или пределов. Другими словами, данный необработанный набор данных классифицируется по разным классам с диапазоном, известным как интервалы классов. Каждое изделие данной серии ставится в соответствие с классовым интервалом с помощью счетных столбцов. Количество элементов, встречающихся в определенном диапазоне или интервале класса, отображается в разделе « Частота » по отношению к тому конкретному диапазону класса, к которому принадлежит элемент.

For example,

The marks of a class of 20 students are  11, 27, 18, 14, 28, 18, 2, 22, 11, 24, 22, 11, 8, 20, 25, 28, 30, 12, 11, 8. Prepare a frequency distribution table for the same. 

Solution:

The range of marks of the students is 2- 28. Let us take class intervals 0-5, 5-10, 10-15, 15-20, 20-25, and 25-30. 

 

Типы частотного распределения

Пять различных типов частотного распределения следующие:

1. Эксклюзивная серия

Серия с интервалами классов, в которую включены все элементы, имеющие диапазон от нижнего предела до значения чуть ниже его верхнего предела, известна как эксклюзивная серия. Такой вид частотного распределения известен как эксклюзивный ряд, поскольку частоты, соответствующие интервалу определенного класса, не включают значение его верхнего предела. Например, если интервал классов равен 0-10, а значения данного ряда равны 4, 10, 2, 15, 8 и 9, то только 4, 2, 8 и 9 будут включены в 0-10. интервал 10 занятий. 10 и 15 будут включены в следующий интервал занятий, т.е. 10-20. Кроме того, верхний предел интервала класса является нижним пределом следующего интервала класса.

Example,

Age	Frequency
0-10	5
10-20	2
20-30	8
30-40	1
40-50	4
50-60	6
	Total = 26

From the above table of exclusive series, it can be seen that the upper limits of the first class interval is the lower limit of the second class interval, and so on. Also, as discussed above, if the data includes a value 10, it will be included in the class interval 10-20, not in 0-10. 

2. Инклюзивная серия

Серия с интервалами классов, в которую включены все элементы, имеющие диапазон от нижнего предела до верхнего предела, называется инклюзивной серией. Подобно эксклюзивным рядам, верхняя граница интервала одного класса не повторяется как нижняя граница интервала следующего класса. Следовательно, существует разрыв (от 0,1 до 1) между верхней границей одного класса интервала и нижней границей следующего интервала класса. Например, интервалы классов инклюзивной серии могут быть 0–9, 10–19, 20–29, 30–39 и т. д. В этом случае разрыв между верхней границей интервала одного класса и нижней границей интервала следующего класса равен 1, а интервалы классов не перекрываются друг с другом, как в исключительных сериях.

Иногда бывает сложно выполнить статистический анализ инклюзивных рядов. В этих случаях инклюзивная серия преобразуется в эксклюзивную серию.

Example,

Marks	Frequency
10-19	2
20-29	8
30-39	3
40-49	5
50-59	6
60-69	6
	Total = 30

From the above table of inclusive series, it can be seen that the upper limit of one class interval (say, 9 of interval 0-9) is not the same as the lower limit of the next class interval (10 of interval 10-19). Also, all the values that come under 0-9, including 0 and 9 are included in the frequency against 0-9. 

Преобразование инклюзивной серии в эксклюзивную серию

Для статистического расчета иногда возникает необходимость преобразовать инклюзивный ряд в исключающий ряд. Предположим, в приведенном выше примере некоторые студенты получили такие оценки, как 10,5, 40,5 и т. д. В этом случае эта серия будет преобразована в эксклюзивную серию,

Шаги для преобразования инклюзивной серии в эксклюзивную серию:

• На этом первом шаге рассчитайте разницу между верхней границей класса одного интервала класса и нижней границей следующего интервала класса.
• Следующим шагом является деление разницы на два, а затем добавление полученного значения к верхнему пределу каждого интервала класса и вычитание его из нижнего предела каждого интервала класса.

Example,

The inclusive series of the above example is converted into exclusive series as under.

Marks	Frequency
9.5-19.5	2
19.5-29.5	8
29.5-39.5	3
39.5-49.5	5
49.5-59.5	6
59.5-69.5	6
	Total = 30

Разница между инклюзивной и эксклюзивной сериями

• В инклюзивной серии верхний предел интервала одного класса не совпадает с нижним пределом интервала следующего класса. Существует разрыв в пределах от 0,1 до 1,0 между верхним пределом класса одного интервала класса и нижним пределом класса следующего интервала класса. Однако в Эксклюзивной серии верхний предел интервала одного класса совпадает с нижним пределом интервала следующего класса.
• В случае Inclusive Series значения верхнего и нижнего пределов включаются только в этот интервал класса. Однако в случае Exclusive Series значение верхнего предела интервала класса не включается в этот интервал, вместо этого оно включается в следующий интервал класса.
• Инклюзивная серия подходит для следователя только в том случае, если значение представляет собой полное число, а не десятичную форму. Тем не менее, эксклюзивная серия подходит для исследователя, независимо от того, является ли значение полным числом или десятичной формой.
• Подсчет в Инклюзивной серии возможен только после преобразования ее в Эксклюзивную серию. Однако учет в Exclusive Series возможен во всех случаях.

3. Серия с открытым концом

Иногда нижний предел интервала первого класса и верхний предел класса ряда недоступны; вместо этого в первом случае упоминается Меньше или Ниже (вместо нижнего предела интервала первого класса), а во втором случае упоминается Больше или Выше (вместо верхнего предела интервала последнего класса) . Эти типы серий известны как серии с открытым концом.

Example,

Marks	Frequency
Below 10	4
10-15	2
15-20	6
20-25	3
25-30	8
30 and Above	1

For statistical calculations, if one needs to change the first and last class open-end class interval into limits, it can be done by the general practice of giving the same magnitude or class size to these intervals as the class size of other class intervals. In the above example, the magnitude of other class intervals is 5. Therefore, the open-end class intervals can be written as 5-10 and 30-35, respectively. 

4. Кумулятивный ряд частот

Ряд, частоты которого непрерывно добавляются в соответствии с интервалами класса, известен как кумулятивный ряд частот.

Преобразование простого ряда частот в кумулятивные ряды частот

Простой частотный ряд можно преобразовать в кумулятивный частотный ряд. Есть два способа, которыми это можно сделать. Вот они:

• Выражение кумулятивных частот на основе верхних пределов интервалов классов. Например, выражая 10-20, 20-30 и 30-40 как Меньше 20, Меньше 30 и Меньше 40.
• Выражение кумулятивных частот на основе нижних пределов интервалов классов. Например, выражая 10-20, 20-30 и 30-40 как Больше 20, Больше 30 и Больше 40.

Example,

Convert the following simple frequency series into a cumulative frequency series using both ways. 

Marks	Frequency
0-10	3
10-20	5
20-30	2
30-40	8
40-50	9

Solution:

Method-I (On the Basis of Upper Limits)

Marks	Cumulative Frequency
Less than10	0 + 3 = 3
Less than 20	3 + 5 = 8
Less than 30	8 + 2 = 10
Less than 40	10 + 8 = 18
Less than 50	18 + 9 = 27

Method – II (On the Basis of Lower Limits)

Marks	Cumulative Frequency
More than10	24 + 3= 27
More than 20	19 + 5 = 24
More than 30	17 + 2 = 19
More than 40	9 + 8 = 17
More than 50	0 + 9 = 9

Преобразование кумулятивной частоты в простой частотный ряд

Чтобы получить частоту относительно определенного интервала класса кумулятивного ряда частот, его можно преобразовать в простой ряд частот.

Example,

Determine the frequency of the following cumulative frequency series. 

Marks	Cumulative Frequency (No. of Students)
Less than 10	5
Less than 20	20
Less than 30	35
Less than 40	55
Less than 50	60
Less than 60	75

Solution:

Marks	Cumulative Frequency (No. of Students)	Frequency (No. of Students)
Less than 10	5	5 – 0 = 5
Less than 20	20	20 – 5 = 15
Less than 30	35	35 – 20 = 15
Less than 40	55	55 – 35 = 20
Less than 50	60	60 – 55 = 5
Less than 60	75	75 – 60 = 15

5. Серии частот средних значений

Ряды, в которых вместо интервалов классов даны их средние значения с соответствующими частотами, известны как ряды частот средних значений.

Преобразование частотных рядов среднего значения в простые частотные ряды

Шаги для преобразования частотного ряда среднего значения в простой частотный ряд следующие:

• Первым шагом является определение взаимной разницы между средними значениями.
• Следующим шагом является получение половины полученной разницы.
• Последним шагом преобразования является вычитание результирующей цифры второго шага из среднего значения, чтобы получить нижний предел интервала класса, и добавление результирующей цифры второго шага к среднему значению, чтобы получить верхний предел.

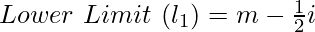
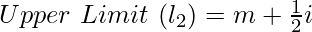
m = среднее значение

i = разница между средними значениями

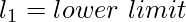
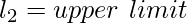
Example,

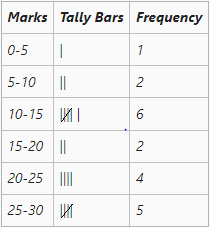
Convert the following Mid-Value Frequency Series into Simple Frequency Series.

Mid-Value	Frequency
10	6
20	3
30	5
40	2
50	8

Solution:

Mid-Value	Frequency	Class Interval
10	6	5-15
20	3	15-25
30	5	25-35
40	2	35-45
50	8	45-55

Calculation:

Difference between mid-values (i) = 10

Mid-Value	Calculation
10
20
30
40
50