Сумма всех уровней в двоичном дереве поиска
Учитывая двоичное дерево поиска, задача состоит в том, чтобы найти горизонтальную сумму узлов, находящихся на одном уровне.
Примеры:
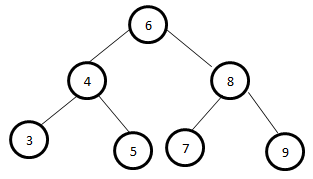
Input:
Output:
6
12
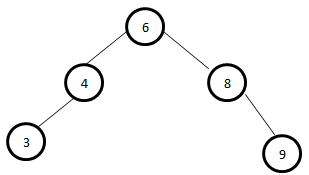
24Input:
Output:
6
12
12
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.
Подход: найдите высоту данного двоичного дерева, тогда количество уровней в дереве будет равно level = height + 1 . Теперь создайте массив sum [] уровней размера, где sum [i] будет хранить сумму всех узлов на i- м уровне. Чтобы обновить этот массив, напишите рекурсивную функцию, которая добавляет данные текущего узла на sum [level], где level - это уровень текущего узла, а затем рекурсивно вызывает тот же метод для дочерних узлов с level как level + 1 .
Below is the implementation of the above approach:
C++
// C++ implementation of the approach#include <iostream>#include <queue>using namespace std; // A Binary Tree Nodestruct Node { int data; struct Node *left, *right;}; // Utility function to create a new tree nodeNode* newNode(int data){ Node* temp = new Node; temp->data = data; temp->left = temp->right = NULL; return temp;} // Utility function to print// the contenets of an arrayvoid printArr(int arr[], int n){ for (int i = 0; i < n; i++) cout << arr[i] << endl;} // Function to return the height// of the binary treeint getHeight(Node* root){ if (root->left == NULL && root->right == NULL) return 0; int left = 0; if (root->left != NULL) left = getHeight(root->left); int right = 0; if (root->right != NULL) right = getHeight(root->right); return (max(left, right) + 1);} // Recursive function to update sum[] array// such that sum[i] stores the sum// of all the elements at ith levelvoid calculateLevelSum(Node* node, int level, int sum[]){ if (node == NULL) return; // Add current node data to the sum // of the current node"s level sum[level] += node->data; // Recursive call for left and right sub-tree calculateLevelSum(node->left, level + 1, sum); calculateLevelSum(node->right, level + 1, sum);} // Driver codeint main(){ // Create the binary tree Node* root = newNode(6); root->left = newNode(4); root->right = newNode(8); root->left->left = newNode(3); root->left->right = newNode(5); root->right->left = newNode(7); root->right->right = newNode(9); // Count of levels in the // given binary tree int levels = getHeight(root) + 1; // To store the sum at every level int sum[levels] = { 0 }; calculateLevelSum(root, 0, sum); // Print the required sums printArr(sum, levels); return 0;} |
Java
// Java implementation of the approach class Sol{ // A Binary Tree Node static class Node { int data; Node left, right; }; // Utility function to create a new tree node static Node newNode(int data) { Node temp = new Node(); temp.data = data; temp.left = temp.right = null; return temp; } // Utility function to print // the contenets of an array static void printArr(int arr[], int n) { for (int i = 0; i < n; i++) System.out.print(arr[i]+ " " ); } // Function to return the height // of the binary tree static int getHeight(Node root) { if (root.left == null && root.right == null) return 0; int left = 0; if (root.left != null) left = getHeight(root.left); int right = 0; if (root.right != null) right = getHeight(root.right); return (Math.max(left, right) + 1); } // Recursive function to update sum[] array // such that sum[i] stores the sum // of all the elements at ith level static void calculateLevelSum(Node node, int level, int sum[]) { if (node == null) return; // Add current node data to the sum // of the current node"s level sum[level] += node.data; // Recursive call for left and right sub-tree calculateLevelSum(node.left, level + 1, sum); calculateLevelSum(node.right, level + 1, sum); } // Driver code public static void main(String args[]){ // Create the binary tree Node root = newNode(6); root.left = newNode(4); root.right = newNode(8); root.left.left = newNode(3); root.left.right = newNode(5); root.right.left = newNode(7); root.right.right = newNode(9); // Count of levels in the // given binary tree int levels = getHeight(root) + 1; // To store the sum at every level int sum[]=new int[levels]; calculateLevelSum(root, 0, sum); // Print the required sums printArr(sum, levels); } } // This code is contributed by andrew1234 |
Python
# Python implementation of above algorithm # Utility class to create a node class Node: def __init__(self, key): self.data = key self.left = self.right = None # Utility function to create a tree nodedef newNode( data): temp = Node(0) temp.data = data temp.left = temp.right = None return temp # Utility function to print# the contenets of an arraydef printArr(arr, n): i = 0 while ( i < n): print( arr[i]) i = i + 1 # Function to return the height# of the binary treedef getHeight(root): if (root.left == None and root.right == None): return 0 left = 0 if (root.left != None): left = getHeight(root.left) right = 0 if (root.right != None): right = getHeight(root.right) return (max(left, right) + 1) sum = [] # Recursive function to update sum[] array# such that sum[i] stores the sum# of all the elements at ith leveldef calculateLevelSum(node, level): global sum if (node == None): return # Add current node data to the sum # of the current node"s level sum[level] += node.data # Recursive call for left and right sub-tree calculateLevelSum(node.left, level + 1) calculateLevelSum(node.right, level + 1) # Driver code # Create the binary treeroot = newNode(6)root.left = newNode(4)root.right = newNode(8)root.left.left = newNode(3)root.left.right = newNode(5)root.right.left = newNode(7)root.right.right = newNode(9) # Count of levels in the# given binary treelevels = getHeight(root) + 1 # To store the sum at every levelsum = [0] * levels calculateLevelSum(root, 0) # Print the required sumsprintArr(sum, levels) # This code is contributed by Arnab Kundu |
C#
// C# implementation of the approach using System; class GFG { // A Binary Tree Node public class Node { public int data; public Node left, right; }; // Utility function to create a new tree node static Node newNode(int data) { Node temp = new Node(); temp.data = data; temp.left = temp.right = null; return temp; } // Utility function to print // the contenets of an array static void printArr(int []arr, int n) { for (int i = 0; i < n; i++) Console.WriteLine(arr[i]); } // Function to return the height // of the binary tree static int getHeight(Node root) { if (root.left == null && root.right == null) return 0; int left = 0; if (root.left != null) left = getHeight(root.left); int right = 0; if (root.right != null) right = getHeight(root.right); return (Math.Max(left, right) + 1); } // Recursive function to update sum[] array // such that sum[i] stores the sum // of all the elements at ith level static void calculateLevelSum(Node node, int level, int []sum) { if (node == null) return; // Add current node data to the sum // of the current node"s level sum[level] += node.data; // Recursive call for left and right sub-tree calculateLevelSum(node.left, level + 1, sum); calculateLevelSum(node.right, level + 1, sum); } // Driver code public static void Main(String []args) { // Create the binary tree Node root = newNode(6); root.left = newNode(4); root.right = newNode(8); root.left.left = newNode(3); root.left.right = newNode(5); root.right.left = newNode(7); root.right.right = newNode(9); // Count of levels in the // given binary tree int levels = getHeight(root) + 1; // To store the sum at every level int []sum = new int[levels]; calculateLevelSum(root, 0, sum); // Print the required sums printArr(sum, levels); } } // This code is contributed by 29AjayKumar |
6 12 24
Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .
Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.