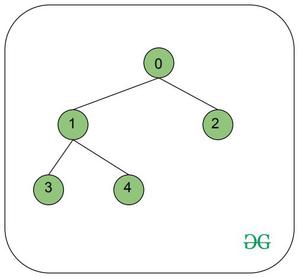
Сумма узлов и соответствующих соседей на пути от корня до вершины V

Опубликовано: 8 Января, 2022

Для корневого дерева с N вершинами, массива values [] , который представляет значение, присвоенное каждому узлу, и вершины V , задача состоит в том, чтобы вычислить сумму значений узлов и ближайших соседей, лежащих на пути от корня ( всегда 0 ) до V.

Примеры:

Input: N = 8, values = {1, 2, 3, 0, 0, 4, 3, 6}, V = 7 
 

Output: 16 
Explanation: 
Path from root (0) to V (7) = 0 -> 1 -> 4 -> 7 
Neighbors of 0 = (2, 3), Sum = 1(node 0) + 3(node 2) + 0(node 3) = 4 
Neighbors of 1 = (5), Sum = 2(node 1) + 4(node 5) = 6 
No neighbor of 4, Sum = 0(node 4) = 0 
No neighbor of 7, Sum = 6(node 7) = 6 
Total sum = 4 + 6 + 0 + 6 = 16

Input: N = 5, values = {5, 6, 2, 9, 0}, V = 2 
 

Output: 13

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход:

Идея состоит в том, чтобы сохранить родительский элемент каждого узла в массиве и добавить значение каждого родителя с его дочерним элементом и сохранить его в родительском узле . Теперь каждый узел будет содержать сумму своего значения и значения соответствующих соседей. Используйте этот массив, чтобы найти необходимую сумму пути от корня до вершины V.

Выполните следующие действия, чтобы решить проблему:

  • Инициализируйте массив для хранения значений каждого узла и его соответствующих соседей с помощью DFS Traversal.
  • Итерируйте от вершины V к корню, используя массив, и продолжайте добавлять значения всех узлов, найденных на пути.
  • Наконец, выведите полученную сумму .

Below is the implementation of the above approach:

C++

// C++ Program to implement
// the above appraoch
#include <bits/stdc++.h>
using namespace std;
 
// Creating Adjacency list
vector<vector<int>> constructTree(int n,
                                  vector<vector<int>> edges)
{
  vector<vector<int>> adjl(n);
 
  for (auto e : edges)
  {
    int u = e[0];
    int v = e[1];
    adjl[u].push_back(v);
    adjl[v].push_back(u);
  }
  return adjl;
}
 
// Function to perform DFS traversal
void DFS(vector<vector<int>> adjl,
         vector<int> &parent, int u, int p)
{
   
  // Initializing parent of each node to p
  parent[u] = p;
 
  // Iterate over the children
  for (int v : adjl[u])
  {
    if (v != p)
    {
      DFS(adjl, parent, v, u);
    }
  }
}
 
// Function to add values of children to
// respective parent nodes
vector<int> valuesFromChildren(vector<int> parent,
                               vector<int> values)
{
  vector<int> valuesChildren(parent.size());
 
  for (int i = 0; i < parent.size(); i++)
  {
     
    // Root node
    if (parent[i] == -1)
      continue;
 
    else
    {
      int p = parent[i];
      valuesChildren[p] += values[i];
    }
  }
  return valuesChildren;
}
 
// Function to return sum of values of
// each node in path from V to the root
int findSumOfValues(int v, vector<int> parent,
                    vector<int> valuesChildren)
{
  int cur_node = v;
  int sum = 0;
 
  // Path from node V to root node
  while (cur_node != -1)
  {
    sum += valuesChildren[cur_node];
    cur_node = parent[cur_node];
  }
 
  return sum;
}
 
// Driver Code
int main()
{
  int n = 8;
 
  // Insert edges into the graph
  vector<vector<int>> edges = {{0, 1}, {0, 2}, {0, 3}, {1, 4},
                               {1, 5}, {4, 7}, {3, 6}};
 
  int v = 7;
 
  // Values assigned to each vertex
  vector<int> values = {1, 2, 3, 0, 0, 4, 3, 6};
 
  // Constructing the tree
  // using adjacency list
  vector<vector<int>> adjl = constructTree(n, edges);
 
  // Parent array
  vector<int> parent(n);
 
  // store values in the parent array
  DFS(adjl, parent, 0, -1);
 
  // Add values of children to the parent
  vector<int> valuesChildren = valuesFromChildren(parent, values);
 
  // Find sum of nodes lying in the path
  int sum = findSumOfValues(v, parent, valuesChildren);
 
  // Add root node since
  // its value is not included yet
  sum += values[0];
  cout << sum << endl;
}
 
// This code is contributed by
// sanjeev2552

Java

// Java Program to implement
// the above appraoch
import java.io.*;
import java.util.*;
 
class GFG {
 
    // Creating Adjacency list
    private static List<List<Integer> >
    constructTree(int n, int[][] edges)
    {
 
        List<List<Integer> > adjl
            = new ArrayList<List<Integer> >();
 
        for (int i = 0; i < n; i++) {
 
            adjl.add(new ArrayList<Integer>());
        }
 
        for (int[] e : edges) {
            int u = e[0];
            int v = e[1];
            adjl.get(u).add(v);
            adjl.get(v).add(u);
        }
 
        return adjl;
    }
 
    // Function to perform DFS traversal
    private static void DFS(
        List<List<Integer> > adjl,
        int[] parent, int u, int p)
    {
 
        // Initializing parent of each node to p
        parent[u] = p;
 
        // Iterate over the children
        for (int v : adjl.get(u)) {
 
            if (v != p) {
 
                DFS(adjl, parent, v, u);
            }
        }
    }
 
    // Function to add values of children to
    // respective parent nodes
    private static int[] valuesFromChildren(
        int[] parent, int[] values)
    {
 
        int[] valuesChildren
            = new int[parent.length];
 
        for (int i = 0; i < parent.length; i++) {
 
            // Root node
            if (parent[i] == -1)
                continue;
 
            else {
                int p = parent[i];
 
                valuesChildren[p] += values[i];
            }
        }
        return valuesChildren;
    }
 
    // Function to return sum of values of
    // each node in path from V to the root
    private static int findSumOfValues(
        int v, int[] parent,
        int[] valuesChildren)
    {
 
        int cur_node = v;
        int sum = 0;
 
        // Path from node V to root node
        while (cur_node != -1) {
 
            sum += valuesChildren[cur_node];
            cur_node = parent[cur_node];
        }
 
        return sum;
    }
 
    // Driver Code
    public static void main(String[] args)
    {
 
        int n = 8;
 
        // Insert edges into the graph
        int[][] edges = { { 0, 1 },
                          { 0, 2 },
                          { 0, 3 },
                          { 1, 4 },
                          { 1, 5 },
                          { 4, 7 },
                          { 3, 6 } };
 
        int v = 7;
 
        // Values assigned to each vertex
        int[] values = new int[] { 1, 2, 3, 0,
                                   0, 4, 3, 6 };
 
        // Constructing the tree
        // using adjacency list
        List<List<Integer> > adjl
            = constructTree(n, edges);
 
        // Parent array
        int[] parent = new int[n];
 
        // store values in the parent array
        DFS(adjl, parent, 0, -1);
 
        // Add values of children to the parent
        int[] valuesChildren
            = valuesFromChildren(parent, values);
 
        // Find sum of nodes lying in the path
        int sum = findSumOfValues(
            v, parent,
            valuesChildren);
 
        // Add root node since
        // its value is not included yet
        sum += values[0];
 
        System.out.println(sum);
    }
}

C#

// C# program to implement
// the above appraoch
using System;
using System.Collections.Generic;
 
class GFG{
 
// Creating Adjacency list
private static List<List<int>> constructTree(int n, int[,] edges)
{
    List<List<int> > adjl = new List<List<int> >();
 
    for(int i = 0; i < n; i++)
    {
         
        adjl.Add(new List<int>());
    }
 
    for(int i = 0; i < edges.GetLength(0); i++)
    {
        int u = edges[i, 0];
        int v = edges[i, 1];
        adjl[u].Add(v);
        adjl[v].Add(u);
    }
 
    return adjl;
}
 
// Function to perform DFS traversal
private static void DFS(List<List<int> > adjl,
                        int[] parent, int u, int p)
{
     
    // Initializing parent of each node to p
    parent[u] = p;
 
    // Iterate over the children
    foreach(int v in adjl[u])
    {
 
        if (v != p)
        {
            DFS(adjl, parent, v, u);
        }
    }
}
 
// Function to add values of children to
// respective parent nodes
private static int[] valuesFromChildren(int[] parent,
                                        int[] values)
{
 
    int[] valuesChildren = new int[parent.Length];
 
    for(int i = 0; i < parent.Length; i++)
    {
         
        // Root node
        if (parent[i] == -1)
            continue;
 
        else
        {
            int p = parent[i];
            valuesChildren[p] += values[i];
        }
    }
    return valuesChildren;
}
 
// Function to return sum of values of
// each node in path from V to the root
private static int findSumOfValues(int v, int[] parent,
                                   int[] valuesChildren)
{
 
    int cur_node = v;
    int sum = 0;
 
    // Path from node V to root node
    while (cur_node != -1)
    {
         
        sum += valuesChildren[cur_node];
        cur_node = parent[cur_node];
    }
    return sum;
}
 
// Driver Code
public static void Main(string[] args)
{
    int n = 8;
 
    // Insert edges into the graph
    int[, ] edges = { { 0, 1 }, { 0, 2 }, { 0, 3 },
                      { 1, 4 }, { 1, 5 }, { 4, 7 },
                      { 3, 6 } };
 
    int v = 7;
 
    // Values assigned to each vertex
    int[] values = new int[] { 1, 2, 3, 0,
                               0, 4, 3, 6 };
 
    // Constructing the tree
    // using adjacency list
    List<List<int>> adjl = constructTree(n, edges);
 
    // Parent array
    int[] parent = new int[n];
 
    // store values in the parent array
    DFS(adjl, parent, 0, -1);
 
    // Add values of children to the parent
    int[] valuesChildren = valuesFromChildren(parent,
                                              values);
 
    // Find sum of nodes lying in the path
    int sum = findSumOfValues(v, parent,
                              valuesChildren);
 
    // Add root node since
    // its value is not included yet
    sum += values[0];
 
    Console.WriteLine(sum);
Структуры данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Различия между структурой данных массива и словаря
21 Января, 2023
TCS SDE Sheet: Вопросы и ответы для интервью
12 Января, 2023
Множественные сравнения в очереди приоритетов С++?
6 Января, 2023
Когда использовать Queue over ArrayList в Java?
6 Января, 2023
Введение в связанный список — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Введение в массивы — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Как подготовиться к ICFP или Международной конференции по функциональному программированию?
12 Декабря, 2022