Собственные значения и собственные векторы в MATLAB

Собственные значения и собственные векторы являются свойствами квадратной матрицы.

Позволять 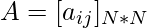— матрица N*N , X — вектор размера N*1 и 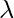быть скаляром .

Тогда значения X, 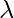удовлетворяющее уравнению 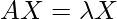являются собственными векторами и собственными значениями матрицы A соответственно.

• Матрица размера N*N имеет N собственных значений
• Каждому собственному значению соответствует собственный вектор.

Matlab позволяет пользователям находить собственные значения и собственные векторы матрицы, используя метод eig() . Различный синтаксис метода eig() :

• е = еиг(А)
• [V,D] = eig(A)
• [V,D,W] = eig(A)
• е = eig(A,B)

Давайте подробно обсудим приведенные выше синтаксисы:

е = еиг(А)

• Он возвращает вектор собственных значений квадратной матрицы A .

Выход :

[V,D] = eig(A)

• Он возвращает диагональную матрицу D , имеющую диагонали в качестве собственных значений.
• Он также возвращает матрицу правильных векторов как V .
• Нормальные собственные векторы называются правыми собственными векторами .
• V представляет собой набор N собственных векторов каждого размера N * 1 (A - размер N * N), который удовлетворяет A * V = V * D

Выход :

[V,D,W] = eig(A)

• Наряду с диагональной матрицей собственных значений D и правых собственных векторов V он также возвращает левые собственные векторы матрицы A.
• Левый собственный вектор u — это матрица размера 1*N , которая удовлетворяет уравнению u*A = k*u , где k — левое собственное значение матрицы A .
• W — это набор N левых собственных векторов матрицы A, удовлетворяющих условию W'*A = D*W' .

Выход :

е = eig(A,B)

• Он возвращает обобщенные собственные значения двух квадратных матриц A и B одинакового размера.
• Обобщенное собственное значение λ и соответствующий собственный вектор v удовлетворяют условиям Av=λBv .

Выход :