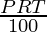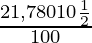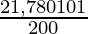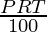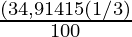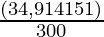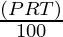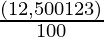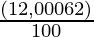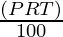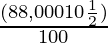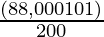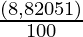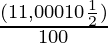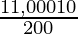Решения NCERT класса 8 - Глава 8 Сравнение количеств - Упражнение 8.3

Вопрос 1. Рассчитайте сумму и сложные проценты на

(i) 10 800 рупий за 3 года по ставке 12 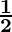% годовых, начисляемых ежегодно.

(ii) 18 000 рупий на двоих 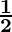лет под 10% годовых, начисленных ежегодно.

(iii) 62 500 рупий за 1 человека 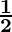лет под 8% годовых с начислением раз в полгода.

(iv) 8000 рупий на 1 год под 9% годовых с начислением сложных процентов каждые полгода.

(v) 10 000 рупий на 1 год под 8% годовых с начислением сложных процентов каждые полгода.

Решение:

(i) Given values are,

P = Rs 10,800

R = 12  % per annum =  %

T = 3 Years

As it is compounded annually then, n = 3 times.

We have,

A = P (1 + )ⁿ

A = 10,800 (1+ )³ 

A = 10,800 (1+ )³

A = 10,800 ()³

A = Rs 15,377.34

CI = A – P

CI = 15,377.34 – 10,800

CI = Rs 4,577.34

Hence, the amount = Rs 15,377.34 and 

Compound interest = Rs 4,577.34

(ii) Given values are,

P = Rs 18,000

R = 10 % per annum 

T = 2 Years

As it is compounded annually then, n = 2 times.

We have,

A = P (1 + )ⁿ

A = 18,000 (1+ )^2½

What we will do here is Firstly we know 2 Years is 2 years and 6 months which can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.

The amount for 2 years has to be calculated : 

A = 18,000 (1+ )²

A = 18,000 ()²

A = Rs 21,780

CI = A – P

CI = 21,780 – 18,000

CI = Rs 3,780

Now, The amount for  year has to be calculated: 

New P is equal to the amount after 2 Years. Hence, 

P = Rs 21,780

R = 10 % per annum 

T =  year

SI = 

SI = 

SI = 

SI = Rs 1,089

Hence, the Total amount = A + SI

                                           = 21,780 + 1,809

                                           = Rs 22,869  

Total compound interest = CI + SI

                                          = 3,780 + 1,809

                                          = Rs 4,869   

(iii) Given values are,

P = Rs 62,500

R = 8 % per annum hence 4% Half Yearly

T = 1 Years

As it is compounded Half yearly then, n = 3 times. (1 Years contains 3 half years)

We have,

A = P (1 + )ⁿ

A = 62,500 (1+ )³

A = 62,500 (1+ )³

A = 62,500 ()³

A = Rs 70,304

CI = A – P

CI = 70,304 – 62,500

CI = Rs 7,804

Hence, the amount = Rs 70,304 and

Compound interest = Rs 7,804

(iv) Given values are,

P = Rs 8,000

R = 9 % per annum hence,  % Half Yearly

T = 1 Year

As it is compounded Half yearly then, n = 2 times. (1 Year contains 2 half years)

We have,

A = P (1 + )ⁿ

A = 8,000 (1+ )²

A = 8,000 (1+ )²

A = 8,000 ()²

A = Rs 8,736.20

CI = A – P

CI = 8,736.20 – 8,000

CI = Rs 736.20

Hence, the amount = Rs 8,736.20 and

Compound interest = Rs 736.20

(v) Given values are,

P = Rs 10,000

R = 8 % per annum  hence, 4% Half Yearly

T = 1 Year

As it is compounded Half yearly then, n = 2 times. (1 Year contains 2 half years)

We have,

A = P (1+  )ⁿ

A = 10,000 (1+ ())²

A =10,000 (1+ ())²

A = 10,000 ()²

A = Rs 10,816

CI = A – P

CI = 10,816- 10,000

CI = Rs 816

Hence, the amount = Rs 10,816 and

Compound interest = Rs 816

Вопрос 2. Камала заняла 26 400 рупий в банке, чтобы купить скутер, со ставкой 15% годовых, начисленной ежегодно. Какую сумму она заплатит по истечении 2 лет и 4 месяцев, чтобы погасить ссуду?

Решение:

Here, Given values are,

P = Rs 26,400

R = 15 % per annum 

T = 2 Years and 4 months, which is 2  years

As it is compounded annually then, n = 2 times

We have,

A = P (1 + )ⁿ

A = 26,400 (1 + ()^2(1/3)

What we will do here is Firstly 2 years and 4 months which can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.

The amount for 2 years has to be calculated:

A = 26,400 (1+ ()²

A = 26,400 (1+ ()²

 A = 26,400 ()²

A = Rs 34,914

Now, The amount for (1/3) year (4 months) has to be calculated :

New P is equal to the amount after 2 Years. Hence,

P = Rs 34,914

R = 15 % per annum 

T =  year

SI = 

SI = 

SI = 

SI = 1,745.70

Hence, the Total amount = A + SI

                                       = 34,914 + 1,745.70

                                       = Rs 36,659.70

Hence, the amount to be paid by Kamla = ₹ 36,659.70

Вопрос 3. Фабина берет 12 500 рупий под 12% годовых на 3 года под простые проценты, а Радха заимствует такую же сумму на тот же период под 10% годовых, начисленных ежегодно. Кто платит больше процентов и на сколько?

Решение:

Let’s see each case 

Fabina Case: at simple interest

P = 12,500

R = 12% per annum  

T = 3 Years

SI = 

SI = 

SI = Rs 4,500

Radha Case: at compound interest

P = 12,500

R = 10% per annum  

T = 3 Years

As it is compounded annually then, n = 3 times

We have,

A = P (1 + )ⁿ

A = 12,500 (1 + ())³

A =12,500 (1 + )³

A = 12,500 ()³

A = Rs 16,637.5

CI = A – P

CI = 16,637.5 – 12,500

CI = 4,137.5

Clearly we can see that Fabina paid more interest, and she paid

4,500 – 4,137.5 = Rs 362.5 more than Radha

Вопрос 4. Я взял в долг 12 000 рупий у Джамшеда под простую процентную ставку 6% годовых сроком на 2 года. Если бы я взял эту сумму в долг под 6% годовых, какую дополнительную сумму мне пришлось бы заплатить?

Решение:

Lets see each case First

At simple interest

P = 12,000

R = 6% per annum  

T = 2 Years

SI = 

SI = 

SI = Rs 1,440

At compound interest

P = 12,000

R = 6% per annum  

T = 2 Years

As it is compounded annually then, n = 2 times

We have,

A = P (1 + )ⁿ

A = 12,000 (1+ ())²

A =12,000 (1+ ())²

A = 12,000 ()²

A = Rs 13,483.2 

CI = A – P

CI = 13,483.2 – 12,000

CI = 1,483.2

Clearly we can see that,

1,483.2 – 1,440 = Rs 43.2

Hence, the extra amount to be paid = ₹ 43.20

Вопрос 5. Васудеван инвестировал 60 000 рупий под 12% годовых, начисляемых раз в полгода. Какую сумму он получит

(а) через 6 месяцев?

(б) через 1 год?

Решение:

Let’s see each case 

(a) 

P = 60,000

R = 12% per annum (6% Half yearly)

T = 6 Months

As it is compounded Half Yearly then, n = 1 times (as 6 months is 1 half year)

We have,

A = P (1 + )ⁿ

A =60,000 (1+ ())¹

A =60,000 (1+ ())¹

A = 60,000 ()¹

A = Rs 63,600

He would get Rs 63,600 after 6 Months.

(b)

P = 60,000

R = 12% per annum (6% Half yearly)

T = 1 Year

As it is compounded Half Yearly then, n = 2 times (as 1 Year is 2 half year)

We have,

A = P (1 + )ⁿ

A = 60,000 (1+ ())²

A = 60,000 (1+ ())²

A = 60000 ()²

A = Rs 67,416

He would get Rs 67,416 after 1 Year.

Вопрос 6. Ариф взял в банке ссуду в размере 80 000 рупий. Если процентная ставка составляет 10% годовых, найдите разницу в суммах, которые он будет платить через 1 год. лет, если интерес

(а) ежегодно.

(б) начисляются раз в полгода.

Решение:

Let’s see each case 

(a) Compounded Annually

P = 80,000

R = 10% per annum

T = 1 Year

As it is compounded annually then, n = 1  times

We have,

A = P (1 + )ⁿ

A = 80,000 (1 + ()^1½

What we will do here is Firstly we know 1 Years is 1 year and 6 months which can be calculated by first calculating the amount to 1 year using CI formula and then calculating the simple interest by using SI formula.

The amount for 1 years has to be calculated :

A = 80,000 (1+ ())¹

A = 80,000 (1+ ()¹

A = 80,000 ()¹

A = Rs 88,000

Now, The amount for  Year (6 months) has to be calculated :

New P is equal to the amount after 1 Year. Hence,

P = Rs 88,000

R = 10 % per annum

T = Year

SI = 

SI = 

SI = 

SI = 4,400

Hence, the Total amount = A + SI

                                        = 88,000 + 4,400

                                        = Rs 92,400

(b) Compounded Half-yearly

P = 80,000

R = 10% per annum (5 % Half Yearly)

T = 1 Year

As it is compounded annually then, n = 3 times (as 1 Year is 3 half year)

We have,

A = P (1 + )ⁿ

A = 80,000 (1+ ()³

A = 80,000 (1+ ()³

A = 80,000 ()³

A = Rs 92,610

Hence, the Total amount = Rs 92,610

Вопрос 7. Мария инвестировала 8 000 рупий в бизнес. Ей будут выплачиваться проценты в размере 5% годовых, начисляемые ежегодно. Находить

(а) Сумма, начисленная на ее имя в конце второго года.

(b) Проценты за 3-й год.

Решение:

Let’s see each case 

Here, 

P = 8,000

R = 5% Per annum

(a) The amount credited against Maria’s name at the end of the second year.

T = 2 Year

As it is compounded annually then, n = 2 times

We have,

A = P (1 + )ⁿ

A = 8,000 (1+ ())²

A = 8,000 (1+ ())²

A = 8,000 ()²

A = Rs 8,820

Hence, the amount credited against Maria’s name at the end of the second year = Rs 8,820

(b) The interest for the 3rd year.

T = 3 Year

As it is compounded annually then, n = 3 times

We have,

A = P (1+ )ⁿ

A = 8,000 (1+ ())³

A = 8,000 (1+ ())³

A = 8,000 ()³

A = Rs 9,261

The interest for the 3rd year = Amount after 3 years – Amount after 2 Years

                                                 = 9,261 – 8,820

                                                 = Rs 441

Another Solution for (b)

As we can calculate interest of 3^rd year by having 2^nd Year Amount as P.

P = 8,820

R = 5% per annum

T = 1 Year (2^nd to 3^rd year)

SI = 

SI = 

SI = Rs 441

The interest for the 3rd year = Rs 441

Вопрос 8. Найдите сумму и сложные проценты на 10 000 рупий за 1 лет под 10% годовых, начисляются каждые полгода. Будет ли этот процент больше, чем тот, который он получил бы, если бы он начислялся ежегодно?

Решение:

Let’s see each cases

Compounded Annually

P = 10,000

R = 10% per annum

T = 1 Year

As it is compounded annually then, n = 1  times

We have,

A = P (1 + )ⁿ

A = 10,000 (1 + ()^1½

What we will do here is Firstly we know 1½ Years is 1 year and 6 months which can be calculated by first calculating the amount to 1 year using CI formula and then calculating the simple interest by using SI formula.

The amount for 1 year has to be calculated:

A = 10,000 (1 + )¹

A = 10,000 (1+ )¹

A = 10,000 ()¹

A = Rs 11,000

CI = A – P

CI = 11,000-10,000

CI = 1,000

Now, The amount for  Year (6 months) has to be calculated :

New P is equal to the amount after 1 Year. Hence,

P = Rs 11,000

R = 10 % per annum

T = Year

SI = 

SI = 

SI = 

SI = 550

Hence, the Total Interest (compounded annually)= CI + SI

                                       = 1,000 + 550

                                       = Rs 1,550

Compounded Half-yearly

P = 10,000

R = 10% per annum (5 % Half Yearly)

T = 1 Year

As it is compounded annually then, n = 3 times (as 1 Year is 3 half year)

We have,

A = P (1 + )ⁿ

A = 10,000 (1 + ()³

A = 10,000 (1+ )³

A = 10,000 ()³

A = Rs 11,576.25

CI = A – P

CI = 11,576.25 – 10,000

CI = 1,576.25

Hence, the Total Interest (compounded Half Yearly) = Rs 11576.25

Difference between the two interests = 1,576.25 – 1,550 = Rs 26.25

Hence, the interest will be Rs 26.25 more when compounded half-yearly than the interest when compounded annually.

Вопрос 9. Найдите сумму, которую Рам получит по 4096 рупий, если он отдал ее на 18 месяцев по 12. % годовых, проценты начисляются раз в полгода .

Решение:

Let’s see this case

P = Rs 4,096

R = 12  % per annum ( % Half yearly)

T = 18 Months = 1 Year

As it is compounded Half yearly then, n = 3 Times

We have,

A = P (1 + )ⁿ

A = 4,096 (1+ ()³

A = 4,096 (1+ )³

A = 4,096 (1+ ()³

A = 4,096 ()³

A = Rs 4,913

Ram will get the amount = Rs 4,913

Вопрос 10. Население населенного пункта увеличилось до 54 000 в 2003 году со скоростью 5% в год.

(а) найти численность населения в 2001 году.

(б) каково было бы его население в 2005 г.?

Решение:

Here,

P = 54,000 (in 2003)

R = 5% per annum

(a) Population in 2001

T = 2 Years (back)

n = 2

Population in 2003 = Population in 2001 (1 + )ⁿ

54,000 = P₁ (1+())²

54,000 = P1 ()²

54,000 = P1 ()

P1 = 54,000 ()

P1 = 48,979.59

P1 = 48,980 (approx.).

Population in 2001 was 48,980 (approx.).

(b) Population in 2005

T = 2 Years

n = 2

We have,

A = P (1 + )ⁿ

A = 54,000 (1+ )²

A = 54,000 (1+ ()²

A = 54,000 ()²

A = 59,535

Population in 2005 will be 59,535

Вопрос 11. В лаборатории количество бактерий в одном эксперименте увеличивалось со скоростью 2,5% в час. Найдите бактерии через 2 часа, если изначально было 5,06 000.

Решение:

Here,

P = 5,06,000

R = 2.5% per hour

T = 2 hours

We have,

A = P (1 + )ⁿ

A = 5,06,000 (1+ )²

A = 5,06,000 (1+ )²

A = 5,06,000 (1+ )²

A = 5,06,000 ()²

A = 5,31,616.25

A = 5,31,616 (approx.)

Bacteria at the end of 2 hours = 5,31,616 (approx.)

Вопрос 12. Самокат был куплен за 42 000 рупий. Его стоимость обесценивалась из расчета 8% годовых. Найдите его стоимость через год.

Решение:

Here,

P = 42,000

R = 8% per annum (depreciated)

T = 1 Year

We have,

A = P (1 + )ⁿ

A = 42,000 (1- )¹ (negative sign because the price is reduced)

A = 42,000 (1- ()¹

A = 42,000 ()¹

A = Rs 38,640

The value of scooter after one year will be = Rs 38,640