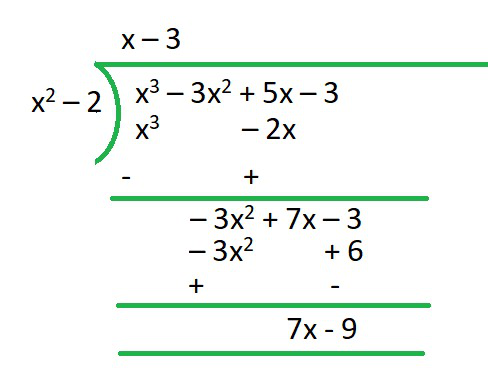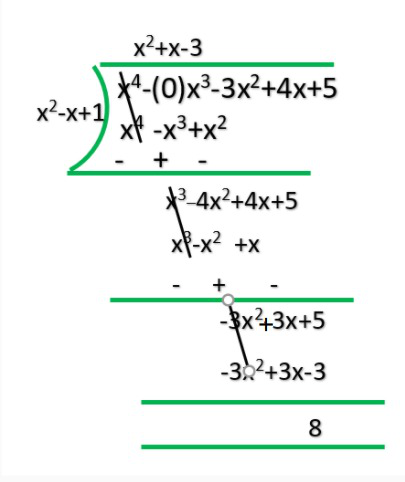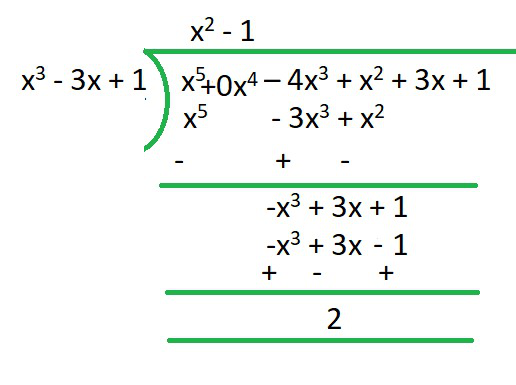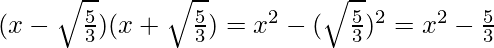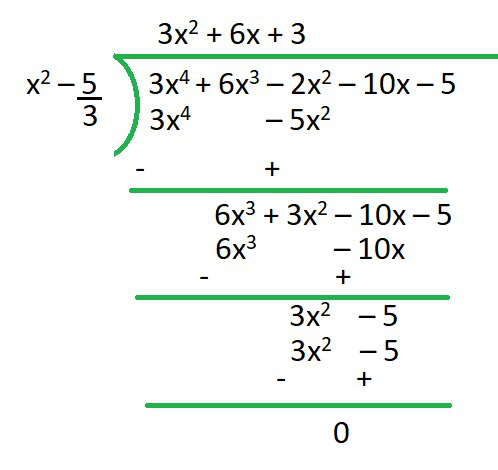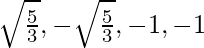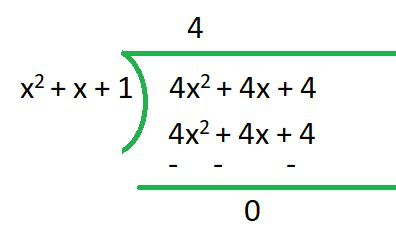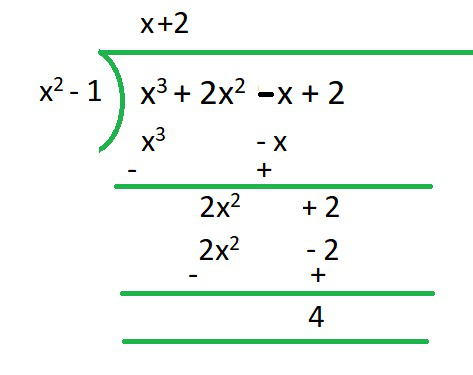Решения NCERT класса 10 - Глава 2, Полиномы - Упражнение 2.3

Вопрос 1. Разделите многочлен p (x) на многочлен g (x) и найдите частное и остаток в каждом из следующих утверждений:

(i) p (x) = x ³ - 3x ² + 5x - 3, g (x) = x ² - 2

(ii) p (x) = x ⁴ - 3x ² + 4x + 5, g (x) = x ² + 1 - x

(iii) p (x) = x ⁴ - 5x + 6, g (x) = 2 - x ²

Решение:

i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2

R = 7x-9

Q = x-3

ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x

R = 8

Q = x²+x-3

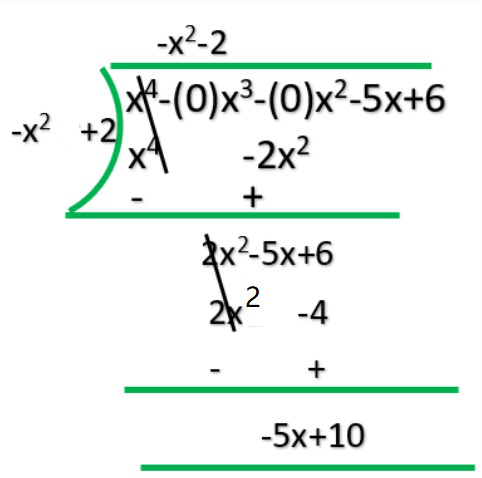
iii) p(x) = x⁴– 5x + 6, g(x) = 2 – x²

Q = -x²-2

R = -5x+10

Вопрос 2. Проверьте, является ли первый многочлен множителем второго многочлена, разделив второй многочлен на первый многочлен.

(я) т ² - 3, ⁴ 2t + 3t ³ - 2t ² - ет - 12

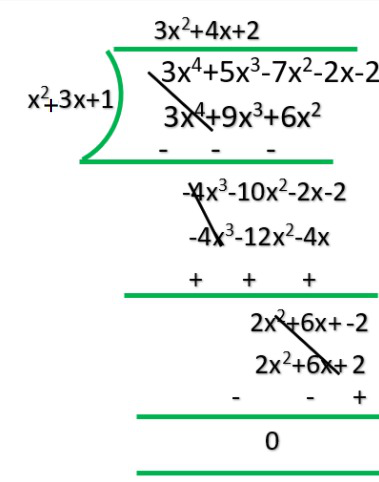
(II) х ² + 3х + 1, 3x ⁴ + 5х ³ - 7x ² + 2x + 2

(iii) x ³ - 3x + 1, x ⁵ - 4x ³ + x ² + 3x + 1

Решение:

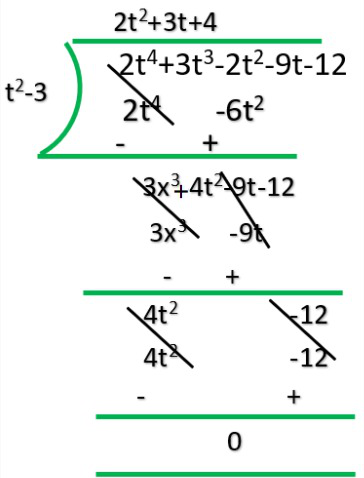
i) t² – 3, 2t⁴ + 3t³ – 2t²– 9t – 12

Q = 2t³+3t+4

R = 0

Yes 1^st polynomial is factor of 2^nd polynomial. 

ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2

R = 0

Q = 3x²-4x+2

iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

R = x²-1

Q = 2

Вопрос 3. Получите все остальные нули 3x ⁴ + 6x ³ - 2x ² - 10x - 5, если два из его нулей равны √ (5/3) и -√ (5/3).

Решение:

R = 0

Q = 3x²+6x+3

∴ we are factorizing

3x²+6x+3

x²+2x+1

(x+1)²

(x+1)  (x+1) = 0

∴ x = -1 and x = -1

Вопрос 4. При делении x ³ - 3x ² + x + 2 на многочлен g (x) частное и остаток составили x - 2 и -2x + 4 соответственно. Найдите g (x).

Решение:

Dividend = Divisor * Quotient + Remainder

x³-3x²+3x-2/x-2

R = 0

Q = x² -x +1

Answer: g(x)=x²-x+1

Вопрос 5. Приведите примеры многочленов p (x), g (x), q (x) и r (x), которые удовлетворяют алгоритму деления и:

(i) deg p (x) = deg q (x)

(ii) deg q (x) = deg r (x)

(iii) deg r (x) = 0

Решение:

i) deg p(x) = deg q(x)

p(x)=2x²-2x+14, g(x)=2

p(x)/g(x)=2x²-2x+14/2=(x²-x+7)

=x²-x+7=q(x)

=q(x)=x²-x+7

r(x)=0

ii) deg q(x)=deg r(x)

p(x)=4x²+4x+4, g(x)=x²+x+1

q(x) = 4

r(x) = 0

∴Here deg q(x)=deg r(x)

iii) deg r(x)=0

p(x)=x³+2x²-x+2 ,g(x)=x²-1

q(x) = x+2

r(x) = 4

deg of r(x) = 0