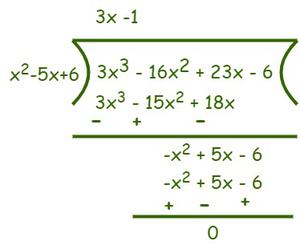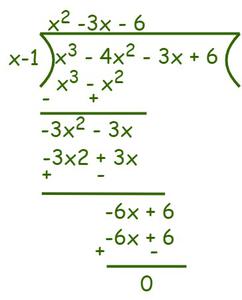Решение кубических уравнений – методы и примеры
В математике полиномом называется алгебраическое выражение, состоящее из переменных, коэффициентов и арифметических операций, таких как сложение, вычитание, умножение или деление. Общая форма многочлена: ax n + bx n-1 + cx n-2 +… + 1. Уравнение — это математическое выражение, выражающее отношение между двумя значениями. Алгебраическое уравнение — это уравнение в форме ax n + bx n-1 + cx n-2 +… + 1 = 0. Например, 2x-5 = 0 является примером алгебраического уравнения, где (2x- 5) является многочленом. Существуют различные типы алгебраических уравнений в зависимости от высшей степени переменной, такие как линейное уравнение, квадратное уравнение, кубическое уравнение и т. д.
Кубическое уравнение — это алгебраическое уравнение, в котором наивысшая степень многочлена равна 3. Некоторые примеры кубических уравнений:
х 3 – 4 х 2 + 15 х – 9 = 0, 2 х 3 – 4 х 2 + 5 = 0 и т.д.
Общая форма кубического уравнения:
ax3 + bx2 + cx + d = 0, a ≠ 0
where,
a, b, and c are the coefficients and d is the constant.
Как решать кубические уравнения?
Кубическое уравнение можно решить традиционным способом, сведя его к квадратному уравнению, а затем решив либо с помощью факторизации, либо с помощью квадратной формулы. Подобно тому, как квадратное уравнение имеет два корня, кубическое уравнение имеет три корня. Кубическое уравнение может иметь три действительных корня или действительный корень и два мнимых корня. Любое уравнение, в том числе и кубическое, всегда должно сначала приводиться в стандартной форме.
Например, если задано уравнение 2x 2 -5 = x + 4/x, то мы должны привести его к стандартной форме, т. е. 2x 3 -x 2 -5x-4 = 0. Теперь мы можем решить уравнение любым подходящим методом.
Кубическое уравнение можно решить следующими способами:
- Поиск целочисленных решений с помощью списков факторов
- Использование графического метода
Решение кубического уравнения с использованием множителей многочлена
Пример: Найдите корни уравнения f(x) = 3x 3 −16x 2 + 23x − 6 = 0.
Решение:
Given expression: f(x) = 3x3 −16x2 + 23x − 6 = 0.
First, factorize the polynomial to get roots.
Since the constant is +6 the possible factors are 1, 2, 3, 6.
f(1) = 3 – 16 + 23 – 6 ≠ 0
f(2) = 24 – 64 + 46 – 6 = 0
f(3) = 81 – 144 + 69 – 6 = 0
f(6) = 648 – 576 + 138 – 6 ≠ 0
We know that, if f(a) = 0, then (x-a) is a factor of f(x).
So, (x – 2) and (x – 3) are factors of f(x). Now to find the remaining factors use the synthetic division method.
(x – 2)(x – 3) = (x2 – 5x + 6)
So, (3x- 1) is another factor of f(x).
So,
the roots of the given equation are 1/3, 2, and 3.
Решение уравнения графическим методом
Кубическое уравнение решается графически, когда вы не можете решить данное уравнение, используя другие методы. Итак, нам нужен точный рисунок данного кубического уравнения. Корни уравнения — это точки, в которых график пересекает ось X. Число действительных решений кубического уравнения равно количеству пересечений графика кубического уравнения с осью x.
Пример: Найдите корни уравнения f(x) = x 3 - 4x 2 - 9x + 36 = 0, используя графический метод.
Решение:
Given expression: f(x) = x3 − 4x2 − 9x + 36 = 0.
Now, simply substitute random values for x in the graph for the given function:
x
-4
-3
-2
-1
0
1
2
3
4
5
f(x)
-56
0
19
40
36
24
10
0
0
16
We can see that the graph has cut the X-axis at 3 points, therefore, there are 3 real solutions.
From the graph, the solutions are: x = -3, x = 3, and x = 4.
Hence, the roots of the given equation are -3, 3, and 4.
Задачи на решение кубического уравнения
Задача 1: найти корни f(x) = x 3 – 4x 2 -3x + 6 = 0.
Решение:
Given expression: f(x) = x3 – 4x2 -3x + 6 = 0.
First, factorize the polynomial to get roots.
Since the constant is +6 the possible factors are 1, 2, 3, 6.
f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0
f(2) = 8 – 16 – 6 + 6 ≠ 0
f(3) = 27 – 36 – 9 + 6 ≠ 0
f(6) = 216 – 144 -18 + 6 = -48 ≠ 0
So, (x – 1) is a factor of the given equation. Now to find the remaining factors use the synthetic division method.
So, f(x) = x3 – 4x2 -3x + 6 = (x – 1) (x2 – 3x – 6) = 0
We know that the roots of a quadratic equation ax2 + bx + c = 0 are,
x = [-b ± √(b2-4ac)]/2a
x = [3 ± √(32 – 4(1)(-6)]/2(1)
x = (3 ± √33)/2
Hence, the roots of the given cubic equation are 1, (3+√33)/2, and (3–√33)/2.
Задача 2: найти корни уравнения f(x) = 4x 3 – 10x 2 + 4x = 0.
Решение:
Given expression: f(x) = 4x3 – 10x2 + 4x = 0
⇒ x (4x2 – 10x + 4) = 0
⇒ x (4x2 – 8x – 2x + 4) = 0
⇒ x(4x(x – 2) – 2(x – 2)) = 0
⇒ x (4x – 2) (x – 2) = 0
⇒ x = 0 or 4x – 2 = 0, x – 2 = 0
⇒ x = 0 or x = 1/2 or x = 2
Hence, the roots of the given equation are 0, 1/2 and 2.
Задача 3: найти корни уравнения f(x) = x 3 + 3x 2 + x + 3 = 0.
Решение:
Given expression: f(x) = x3 + 3x2 + x + 3 = 0.
⇒ x2 (x + 3) + 1(x + 3) = 0
⇒ (x + 3) (x2 + 1) = 0
⇒ x + 3 = 0 or x2 + 1 = 0
⇒ x = -3, ±i
So, the given equation has a real root, i.e., -3, and two imaginary roots, i.e., ±i.
Задача 4: найти корни уравнения f(x) = x 3 – 3x 2 – 5x + 7 = 0.
Решение:
Given expression: f(x) = x3 – 3x2 – 5x + 7 = 0.
First, factorize the polynomial to get roots.
Since the constant is +7 the possible factors are 1 and 7.
f(1) = 1 – 3 – 5 + 7 = 0
f(7) = 343 – 147 – 35 + 7 ≠ 0
So, (x – 1) is a factor of the given equation. Now to find the remaining factors use synthetic the division method.
So, f(x) = x3 – 3x2 – 5x + 7 = (x – 1) (x2 – 2x – 7) = 0
We know that the roots of a quadratic equation ax2 + bx + c = 0 are,
x = [-b ± √(b2-4ac)]/2a
x = [2 ± √(22–4(1)(-7)]/2(1)
= (2 ± √30)/2
Hence, the roots of the given cubic equation are 1, (2+√30)/2, and (2–√30)/2.
Задача 5. Найдите корни уравнения f(x) = x 3 − 6x 2 + 11x − 6 = 0, используя графический метод.
Решение:
Given expression: f(x) = x3 − 6x2 + 11x − 6 = 0.
Now, simply substitute random values for x in the graph for the given function:
x
1
2
3
4
5
f(x)
0
0
0
6
24
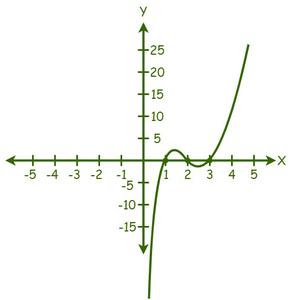
We can see that the graph has cut the X-axis at 3 points, therefore, there are 3 real solutions.
From the graph, the solutions are: x = 1, x = 2, and x = 3.
Hence, the roots of the given equation are 1, 2, and 3.