Реализация локально взвешенной линейной регрессии

LOESS или LOWESS - это методы непараметрической регрессии, которые объединяют несколько моделей регрессии в метамодель на основе k-ближайших соседей. LOESS сочетает в себе большую часть простоты линейной регрессии наименьших квадратов с гибкостью нелинейной регрессии. Это достигается путем подгонки простых моделей к локализованным подмножествам данных для создания функции, описывающей изменение данных по пунктам.

• Этот алгоритм используется для прогнозирования, когда между функциями существует нелинейная связь.
• Локально взвешенная линейная регрессия - это алгоритм обучения с учителем.
• Это непараметрический алгоритм.
• doneThere существует Нет фазы обучения. Вся работа выполняется на этапе тестирования / при составлении прогнозов.

Предположим, мы хотим оценить функцию гипотезы h в определенной точке запроса x . Для линейной регрессии мы бы сделали следующее:

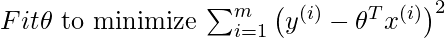
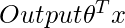
Вместо этого для локально взвешенной линейной регрессии мы сделаем следующее:

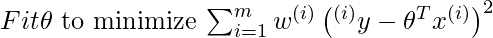
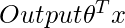
где w(i) - это неотрицательный «вес», связанный с тренировочной точкой x(i) . Более высокое «предпочтение» отдается точкам обучающей выборки, лежащим в окрестности x чем точкам, лежащим далеко от x . поэтому для x(i) лежащего ближе к точке запроса x , значение w(i) велико, а для x(i) лежащего далеко от x значение w(i) мало.
w(i) можно выбрать как -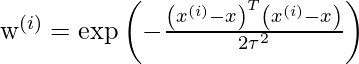

Непосредственно используя решение закрытой формы для поиска параметров -

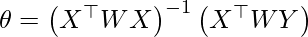
Код: Импорт библиотек:

import numpy as np import matplotlib.pyplot as plt import pandas as pd plt.style.use( "seaborn" )

Код: загрузка данных:

# Loading CSV files from local storage dfx = pd.read_csv( 'weightedX_LOWES.csv' ) dfy = pd.read_csv( 'weightedY_LOWES.csv' ) # Getting data from DataFrame Object and storing in numpy n-dim arrays X = dfx.values Y = dfy.values

Выход:

Код: Функция для расчета матрицы весов:

# function to calculate W weight diagnal Matric used in calculation of predictions def get_WeightMatrix_for_LOWES(query_point, Training_examples, Bandwidth): # M is the No of training examples M = Training_examples.shape[ 0 ] # Initialising W with identity matrix W = np.mat(np.eye(M)) # calculating weights for query points for i in range (M): xi = Training_examples[i] denominator = ( - 2 * Bandwidth * Bandwidth) W[i, i] = np.exp(np.dot((xi - query_point), (xi - query_point).T) / denominator) return W

Код: Прогнозы:

# function to make predictions def predict(training_examples, Y, query_x, Bandwidth): M = Training_examples.shape[ 0 ] all_ones = np.ones((M, 1 )) X_ = np.hstack((training_examples, all_ones)) qx = np.mat([query_x, 1 ]) W = get_WeightMatrix_for_LOWES(qx, X_, Bandwidth) # calculating parameter theta theta = np.linalg.pinv(X_.T * (W * X_)) * (X_.T * (W * Y)) # calculating predictions pred = np.dot(qx, theta) return theta, pred

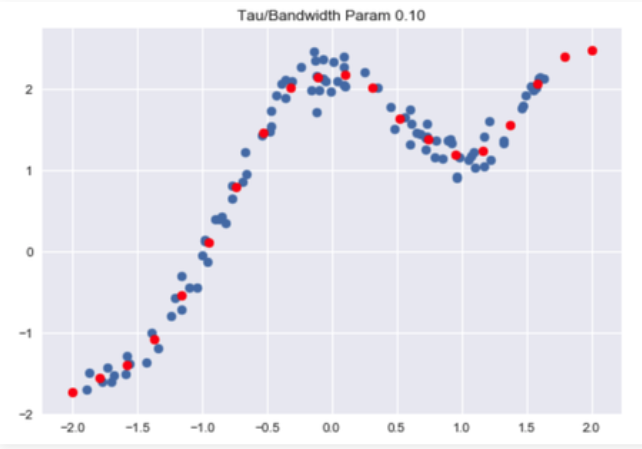
Код: Визуализируйте прогнозы:

# visualise predicted values with respect # to original target values Bandwidth = 0.1 X_test = np.linspace( - 2 , 2 , 20 ) Y_test = [] for query in X_test: theta, pred = predict(X, Y, query, Bandwidth) Y_test.append(pred[ 0 ][ 0 ]) horizontal_axis = np.array(X) vertical_axis = np.array(Y) plt.title( "Tau / Bandwidth Param %.2f" % Bandwidth) plt.scatter(horizontal_axis, vertical_axis) Y_test = np.array(Y_test) plt.scatter(X_test, Y_test, color = 'red' ) plt.show()

Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.