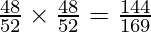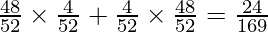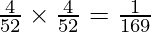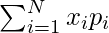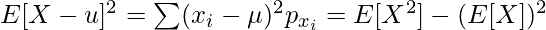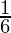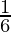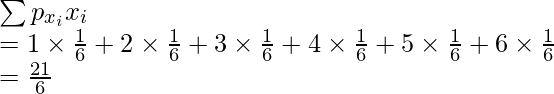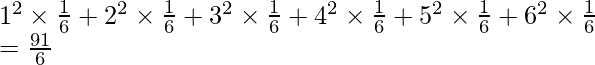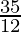Распределение вероятностей

Распределение вероятностей для случайной переменной показывает, как вероятности распределяются для различных значений случайной переменной. Когда все значения случайной переменной выровнены на графике, значения ее вероятностей образуют форму. Распределение вероятности имеет несколько свойств (например, ожидаемое значение и отклонение), которые можно измерить.

В распределении вероятностей результат случайной переменной является неопределенным. Здесь наблюдение результата известно как Осознание. Это функция, которая отображает пространство выборки в пространство вещественных чисел, известное как пространство состояний. Они могут быть дискретными или непрерывными.

Случайные переменные

Случайная переменная - важное понятие в вероятности и статистике. Нам нужно понимать это интуитивно и математически, чтобы глубже понять распределения вероятностей, которые окружают нас в повседневной жизни.

It’s a function which associates a real number with an event. 

Иногда нас интересуют не только вероятности событий в экспериментах, но и некоторые числа, связанные с экспериментом. Вот когда мы чувствуем потребность в случайных величинах.

Возьмем пример подбрасывания монеты. Начнем с того, что подбросим монетку и узнаем. Мы будем использовать H для обозначения орла и T для обозначения решки.

Итак, теперь мы подбрасываем монету 5 раз и хотим ответить на несколько вопросов.

1. What is the probability of getting exactly 3 heads?

2. What is the probability of getting less than 4 heads?

3. What is the probability of getting more than 1 head?

Тогда наш общий способ написания был бы следующим:

· P(Probability of getting exactly 3 heads when we flip a coin 5 times)

· P(Probability of getting less than 4 heads when we flip a coin 5 times)

· P(Probability of getting more than 1 head when we flip a coin 5 times) 

В другом сценарии предположим, что мы бросаем две кости и нам интересно узнать вероятность получения двух чисел, сумма которых равна 6.

Итак, в обоих случаях нам на помощь приходят случайные величины. Во-первых, давайте математически определим, что такое случайная величина.

Определение

Это присвоение значения (числа) каждому возможному результату. Говоря более математически, это функция от пространства отсчетов Ω до действительных чисел. Мы можем выбрать нашу случайную переменную в соответствии с нашими потребностями.

A random variable is a real valued function whose domain is the sample space of a random experiment

Чтобы сделать это более интуитивно понятным, давайте рассмотрим эксперимент с подбрасыванием монеты два раза подряд.

Примерное пространство эксперимента S = {HH, HT, TH, TT} . Давайте определим случайную переменную для подсчета событий орла или решки в соответствии с нашими потребностями, пусть X обозначает количество полученных голов. Для каждого результата его значения приведены ниже:

X(HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0.

В одном и том же пространстве выборки можно определить более одной случайной величины. Например, пусть Y обозначает количество голов за вычетом количества решек для каждого результата вышеприведенного выборочного пространства S.

 Y(HH) = 2, Y (HT) = 0, Y (TH) = 0, Y (TT) = – 2

Таким образом, X и Y - две разные случайные величины, определенные для одной и той же выборки.

Note: More than one event can map to same value of random variable. 

Типы случайных величин в вероятностном распределении

• Дискретные случайные переменные
• Непрерывные случайные переменные

Дискретные случайные величины в вероятностном распределении

Дискретная случайная величина может принимать только конечное число значений. Чтобы лучше понять это, давайте рассмотрим несколько примеров дискретных случайных величин:

1. X = {сумма результатов при выпадении двух кубиков}. Здесь X может принимать только такие значения, как {2, 3, 4, 5, 6… .10, 11, 12}.
2. X = {Количество голов в 100 бросках монеты}. Здесь X может принимать только целые значения из [0,100].

Непрерывная случайная переменная в распределении вероятностей

Непрерывная случайная величина может принимать бесконечные значения в непрерывной области. Давайте посмотрим на пример игры в дартс.

Предположим, у нас есть игра в дротики, в которой мы бросаем дротик, при этом дротик может упасть в любом месте между [-1,1] по оси x. Итак, если мы определим нашу случайную переменную как x-координату положения дротика, X может принимать любое значение из [-1,1]. X может принимать бесконечно много возможных значений. (X = {0,1, 0,001, 0,01, 1,2, 2,112121…. И так далее}.

Распределение вероятностей случайной величины

Теперь возникает вопрос, как описать поведение случайной величины?

Предположим, что наша случайная величина принимает только конечные значения, такие как x ₁ , x ₂ , x ₃ …. и x _n . То есть диапазон X - это набор из n значений {x ₁ , x ₂ , x ₃ …. и x _n }.

Таким образом, поведение X полностью описывается заданием вероятностей для всех значений случайной величины X

Функция вероятности дискретной случайной величины X - это функция p (x), удовлетворяющая

р (х) = Pr (Х = х)

Давайте посмотрим на пример:

Вопрос: Мы тянем две карты подряд с заменой из хорошо перетасованной колоды из 52 карт. Найдите распределение вероятностей нахождения тузов.

Отвечать:

Let’s define a random variable “X”, which means number of aces. So since we are only drawing two cards form the deck, X can only take three values: 0, 1 and 2.  We also know that, we are drawing cards with replacement which means that the two draws can be considered an independent experiments. 

P(X = 0) = P(both cards are non-aces) 

               = P(non-ace) x P(non-ace) 

               = 

P(X = 1) = P(one of the cards in ace) 

               = P(non-ace and then ace) + P(ace and then non-ace)

               = P(non-ace) x P(ace) + P(ace) x P(non-ace)

               = 

P(X = 2) = P(Both the cards are aces) 

               = P(ace) x P(ace)

               = 

Now we have probabilities for each value of random variable. Since it is discrete, we can make a table to represent this distribution. The table is given below. 

Икс	0	1	2
Pr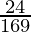

Ожидание (среднее) и дисперсия случайной переменной

Предположим, у нас есть вероятностный эксперимент, который мы проводим, и мы определили некоторую случайную величину (RV) в соответствии с нашими потребностями (как мы это делали в некоторых предыдущих примерах). Теперь, каждый раз, когда проводится эксперимент, наша RV принимает другое значение. Но мы хотим знать, что если мы продолжим эксперимент тысячу раз или бесконечное количество раз, каким будет среднее значение случайной величины?

Ожидание

Среднее, ожидаемое значение или ожидание случайной величины X записывается как E ( X ) или . Если мы наблюдаем N случайных значений X , то среднее из N значений будет примерно равно E (X) для больших N.

For a random variable X which takes on values x₁, x_2, x_{3 …} x_n with probabilities  p₁, p₂, p₃ … p_n. Expectation of X is defined as, 

i.e it is weighted average of all values which X can take, weighted by the probability of each value. 

Чтобы увидеть это более интуитивно, давайте взглянем на этот график ниже,

Теперь на приведенном выше рисунке мы видим, что обе случайные величины имеют почти одинаковое «среднее», но означает ли это, что они равны? Нет. Чтобы полностью описать свойства / поведение случайной величины, нам нужно нечто большее, верно?

Нам нужно посмотреть на дисперсию распределения вероятностей: одно из них сосредоточено, а другое сильно разбросано около одного значения. Итак, нам нужна метрика для измерения дисперсии на графике.

Дисперсия

В статистике мы выяснили, что дисперсия является мерой разброса или разброса данных. Точно так же изменчивость или разброс значений случайной величины можно измерить дисперсией.

For a random variable X which takes on values x₁, x₂, x₃ … x_n with probabilities  p₁, p₂, p₃ … p_n and the expectation is  E[X] 

The variance of X or Var(X) is denoted by, 

Давайте вычислим среднее значение и дисперсию распределения вероятностей случайной величины на примере:

Вопрос: Найдите дисперсию и среднее значение числа, полученного при броске несмещенной кости.

Отвечать:

We know that the sample space of this experiment is {1,2,3,4,5,6} 

Let’s define our random variable X, which represents the number obtained on a throw. 

So, the probabilities of the values which our random variable can take are, 

P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 

Therefore, the probability distribution of the random variable is, 

X	1	2	3	4	5	6
Probabilities

E[X] = 

Also, E[X²] = 

Thus, Var(X) = E[X²] – (E[X])²

                      = 

So, therefore mean is and variance is 

Различные типы вероятностных распределений

Мы видели, что такое вероятностные распределения, теперь мы увидим разные типы вероятностных распределений. Тип распределения вероятностей определяется типом случайной величины. Есть два типа вероятностных распределений:

• Дискретные распределения вероятностей для дискретных переменных
• Функции плотности вероятности для непрерывных переменных

Мы подробно изучим два типа дискретных распределений вероятностей, другие выходят за рамки класса 12.

Дискретные распределения вероятностей

Дискретные функции вероятности предполагают дискретное количество значений. Например, подбрасывание монет и подсчет событий являются дискретными функциями. Это дискретные распределения, потому что нет промежуточных значений. При подбрасывании монеты у нас может быть либо орел, либо решка.

Для дискретных функций распределения вероятностей каждое возможное значение имеет ненулевую вероятность. Более того, вероятности всех значений случайных величин должны в сумме равняться единице. Например, вероятность выпадения определенного числа на кубике равна 1/6. Полная вероятность для всех шести значений равна единице. Когда мы бросаем кубик, мы получаем только одно из этих значений.

Испытания Бернулли и биномиальные распределения

Многие эксперименты имеют только один из двух результатов. Например, подброшенная монета показывает «голову» или «хвост», изготовленный предмет может быть «дефектным» или «исправным». В этих случаях мы можем назвать один из этих результатов «успехом», а другой - «неудачей». Скажем, в эксперименте с подбрасыванием монеты, если появление головы считается успешным, то появление хвоста считается неудачей.

Каждый раз, когда мы подбрасываем монету, бросаем кубик или проводим любой другой эксперимент, мы называем это испытанием. Теперь мы знаем, что в наших экспериментах по подбрасыванию монеты результат любого исследования не зависит от результата любого другого исследования. В каждом из таких испытаний вероятность успеха или неудачи остается постоянной. Такие независимые испытания, которые имеют только два исхода, обычно называемые «успехом» или «неудачей», называются испытаниями Бернулли.

Определение:

Trials of the random experiment are known as Bernoulli trials, if they are satisfying below given conditions :

• Finite number of trials are required.
• All trials must be independent.
• Every trial has two outcomes : success or failure.
• Probability of success remains  same in every trial.

Давайте возьмем пример эксперимента, в котором мы бросаем кубик, бросание кубика 50 раз можно рассматривать как случай из 50 испытаний Бернулли, где результатом каждого испытания является либо успех (предположим, что получение четного числа - успех), либо неудача ( точно так же получение нечетного числа - неудача), и вероятность успеха (p) одинакова для всех 50 бросков. Очевидно, что последовательные броски кости - это независимые испытания. Если игральный кубик имеет шесть цифр от 1 до 6, написанных на шести гранях, то p = 1/2 и q = 1 - p = 1/2 = вероятность неудачи.

Вопрос: В урне находится 8 красных шаров и 10 черных шаров. Из урны последовательно вытягиваем шесть шаров. Вы должны определить, являются ли попытки вытягивания шаров испытаниями Бернулли, когда после каждой розыгрыша вытаскивается шар:

1. заменены
2. не заменяется в урне.

Отвечать:

• We know that the number of trials are finite. When drawing is done with replacement, probability of success (say, red ball) is p =8/18 which will be same for all of the six trials. So, drawing of balls with replacements are Bernoulli trials.
• If  drawing is done without replacement,  probability of success (i.e., red ball) in the first trial is 8/18 , in 2nd trial is 7/17 if  first ball drawn is red or, 10/18 if  first ball drawn is black, and so on. Clearly, probabilities of success are not same for all the trials, Therefore, the trials are not Bernoulli trials.

Биномиальное распределение

Это случайная величина, которая представляет количество успехов в «N» последовательных независимых испытаниях эксперимента Бернулли. Он используется во множестве случаев, таких как включение числа орлов при подбрасывании монеты «N» и так далее.

Пусть P и Q обозначают успех и неудачу в испытании Бернулли. Предположим, мы заинтересованы в поиске различных способов достижения одного успеха во всех шести испытаниях.

Ясно, что доступны шесть случаев, перечисленных ниже:

PQQQQQ, QPQQQQ, QQPQQQ, QQQPQQ, QQQQPQ, QQQQQP

Точно так же 2 успеха и 4 неудачи покажут комбинации. Так много комбинаций очень сложно перечислить. Отныне вычисление вероятностей 0, 1, 2,…, n успехов может быть долгим и трудоемким. Чтобы избежать таких длинных вычислений вместе со списком всех возможных случаев, для вероятностей количества успехов в испытаниях n-Бернулли составляется формула:

Если Y - биномиальная случайная величина, мы обозначаем это Y∼ Bin (n, p), где p - вероятность успеха в данном испытании, q - вероятность неудачи, Пусть n - общее количество следов и «x» - количество успехов. Биномиальная случайная величина имеет следующие свойства:

P (Y) = ⁿ C _x q ^{n – x} p ^x

Теперь функция вероятности P (Y) известна как функция вероятности биномиального распределения.

Вопрос: Когда честная монета подбрасывается 10 раз, вероятность:

1. ровно шесть голов
2. минимум шесть голов

Ответ :

Every coin tossed can be considered as the Bernoulli trial . Suppose X be the number of heads in this experiment: 

We already know, n = 10

                            p = 1/2

So, P(X = x) = ⁿC_x p^n-x (1-p)^x , x= 0,1,2,3,….n

P(X = x) = ¹⁰C_xp^10-x(1-p)^x  

When x = 6, 

(i) P(x = 6) = ¹⁰C₆ p⁴ (1-p)⁶

                   = 

(ii) P(at least 6 heads) = P(X >= 6) = P(X = 6) + P(X=7) + P(X=8)+ P(X=9) + P(X=10) 

= ¹⁰C₆ p⁴ (1-p)⁶ + ¹⁰C₇ p³ (1-p)⁷ + ¹⁰C₈ p² (1-p)⁸ + ¹⁰C₉ p¹(1-p)⁹ + ¹⁰C₁₀ (1-p)¹⁰ =