Расчет в MATLAB

Исчисление важно в различных областях, таких как инженерия, физика и другие науки, но расчеты выполняются машинами или компьютерами, независимо от того, относятся ли они к физике или технике. Здесь используется инструмент MATLAB, язык программирования, используемый инженерами и учеными для анализа данных. Итак, в этой статье подробно обсуждается исчисление с помощью MATLAB.

Пределы в MATLAB

Поскольку все мы знаем, что концепция исчисления начинается с пределов, давайте кратко вспомним предел. Мы помним график с линией, что в ней дырка, сначала это казалось странным, но потом казалось нормальным, раньше было обозначение, которое раньше выглядело так, оно читается как предел f(x) как x приближается к некоторому числу.

В этом случае число равно 1. X приближается к единице, и с левой стороны графика мы можем видеть и записывать значения y по мере того, как x приближается к 1.

График здесь для лучшей визуализации

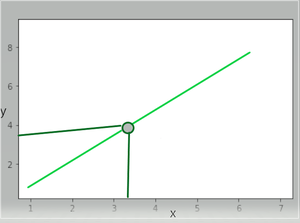
Теперь давайте рассмотрим функцию f(x)=x^2+x+4, и вы хотите узнать предел, когда x приближается к 4.

Пример:

Выход:

Теперь давайте возьмем некоторые тригонометрические функции, пусть функция будет sin(x)-cos(x)/cos2x, когда x приближается к pi/4.

Пример:

Выход:

ans =  -1/√2  

Дифференциация в MATLAB

Дифференцирование — это процесс нахождения производной функции по переменной, под производной понимается скорость изменения функции по переменной. Мы применяли дифференцирование, чтобы найти скорость в физике и других областях. Производные — это функции, которые сообщают нам наклон линии, касательной к кривой в любой точке. В dy/dx переменная y дифференцируется по x. Давайте посмотрим на следующий график.

Есть наклон и зеленая линия, давайте назовем эту секущую линию, теперь, если мы хотим найти расстояние между двумя точками линии, мы будем использовать формулу наклона, то есть m = (y2-y1/x2- х1). В этом случае координаты (x, f(x)) и (f(x+h),f(x)), наклон будет разностным фактором, учитывая цифру, но это всего лишь приближение, мы не нужно приближение, нам нужно точное решение, нам нужно приблизиться к x от начала секущей или, скажем, нам нужно минимизировать h, нам нужно, чтобы h было равно нулю, и когда h равно нулю и линия становится касательной кривой, мы берем предел разностного отношения.

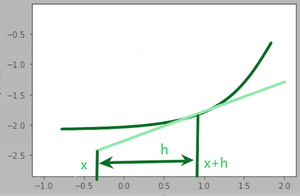
Этот метод нахождения производных называется нахождением производных при заданном пределе.

Давайте посмотрим на несколько примеров, касающихся производных алгебраических функций.

Пример:

Выход:

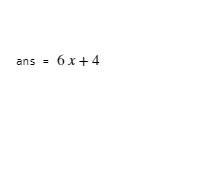
Если мы хотим дифференцировать экспоненциальные функции, то

Пример:

Выход:

Здесь используется правило произведения, т.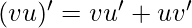

Интеграция в MATLAB

Интегралы, также называемые антипроизводными, отвечают за нахождение площади под кривой, понятие интегрирования можно понять по следующему графику

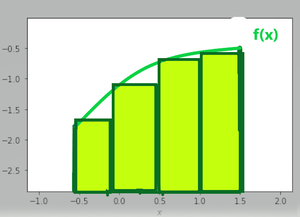
Приведенный выше график имеет кривую, и если мы хотим найти площадь под этой кривой, то здесь следует подход, кривая заполнена прямоугольниками, сумма прямоугольников будет площадью кривой, но проблема в том, есть много пустого пространства, мы обозначаем его Δx, но мы все еще можем заполнить кривую большим количеством прямоугольников,

Как мы видим, Δx действительно уменьшается, но чтобы его полностью исключить, нам нужно больше прямоугольника,

Таким образом, если заполнить достаточно прямоугольника или ширина прямоугольника приблизится к нулю по ширине, Δx станет dx, и мы получим ответ. Поскольку мы обсуждали, что интегралы являются обратными производными, интегрирование 2x будет равно x^2, а дифференцирование x^2 будет равно 2x. Теперь давайте посмотрим на некоторые примеры интегралов, кстати, интеграл показан или представлен ∫ этим символом.

Давайте посмотрим, как интегрировать алгебраическое выражение в MATLAB.

Пример:

Выход:

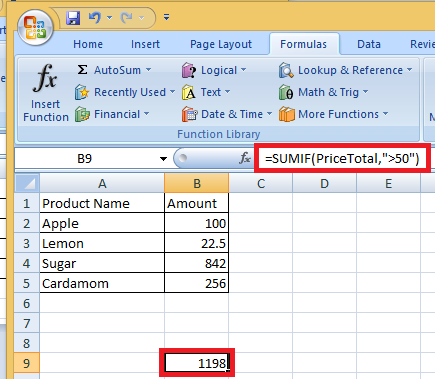
Давайте посмотрим на некоторые продвинутые концепции исчисления.

Векторное исчисление

Векторы имеют как величину величины, так и направление, они имеют величину и, безусловно, они будут течь в каком-то направлении, точно так же, если мы идем, они будут двигаться в определенном направлении. Концепция векторной алгебры широко используется в STEM. Но зачем нам интегрировать или дифференцировать векторы, ведь когда дело доходит до решения дифференциальных уравнений в частных производных, потока жидкости или гравитационных кошачьих, это полезно, поэтому, если мы интегрируем или дифференцируем вектор, мы интегрируем оси X и Y отдельно .

Скручивание и расходимость векторного поля

Curl and Divergence, также известный как язык уравнений Максвелла, потока жидкости и т. д.; но чтобы понять их, давайте визуализируем текущую откуда-то жидкость и визуализируем электромагнитное поле. Теперь, используя понятие дивергенции, мы можем определить поток жидкости, расширяющейся в данной точке, дивергенция является скейлерной величиной, а не вектором, так как она определяет скорость расширения жидкости в точке, так как здесь нет участия направление, это скалярная величина, чтобы найти расхождение векторного поля в трехмерном пространстве, мы выполняем скалярное произведение оператора частной производной (также вызывающего град) на поле, математически пусть F будет векторным полем в трехмерном пространстве и пусть x,y,z - его координаты, тогда дивергенция векторного поля будет

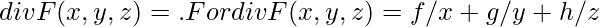
В случае положительной дивергенции поток направлен наружу, подобно расширяющемуся горячему газу, в случае отрицательной дивергенции рассматривается случай сжатия холодного газа. Чтобы визуализировать эту концепцию, представьте, что вы наполняете воздушный шар воздухом, воздушный шар надувается, это единственный пример, где можно визуализировать положительное расхождение.

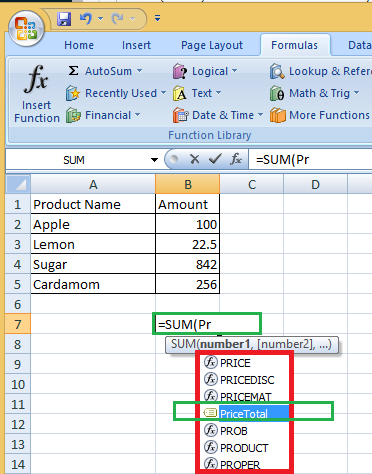
Теперь посмотрим, как найти расхождение в MATLAB.

Выход:

Теперь посмотрим на Curl, если нам нужно найти циркуляцию вектора в трехмерном пространстве, то мы будем использовать Curl, это плотность циркуляции в каждой точке поля. Предположим, что есть вектор с тремя измерениями, тогда ротор вектора будет

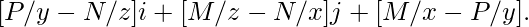
Чтобы сделать то же самое в MATLAB, предположим, что V является векторным полем относительно вектора X, причем оба они имеют три измерения. Пусть V = [x^3+y^3+z, y^3+x^3+z, z^3+x^3+y] и X = [x,y,z].

Выход:

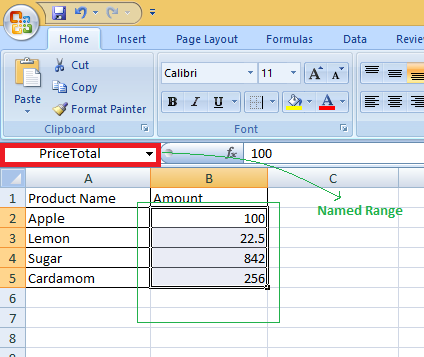
Завиток и дивергенция, также называемые языком электромагнитных уравнений Максвелла, набора связанных дифференциальных уравнений в частных производных вместе с законом силы Лоренца, составляют основы электродинамики.

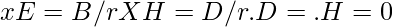
Где E — электрическое поле, B — магнитное поле, H — напряженность магнитного поля, а ρ — плотность заряда.

Градиент в MATLAB

Градиент используется для определения того, насколько резко поднимается или опускается линия или наклон, обычный метод дифференцирования дает нам скорость изменения функции только с одной переменной, но что, если функция имеет две переменные (например, f(x ,y)), то приходит понятие градиента, пусть функция

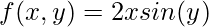
Таким образом, градиент f (x, y) будет векторной формой частного дифференциала по x и y.

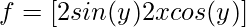
Геометрический смысл градиента

Предположим, вы взбираетесь на гору и хотите знать путь, по которому вы хотите быстро добраться до вершины горы, или если вы просто хотите обогнуть гору (быть на той же высоте, не поднимаясь и не вниз), то с помощью градиента мы увидим это. Давайте посмотрим контурные графики здесь,

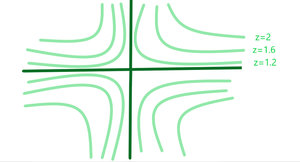
Приведенный выше рисунок представляет собой двумерную проекцию Контуров на трехмерную плоскость, поэтому использование концепции градиента и ее построение дает нам решение этой горной проблемы.

Серия Тейлора

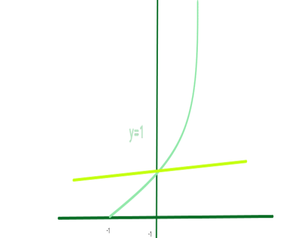
Ряд Тейлора — одна из важнейших теорем всего исчисления. Чтобы это понять, рассмотрим функцию e^x при x=0, она равна 1, а как узнать, когда x равно 0,2, будем аппроксимировать, будет ошибка, но незначительная , но когда x будет равен 1,2, погрешность будет велика, посмотрим на график ниже

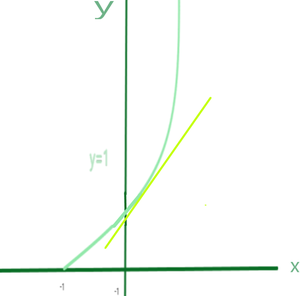
Мы видим постоянную функцию, но с помощью аппроксимации мы можем использовать линейную аппроксимацию, график будет выглядеть примерно так

Но мы можем добиться большего, чем это, для аппроксимации, на самом деле изучение ряда Тейлора состоит в том, чтобы брать неполиномиальные функции и находить полиномы, которые приближаются к некоторым входным данным, поскольку полиномы являются действительно удобными функциями, когда дело доходит до их интегрирования или дифференцирования, поэтому нам нужно чтобы найти функцию, которая лучше всего соответствует нашему экспоненциальному графику вблизи x = 0.

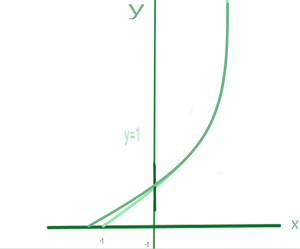
Полиномиальная функция при x = 0 равна T1 = x ^ 4/24 + x ^ 3/6 + x ^ 2/2 + x + 1.

Давайте посмотрим, как сделать аппроксимацию Тейлора в MATLAB.

Выход:

Вышеприведенный код имеет ту же экспоненциальную функцию, что и показанная на графике, и выдаст результат. Приближение Тейлора используется в инженерных областях, статистике, физике и информатике.