Программа на Java для оптимизации длины провода в электрической цепи
Даны n электрических компонентов и m электрических проводов для их соединения, каждый из которых имеет длину. Найдите оптимальную длину провода между двумя компонентами.
Пример :
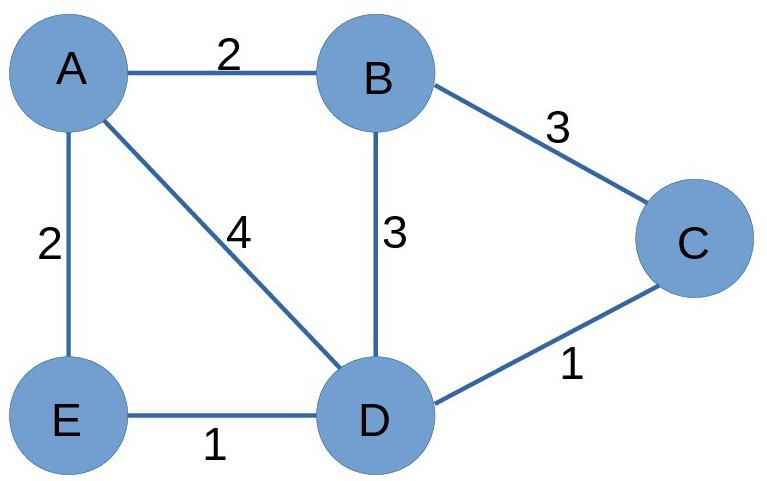
Input : Source = A
Destination = C
Output: 4
Explanation: There are five different paths from node A to node C i.e., A->B->C, A->B->D->C, A->D->C, A->E->D->C, A->D->B->C. But the path with smallest or optimized length is A->E->D->C with length as 4.
Подход :
Данные n компонентов и m проводов составляют неориентированный взвешенный граф. Задача состоит в том, чтобы рассчитать оптимальную длину между двумя компонентами, т. Е. Минимальную длину между двумя компонентами. Проблема заключается в применении алгоритма Дейкстры. Поскольку источник доступен, наименьшую длину от источника до всех узлов можно рассчитать с помощью алгоритма Дейкстры. Это даст минимально возможную длину между данным источником узла и всеми другими узлами в виде массива. Теперь с помощью этого массива можно указать самую короткую длину от источника до места назначения. Давайте разберемся в этом на примере.
Пример :
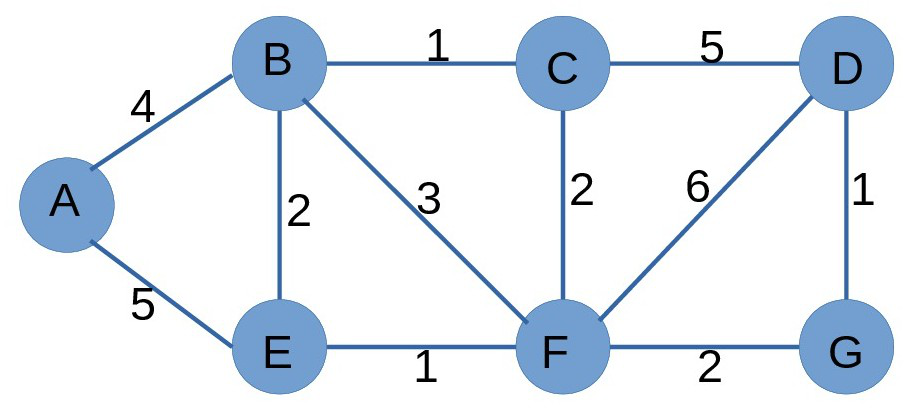
Input: Source = A
Destination = D
Output: 9
Explanation: Use Dijkstra’s algorithm to calculate shortest length from source A to all other nodes.
Vertex Distance from source
A 0
B 4
C 5
D 9
E 5
F 6
G 8
The shortest length can be found for any component from source A. Final answer will be the shortest length from A to D i.e., 9.
Below is the implementation of the above approach:
Java
// Java program for implementation// of above approachimport java.util.*; class GFG { // n is no. of nodes and m is no. of edges public static int n, m; // adjacency list representation of graph public static List<List<Node> > graph = new ArrayList<List<Node> >(); // source and destination points for shortest path public static int src, dest; static class Node { // node"s label public int label; // length of edge to this node public int length; public Node(int v, int w) { label = v; length = w; } } // Driver program public static void main(String[] args) throws Exception { n = 5; m = 7; // Initialize adjacency list structure // to empty lists: for (int i = 0; i <= n; i++) { List<Node> item = new ArrayList<Node>(); graph.add(item); } graph.get(1).add(new Node(2, 2)); graph.get(2).add(new Node(1, 2)); graph.get(1).add(new Node(4, 4)); graph.get(4).add(new Node(1, 4)); graph.get(1).add(new Node(5, 2)); graph.get(5).add(new Node(1, 2)); graph.get(4).add(new Node(5, 1)); graph.get(5).add(new Node(4, 1)); graph.get(2).add(new Node(4, 3)); graph.get(4).add(new Node(2, 3)); graph.get(2).add(new Node(3, 3)); graph.get(3).add(new Node(2, 3)); graph.get(4).add(new Node(3, 1)); graph.get(3).add(new Node(4, 1)); // Source node src = 1; // Destination node dest = 3; dijkstra(); } // Function to implement Dijkstra"s algorithm public static void dijkstra() { // array to keep track of unvisited nodes boolean[] done = new boolean[n + 1]; // node array to keep track of path // from source to all other nodes Node[] table = new Node[n + 1]; // intialise all nodes for (int i = 1; i <= n; i++) table[i] = new Node(-1, Integer.MAX_VALUE); // source to source length is 0 table[src].length = 0; // Dijkstra"s algorithm implementation for (int count = 1; count <= n; count++) { int min = Integer.MAX_VALUE; int minNode = -1; // find the minimum length node // from unvisited nodes for (int i = 1; i <= n; i++) { if (!done[i] && table[i].length < min) { min = table[i].length; minNode = i; } } // visit the minNode done[minNode] = true; // iterator to traverse all connected // nodes to minNode ListIterator iter = graph.get(minNode).listIterator(); while (iter.hasNext()) { Node nd = (Node)iter.next(); int v = nd.label; int w = nd.length; // update the distance from minNode // of unvisited nodes if (!done[v] && table[minNode].length + w < table[v].length) { table[v].length = table[minNode].length + w; table[v].label = minNode; } } } // length is now available rom source to all nodes System.out.println("Wire froms " + dest + " to " + src + " with length " + table[dest].length); int next = table[dest].label; System.out.print("Path is : " + dest + " "); // path from destination to source via all // intermediate nodes with minimum length while (next >= 0) { System.out.print(next + " "); next = table[next].label; } System.out.println(); }} |
Wire froms 3 to 1 with length 4 Path is : 3 4 5 1
Сложность по времени : Сложность по времени для приведенной выше реализации алгоритма Дейкстры составляет O (n ^ 2).
Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .
Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.