Программа для подсчета количества связанных компонентов в неориентированном графе

Опубликовано: 23 Января, 2022

Для неориентированного графа g задача состоит в том, чтобы вывести количество связанных компонентов в графе.

Примеры:

Input:

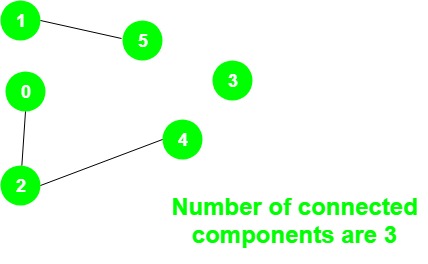
Output: 3
There are three connected components:
1 – 5, 0 – 2 – 4 and 3

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: идея состоит в том, чтобы использовать счетчик переменных для хранения количества подключенных компонентов и выполнить следующие шаги:

Инициализировать все вершины как непосещенные.
Для всех вершин проверьте, не была ли вершина посещена, затем выполните DFS для этой вершины и увеличьте счетчик переменных на 1.

Below is the implementation of the above approach:

C++

// C++ program for above approach
#include <bits/stdc++.h>
using namespace std;
 
// Graph class represents a undirected graph
// using adjacency list representation
class Graph {
    // No. of vertices
    int V;
 
    // Pointer to an array containing adjacency lists
    list<int>* adj;
 
    // A function used by DFS
    void DFSUtil(int v, bool visited[]);
 
public:
    // Constructor
    Graph(int V);
 
    void addEdge(int v, int w);
    int NumberOfconnectedComponents();
};
 
// Function to return the number of
// connected components in an undirected graph
int Graph::NumberOfconnectedComponents()
{
 
    // Mark all the vertices as not visited
    bool* visited = new bool[V];
 
    // To store the number of connected components
    int count = 0;
    for (int v = 0; v < V; v++)
        visited[v] = false;
 
    for (int v = 0; v < V; v++) {
        if (visited[v] == false) {
            DFSUtil(v, visited);
            count += 1;
        }
    }
 
    return count;
}
 
void Graph::DFSUtil(int v, bool visited[])
{
 
    // Mark the current node as visited
    visited[v] = true;
 
    // Recur for all the vertices
    // adjacent to this vertex
    list<int>::iterator i;
 
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFSUtil(*i, visited);
}
 
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}
 
// Add an undirected edge
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w);
    adj[w].push_back(v);
}
 
// Driver code
int main()
{
    Graph g(5);
    g.addEdge(1, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 4);
 
    cout << g.NumberOfconnectedComponents();
 
    return 0;
}

Java

// Java program for above approach
import java.io.*;
import java.util.*;
 
public class ConnectedComponentCount
{
     
    private int v;
    private int e;
    private Map<Integer,
                HashSet<Integer>> adjMap;
    private static Map<Integer,
                       Integer> visited;
     
    ConnectedComponentCount(int vertices)
    {
        v = vertices;
        adjMap = new HashMap<Integer,
                        HashSet<Integer>>();
        visited = new HashMap<Integer,
                                  Integer>();
    }
     
    // Function to add edges
    private void addEdge(int s, int d)
    {
        adjMap.putIfAbsent(s,
                     new HashSet<Integer>());
        adjMap.putIfAbsent(d,
                     new HashSet<Integer>());
        adjMap.get(s).add(d);
        adjMap.get(s).add(s);
        adjMap.get(d).add(s);
        adjMap.get(d).add(d);
        visited.put(s, 0);
        visited.put(d, 0);
    }
     
    // To mark vertices which can be visites
    private void findDFS(int vertex)
    {
         
        // Mark as visited
        visited.put(vertex,1);
       
        // Print the vertex
        System.out.println("vertex " + vertex +
                                   " visited");
        for(Integer child : adjMap.get(vertex))
        {
            if(visited.get(child) == 0){
               findDFS(child);
            }
        }
    }
     
    // Function to print graph
    private void printGraph()
    {
        for(HashSet<Integer> v :
                          adjMap.values())
        {
            System.out.println(v.toString());
        }
    }
     
    // Driver Code
    public static void main(String args[])
    {
         
        Scanner sc = new Scanner(System.in);
        System.out.println("Enter the number
                           of vertices (V): ");
        int vertices = sc.nextInt();
         
        System.out.println("Enter the number
                                of edges (E): ");
        int edges = sc.nextInt();
         
        // To count total number of
        // components
        int ccCount = 0;
         
        ConnectedComponentCount ccc =
                 new ConnectedComponentCount(
                                      vertices);
         
        // Input of edges
        while (edges > 0)
        {
            System.out.println("Enter the
                                nodes s & d: ");
            int s = sc.nextInt();
            int d = sc.nextInt();
            ccc.addEdge(s,d);
            edges-- ;
        }
         
        // Function to print graph                     
        ccc.printGraph();
         
        // Traversing every node
        for(Integer vertex : visited.keySet())
        {
             
            // Check if vertex is already
            // visited  or not
            if(visited.get(vertex) == 0)
            {
                 
                // Function Call for findDFS
                ccc.findDFS(vertex);
               
                // Print Component Found
                System.out.println("CC Found");
               
                // Increase the counter
                ccCount++;
            }
        }
         
        // Print number of components                       
        System.out.println("Number of cc component: "
                                        + ccCount);
    }
}
 
//The code is contributed by Alfred Skaria

Python3

# Python3 program for above approach
 
# Graph class represents a undirected graph
# using adjacency list representation
class Graph:
     
    def __init__(self, V):
 
        # No. of vertices
        self.V = V
 
        # Pointer to an array containing
        # adjacency lists
        self.adj = [[] for i in range(self.V)]
 
    # Function to return the number of
    # connected components in an undirected graph
    def NumberOfconnectedComponents(self):
         
        # Mark all the vertices as not visited
        visited = [False for i in range(self.V)]
         
        # To store the number of connected
        # components
        count = 0
         
        for v in range(self.V):
            if (visited[v] == False):
                self.DFSUtil(v, visited)
                count += 1
                 
        return count
         
    def DFSUtil(self, v, visited):
 
        # Mark the current node as visited
        visited[v] = True
 
        # Recur for all the vertices
        # adjacent to this vertex
        for i in self.adj[v]:
            if (not visited[i]):
                self.DFSUtil(i, visited)
                 
    # Add an undirected edge
    def addEdge(self, v, w):
         
        self.adj[v].append(w)
        self.adj[w].append(v)
         
# Driver code       
if __name__=="__main__":
     
    g = Graph(5)
    g.addEdge(1, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 4)
     
    print(g.NumberOfconnectedComponents())
 
# This code is contributed by rutvik_56

Output

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Структуры данных

Программа для подсчета количества связанных компонентов в неориентированном графе

C++

Java

Python3

РЕКОМЕНДУЕМЫЕ СТАТЬИ