Проблема самого широкого пути | Практическое применение алгоритма Дейкстры

Опубликовано: 12 Января, 2022

Настоятельно рекомендуется сначала прочитать алгоритм Дейкстры, используя приоритетную очередь.
Проблема самого широкого пути - это проблема поиска пути между двумя вершинами графа, максимизирующего вес ребра с минимальным весом в пути . См. Изображение ниже, чтобы понять проблему:

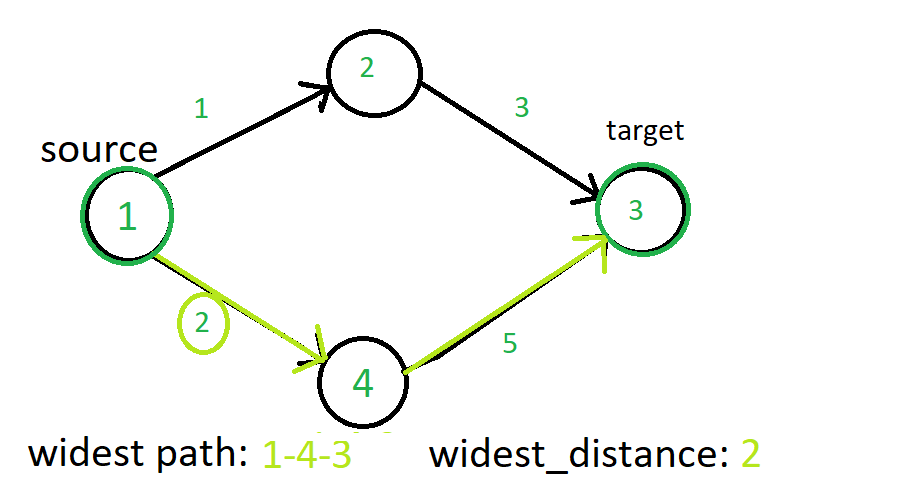
Пример практического применения:
Эта проблема является известным вариантом алгоритма Дейкстры. В практическом применении эту проблему можно рассматривать как граф с маршрутизаторами, поскольку его вершины и ребра представляют собой полосу пропускания между двумя вершинами. Теперь, если мы хотим найти путь с максимальной пропускной способностью между двумя точками подключения к Интернету, эту проблему можно решить с помощью этого алгоритма.
Как решить эту проблему?
Мы собираемся решить эту проблему, используя реализацию алгоритма Дейкстры с очередью приоритетов ((| E | + | V |) log | V |) с небольшими изменениями.
Мы решаем эту проблему, просто заменяя условие релаксации в алгоритме Дейкстры на:

max(min(widest_dist[u], weight(u, v)), widest_dist[v])

где u - исходная вершина для v. v - текущая вершина, в которой мы проверяем условие.
Этот алгоритм работает как для ориентированного, так и для неориентированного графа.
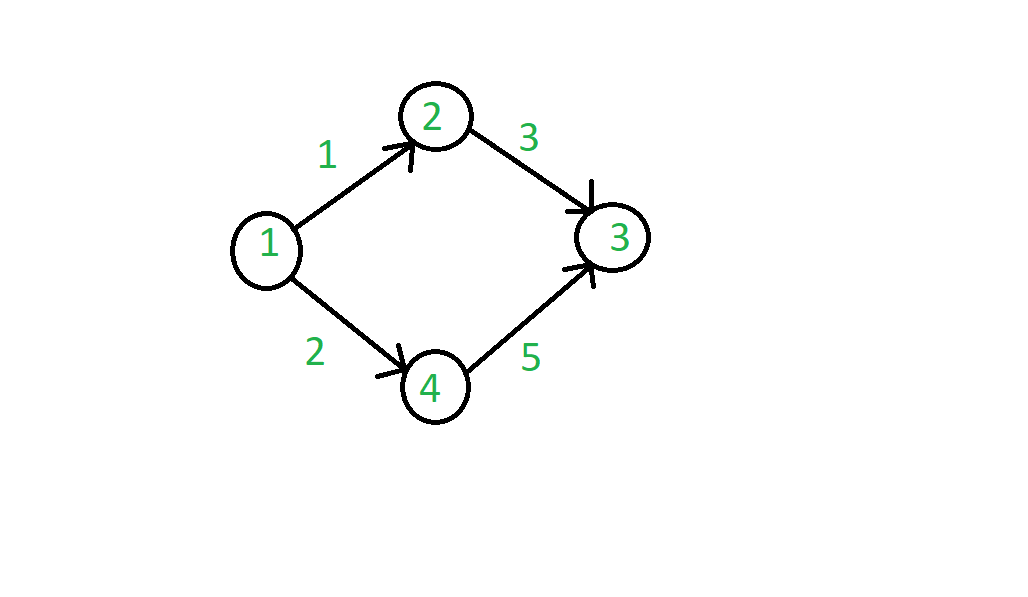
Посмотрите серию изображений ниже, чтобы получить представление о проблеме и алгоритме:
Значения по краям представляют собой веса направленных краев.

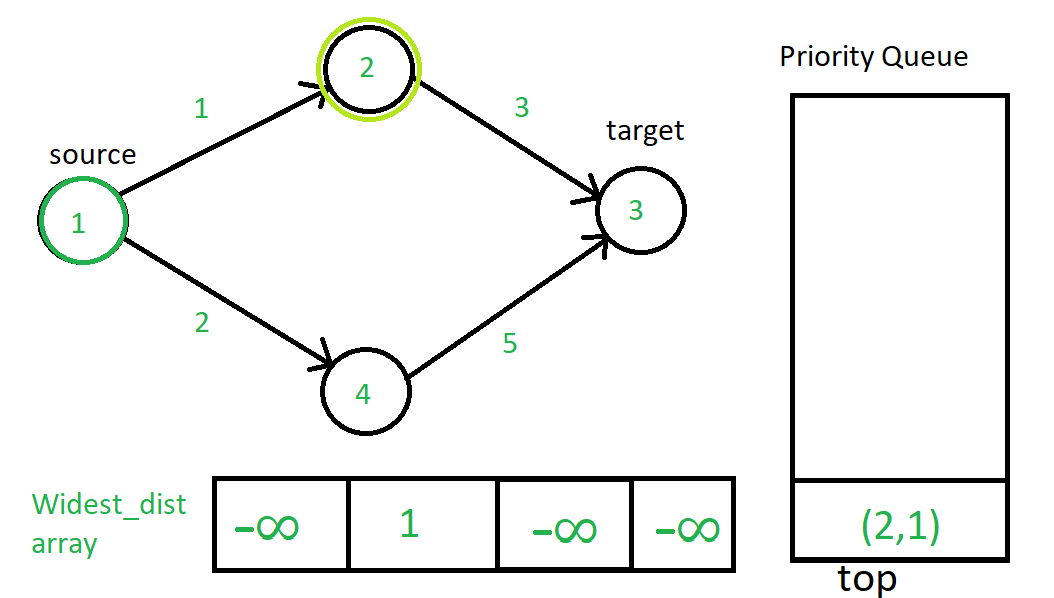
Мы начнем с исходной вершины, а затем проедем все вершины, соединенные с ней, и добавим приоритетную очередь в соответствии с условием релаксации.

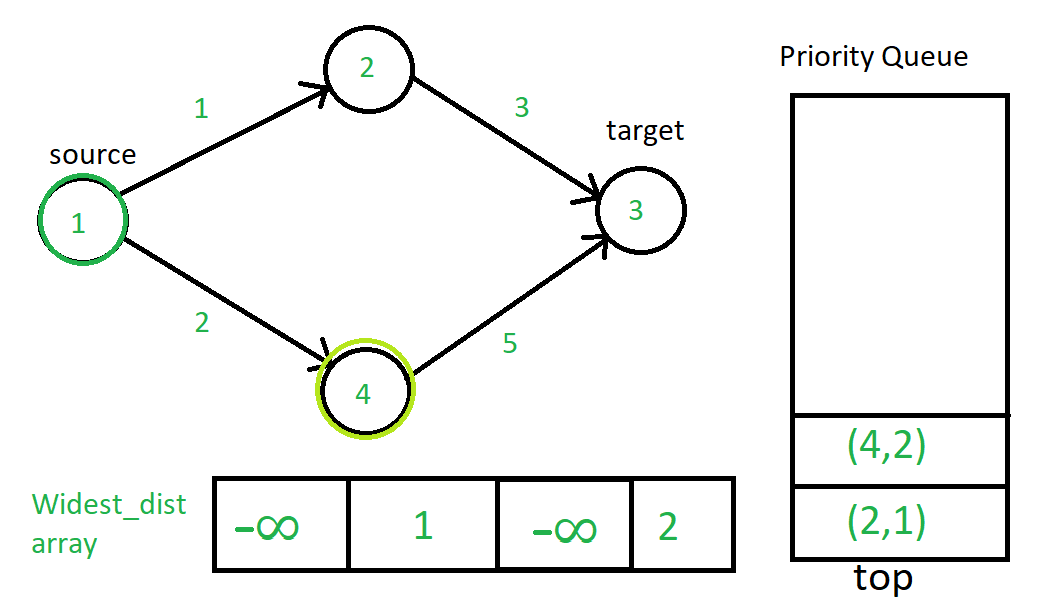
Теперь (2, 1) появится, и 2 будет текущей исходной вершиной.

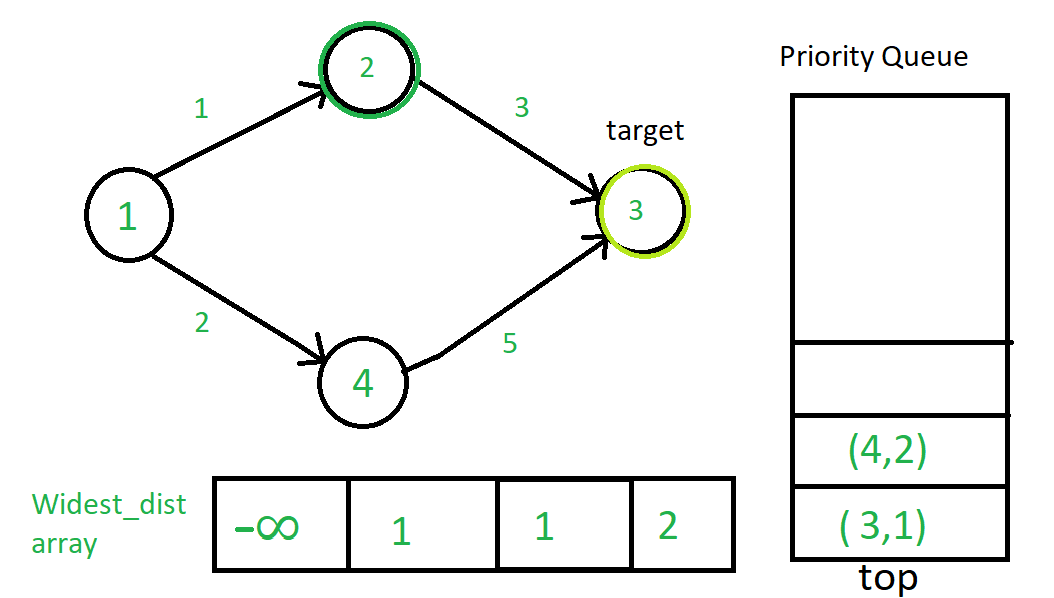
Теперь (3, 1) выскочит из очереди. Но поскольку 3 не имеет связной вершины через направленное ребро, ничего не произойдет. Итак, (4, 2) появится следующим.

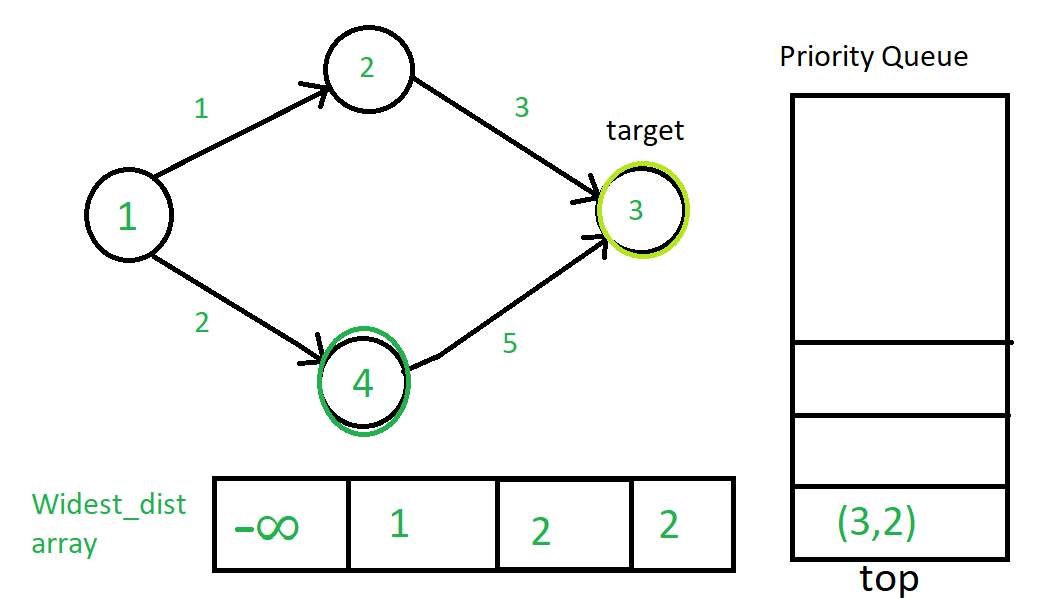
Наконец, алгоритм останавливается, поскольку в очереди с приоритетами больше нет элементов.

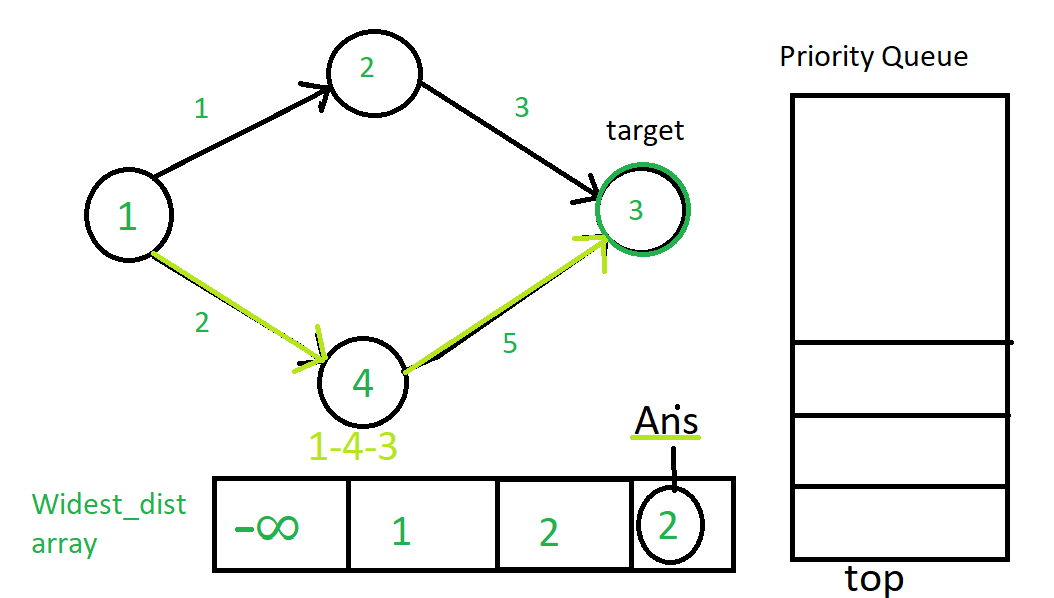
The path with the maximum value of widest distance is 1-4-3 which has the maximum bottle-neck value of 2. So we end up getting widest distance of 2 to reach the target vertex 3.
Below is the implementation of the above approach:

CPP

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to print the required path
void printpath(vector<int>& parent, int vertex, int target)
{
    if (vertex == 0) {
        return;
    }
 
    printpath(parent, parent[vertex], target);
 
    cout << vertex << (vertex == target ? "
" : "--");
}
 
// Function to return the maximum weight
// in the widest path of the given graph
int widest_path_problem(vector<vector<pair<int, int> > >& Graph,
                        int src, int target)
{
    // To keep track of widest distance
    vector<int> widest(Graph.size(), INT_MIN);
 
    // To get the path at the end of the algorithm
    vector<int> parent(Graph.size(), 0);
 
    // Use of Minimum Priority Queue to keep track minimum
    // widest distance vertex so far in the algorithm
    priority_queue<pair<int, int>, vector<pair<int, int> >,
                   greater<pair<int, int> > >
        container;
 
    container.push(make_pair(0, src));
 
    widest[src] = INT_MAX;
 
    while (container.empty() == false) {
        pair<int, int> temp = container.top();
 
        int current_src = temp.second;
 
        container.pop();
 
        for (auto vertex : Graph[current_src]) {
 
            // Finding the widest distance to the vertex
            // using current_source vertex"s widest distance
            // and its widest distance so far
            int distance = max(widest[vertex.second],
                               min(widest[current_src], vertex.first));
 
            // Relaxation of edge and adding into Priority Queue
            if (distance > widest[vertex.second]) {
 
                // Updating bottle-neck distance
                widest[vertex.second] = distance;
 
                // To keep track of parent
                parent[vertex.second] = current_src;
 
                // Adding the relaxed edge in the prority queue
                container.push(make_pair(distance, vertex.second));
            }
        }
    }
 
    printpath(parent, target, target);
 
    return widest[target];
}
 
// Driver code
int main()
{
 
    // Graph representation
    vector<vector<pair<int, int> > > graph;
 
    int no_vertices = 4;
 
    graph.assign(no_vertices + 1, vector<pair<int, int> >());
 
    // Adding edges to graph
 
    // Resulting graph
    // 1--2
    // |  |
    // 4--3
 
    // Note that order in pair is (distance, vertex)
    graph[1].push_back(make_pair(1, 2));
    graph[1].push_back(make_pair(2, 4));
    graph[2].push_back(make_pair(3, 3));
    graph[4].push_back(make_pair(5, 3));
 
    cout << widest_path_problem(graph, 1, 3);
 
    return 0;
}

Python3

# Python3 implementation of the approach
 
# Function to prthe required path
def printpath(parent, vertex, target):
     
    # global parent
    if (vertex == 0):
        return
    printpath(parent, parent[vertex], target)
    print(vertex ,end="
" if (vertex == target) else "--")
 
# Function to return the maximum weight
# in the widest path of the given graph
def widest_path_problem(Graph, src, target):
     
    # To keep track of widest distance
    widest = [-10**9]*(len(Graph))
 
    # To get the path at the end of the algorithm
    parent = [0]*len(Graph)
 
    # Use of Minimum Priority Queue to keep track minimum
    # widest distance vertex so far in the algorithm
    container = []
    container.append((0, src))
    widest[src] = 10**9
    container = sorted(container)
    while (len(container)>0):
        temp = container[-1]
        current_src = temp[1]
        del container[-1]
        for vertex in Graph[current_src]:
 
            # Finding the widest distance to the vertex
            # using current_source vertex"s widest distance
            # and its widest distance so far
            distance = max(widest[vertex[1]],
                           min(widest[current_src], vertex[0]))
 
            # Relaxation of edge and adding into Priority Queue
            if (distance > widest[vertex[1]]):
 
                # Updating bottle-neck distance
                widest[vertex[1]] = distance
 
                # To keep track of parent
                parent[vertex[1]] = current_src
 
                # Adding the relaxed edge in the prority queue
                container.append((distance, vertex[1]))
                container = sorted(container)
    printpath(parent, target, target)
    return widest[target]
 
# Driver code
if __name__ == "__main__":
 
    # Graph representation
    graph = [[] for i in range(5)]
    no_vertices = 4
    # Adding edges to graph
 
    # Resulting graph
    #1--2
    #|  |
    #4--3
 
    # Note that order in pair is (distance, vertex)
    graph[1].append((1, 2))
    graph[1].append((2, 4))
    graph[2].append((3, 3))
    graph[4].append((5, 3))
 
    print(widest_path_problem(graph, 1, 3))
 
# This code is contributed by mohit kumar 29

Output:

1--4--3
2

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Алгоритмы Структуры данных

Проблема самого широкого пути | Практическое применение алгоритма Дейкстры

CPP

Python3

РЕКОМЕНДУЕМЫЕ СТАТЬИ