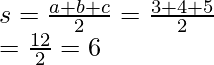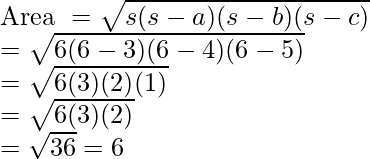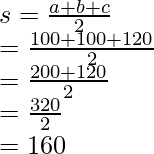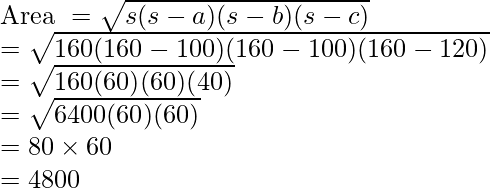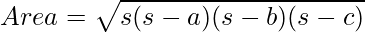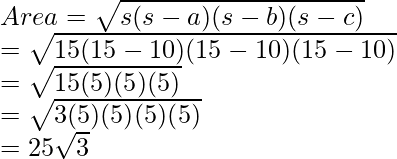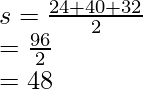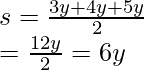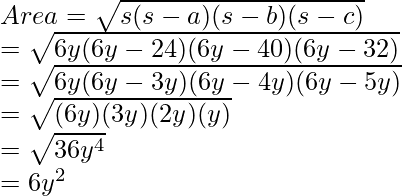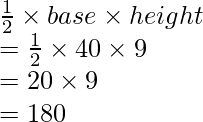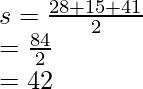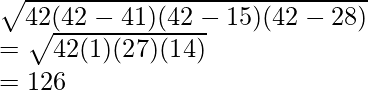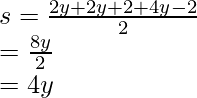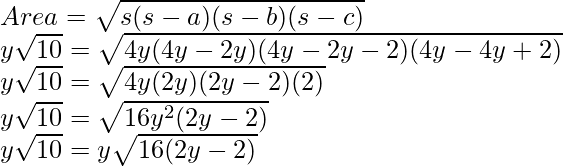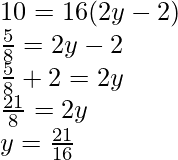Применение формулы Герона
При решении и нахождении площади треугольника ожидается, что некоторые параметры будут предоставлены заранее, например, должны быть доступны высота и основание треугольника. Или, в случае равностороннего треугольника, должны быть указаны длины сторон.
Площадь треугольника обычно определяется выражением
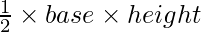
Где основание и высота отсчитываются от заданного треугольника. Но иногда может случиться так, что у нас нет этой информации. Предположим, у нас есть информация только о длине сторон. Высота неизвестна, как тогда будет рассчитываться площадь?
Ответом на этот вопрос является формула Герона.
Heron was born in Egypt in about 10AD. He was a great mathematician, he worked in applied mathematics. His great deal of work revolved around squares, rectangles. This formula is also called “Hero’s Formula”.
Формула Герона
Формула Герона также известна как формула Герона, она названа в честь очень известного инженера Египта. Он был известен и известен как «Герой Александрии». Его известные работы включают формулу Герона, торговый автомат и т. д. Лучшая часть о формула заключалась в том, что для определения площади любого треугольника не требовалось никакого угла или расстояния.
Допустим, у нас есть треугольник ABC, стороны которого имеют длины «a», «b» и «c».
Тогда площадь этого треугольника, данная Героном,
Площадь треугольника АВС 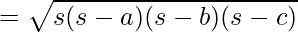
Где a, b и c - длина сторон, а s = полупериметр (половина периметра).
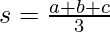
Эта формула позволяет вычислить площадь треугольника, где длина высоты не указана.
Применение формулы Герона для нахождения площади треугольников.
Формулу Герона можно использовать для нахождения площадей различных типов треугольников, если даны длины их сторон,
Вопрос: Найдите площадь треугольника, если его стороны равны 3, 5, 4.
Решение:
Area of this triangle can be calculated by Heron’s formula studied above,
Let’s calculate semi-perimeter first,
Plugging the values of s, a, b and c in the formula. Let’s calculate the area.
Thus, the area of the triangle is 6 square units.
Применение формулы Герона для нахождения площади четырехугольника
Мы знаем, как вычислить площадь стандартных четырехугольников, таких как прямоугольники, квадраты и трапеции. Но иногда может случиться так, что наши четырехугольники не находятся ни в одной из этих форм.

Приведенный выше четырехугольник не принадлежит ни к одной из этих категорий, поэтому наши стандартные формулы использовать нельзя. В таких случаях нам помогает формула Герона. Мы можем соединить любые две противоположные вершины на приведенном выше рисунке и сформировать два треугольника. Затем можно вычислить площадь. Давайте посмотрим на некоторые примеры по этому поводу.
Вопрос: Найдите площадь данного ромба по формуле Герона.

Решение:
There are two triangles here, both of them are similar.
The length of sides of both triangles are 100, 100 and 120.
Thus, semi perimeter for both the triangles is,
Now, calculating the area of the triangle
Thus, area of a single triangle is 4800. Since, there are two equal triangles. So, the total area is 9600 sq units.
Давайте посмотрим на некоторые примеры задач по этим понятиям,
Примеры задач на основе формулы Герона
Вопрос 1: Есть бетонное пространство в форме треугольника, которое нужно выложить плиткой. Стоимость укладки плитки 20 рублей за квадратный метр. Найдите общую стоимость облицовки площади.

Отвечать:
The length of given sides are 10, 10 and 10.
The semi-perimeter “s” = 15
We know the area of the triangle using Heron’s formula.
Here, s = 15, a = b = c = 10.
The area of the triangle is 25√3
So, the cost of tiling the area = 25√3 x 20
= 500√3
= 500 (1.73)
= 866 (approx)
Thus, cost of tiling the area is Rs. 866.
Вопрос 2: Длины сторон треугольника относятся как 3:5:4, а периметр равен 96м. Найдите площадь треугольника.
Решение:
The sides are in ratio of 3:5:4. Suppose the length of the sides is 3x,5x and 4x.
3x + 5x + 4x = 96
= 12x = 96
= x = 8.
Thus, the sides are 24, 40, 32. Now let’s calculate “s” and plug in the values in Heron’s formula.
Вопрос 3: Допустим, стороны треугольника равны 3y, 4y и 5y. Найдите выражение площади треугольника.
Отвечать:
Let’s find out the perimeter and semi perimeter so that we can plug in the values in Heron’s formula.
Plugging in the values in Heron’s Formula.
Вопрос 4: Найдите площадь четырехугольника, указанного ниже:

Решение:
The quadrilateral ABCD can be divided into two triangles whose area we can compute if we join A and C.
Now we have triangles ACD and ABC. Out of which ACD is a right-angled triangle.
AC2 = AD2 + DC2
⇒ AC2 = 92 + 402
⇒ AC2 = 81 + 1600
⇒ AC2 = 1681
⇒ AC = 41
Area of triangle ADC =
Area of triangle ABC will be calculated using Heron’s Formula. The sides of the triangle are 28,15 and 41.
Area of triangle ABC =
Area of quadrilateral = Area of triangle ADC + Area of triangle ABC
= 180 + 126
= 306 sq units.
Вопрос 5: Предположим, есть треугольник, стороны которого равны 2y, 2y + 2 и 4y – 2, а его площадь равна y√10. Узнайте значение у.
Решение:
Let’s calculate “s”
Comparing both sides of the equation,