Последовательность Аронсона

Опубликовано: 5 Января, 2022

Учитывая целое число 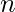, сгенерируйте первый 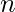условия последовательности Аронсона.

Последовательность Аронсона - это бесконечная последовательность целых чисел, полученная из индекса T (или t) в предложении:

“T is the first, fourth, eleventh, sixteenth, … letter in this sentence.”

Первое вхождение T в предложении находится в индексе 1 (индексация на основе 1), а номер, упомянутый первым, является первым, то есть 1
Точно так же второе вхождение t в предложении находится под индексом 4, а указанное второе число является четвертым, то есть 4
Точно так же третье вхождение t в предложении находится в индексе 11, а третье упомянутое число - одиннадцатое, то есть 11.
Точно так же серия продолжается как 1, 4, 11, 16,…

Примеры:

Input: n = 3
Output: 1, 4, 11
Input: n = 6
Output: 1, 4, 11, 16, 24, 29

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: простая идея - сохранить строку «T is the», чтобы получить первые два члена последовательности. Для каждого из этих терминов преобразуйте его в слова в порядковой форме, добавьте в строку и вычислите значение следующих более высоких терминов. Повторите этот процесс для каждого из последующих более высоких членов, сгенерированных n-2 раза, чтобы сгенерировать первые n членов последовательности Аронсона.
Чтобы преобразовать числа в слова, см. Здесь.

Ниже представлена реализация описанного выше подхода:

C ++

 // C++ program to generate the
 // first n terms of Aronson's sequence
 
#include <bits/stdc++.h>
 using namespace std;
 
// Returns the given number in words
 string convert_to_words(string num)
 {
 
    // Get number of digits in given number
    int len = num.length();
 
    // Base cases
    if (len == 0 || len > 4) {
        return "" ;
    }
    /*
      The following arrays contain
      one digit(both cardinal and ordinal forms),
      two digit(<20, ordinal forms) numbers,
      and multiples(ordinal forms) and powers of 10.
     
     */
    string single_digits_temp[]
        = { "" , "one" , "two" , "three" , "four"
              , "five" , "six" , "seven" , "eight" , "nine" };
    string single_digits[]
        = { "" , "first" , "second" , "third" , "fourth"
              , "fifth" , "sixth" , "seventh" , "eighth" , "ninth" };
 
    string two_digits[]
        = { "" , "tenth" , "eleventh" , "twelfth" , "thirteenth"
              , "fourteenth" , "fifteenth" , "sixteenth"
              , "seventeenth" , "eighteenth" , "nineteenth" };
 
    string tens_multiple[]
        = { "" , "tenth" , "twentieth" , "thirtieth" , "fortieth"
              , "fiftieth" , "sixtieth" , "seventieth"
              , "eightieth" , "ninetieth" };
 
    string tens_power[] = { "hundred" , "thousand" };
    string word = "" ;
 
    // If single digit number
    if (len == 1) {
        word += single_digits[num[0] - '0' ];
        return word;
    }
    int i = 0, ctr = 0;
    string s = " " ;
    while (i < len) {
 
        if (len >= 3) {
            if (num[i] != '0' ) {
                word
                    += single_digits_temp[num[i] - '0' ]
                       + " " ;
 
                // here len can be 3 or 4
                word += tens_power[len - 3] + " " ;
                ctr++;
            }
            len--;
            num.erase(0, 1);
        }
 
        // last two digits
        else {
            if (ctr != 0) {
                s = " and " ;
                word.erase(word.length() - 1);
            }
 
            // Handle all powers of 10
            if (num[i + 1] == '0' )
                if (num[i] == '0' )
                    word = word + "th" ;
                else
                    word += s + tens_multiple[num[i] - '0' ];
 
            // Handle two digit numbers < 20
            else if (num[i] == '1' )
                word += s + two_digits[num[i + 1] - '0' + 1];
 
            else {
                if (num[i] != '0' )
                    word
                        += s + tens_multiple[num[i] - '0' ]
                               .substr(0, tens_multiple[num[i] - '0' ]
                                  .length() - 4) + "y " ;
                else
                    word += s;
                word += single_digits[num[i + 1] - '0' ];
            }
            i += 2;
        }
        if (i == len) {
            if (word[0] == ' ' )
                word.erase(0, 1);
        }
    }
    return word;
 }
 
// Function to print the first n terms
 // of Aronson's sequence
 void Aronsons_sequence( int n)
 {
    string str = "T is the " ;
    int ind = 0;
    for ( int i = 0; i < str.length(); i++) {
 
        // check if character
        // is alphabet or not
        if ( isalpha (str[i])) {
            ind += 1;
        }
        if (str[i] == 't' or str[i] == 'T' ) {
            n -= 1;
 
            // convert number to words
            // in ordinal format and append
            str += convert_to_words(to_string(ind)) + ", " ;
            cout << ind << ", " ;
        }
        if (n == 0)
 
            break ;
    }
 }
 
// Driver code
 int main( void )
 {
    int n = 6;
    Aronsons_sequence(n);
    return 0;
 }

Джава

 // Java program to generate the
 // first n terms of Aronson's sequence
 import java.util.*;
 
class GFG
 {
 
// Returns the given number in words
 static String convert_to_words( char [] num)
 {
 
    // Get number of digits in given number
    int len = num.length;
 
    // Base cases
    if (len == 0 || len > 4 )
    {
        return "" ;
    }
     
    /*
    The following arrays contain
    one digit(both cardinal and ordinal forms),
    two digit(<20, ordinal forms) numbers,
    and multiples(ordinal forms) and powers of 10.
     
    */
    String single_digits_temp[]
        = { "" , "one" , "two" , "three" , "four"
            , "five" , "six" , "seven" , "eight" , "nine" };
    String single_digits[]
        = { "" , "first" , "second" , "third" , "fourth"
            , "fifth" , "sixth" , "seventh" , "eighth" , "ninth" };
 
    String two_digits[]
        = { "" , "tenth" , "eleventh" , "twelfth" , "thirteenth"
            , "fourteenth" , "fifteenth" , "sixteenth"
            , "seventeenth" , "eighteenth" , "nineteenth" };
 
    String tens_multiple[]
        = { "" , "tenth" , "twentieth" , "thirtieth" , "fortieth"
            , "fiftieth" , "sixtieth" , "seventieth"
            , "eightieth" , "ninetieth" };
 
    String tens_power[] = { "hundred" , "thousand" };
    String word = "" ;
 
    // If single digit number
    if (len == 1 )
    {
        word += single_digits[num[ 0 ] - '0' ];
        return word;
    }
     
    int i = 0 , ctr = 0 ;
    String s = " " ;
    while (i < len)
    {
 
        if (len >= 3 )
        {
            if (num[i] != '0' )
            {
                word
                    += single_digits_temp[num[i] - '0' ]
                    + " " ;
 
                // here len can be 3 or 4
                word += tens_power[len - 3 ] + " " ;
                ctr++;
            }
            len--;
            num=Arrays.copyOfRange(num, 1 , num.length);
        }
 
        // last two digits
        else
        {
            if (ctr != 0 )
            {
                s = " and " ;
                word = word.substring( 0 ,word.length() - 1 );
            }
 
            // Handle all powers of 10
            if (num[i + 1 ] == '0' )
                if (num[i] == '0' )
                    word = word + "th" ;
                else
                    word += s + tens_multiple[num[i] - '0' ];
 
            // Handle two digit numbers < 20
            else if (num[i] == '1' )
                word += s + two_digits[num[i + 1 ] - '0' + 1 ];
 
            else
            {
                if (num[i] != '0' )
                    word += s + tens_multiple[num[i] - '0' ]
                            .substring( 0 , tens_multiple[num[i] - '0' ]
                                .length() - 4 ) + "y " ;
                else
                    word += s;
                word += single_digits[num[i + 1 ] - '0' ];
            }
            i += 2 ;
        }
        if (i == len)
        {
            if (word.charAt( 0 ) == ' ' )
                word = word.substring( 1 ,word.length());
        }
    }
    return word;
 }
 
// Function to print the first n terms
 // of Aronson's sequence
 static void Aronsons_sequence( int n)
 {
    String str = "T is the " ;
    int ind = 0 ;
    for ( int i = 0 ; i < str.length(); i++)
    {
 
        // check if character
        // is alphabet or not
        if (Character.isAlphabetic(str.charAt(i)))
        {
            ind += 1 ;
        }
        if (str.charAt(i) == 't' || str.charAt(i) == 'T' )
        {
            n -= 1 ;
 
            // convert number to words
            // in ordinal format and append
            str += convert_to_words(String.valueOf(ind).toCharArray()) + ", " ;
            System.out.print(ind+ ", " );
        }
        if (n == 0 )
            break ;
    }
 }
 
// Driver code
 public static void main(String[] args)
 {
    int n = 6 ;
    Aronsons_sequence(n);
 }
 }
 
// This code is contributed by 29AjayKumar

C #

 // C# program to generate the
 // first n terms of Aronson's sequence
 using System;
 
class GFG
 {
 
// Returns the given number in words
 static String convert_to_words( char [] num)
 {
 
    // Get number of digits in given number
    int len = num.Length;
 
    // Base cases
    if (len == 0 || len > 4)
    {
        return "" ;
    }
     
    /*
    The following arrays contain
    one digit(both cardinal and ordinal forms),
    two digit(<20, ordinal forms) numbers,
    and multiples(ordinal forms) and powers of 10.
     
    */
    String []single_digits_temp
        = { "" , "one" , "two" , "three" , "four"
            , "five" , "six" , "seven" , "eight" , "nine" };
    String []single_digits
        = { "" , "first" , "second" , "third" , "fourth"
            , "fifth" , "sixth" , "seventh" , "eighth" , "ninth" };
 
    String []two_digits
        = { "" , "tenth" , "eleventh" , "twelfth" , "thirteenth"
            , "fourteenth" , "fifteenth" , "sixteenth"
            , "seventeenth" , "eighteenth" , "nineteenth" };
 
    String []tens_multiple
        = { "" , "tenth" , "twentieth" , "thirtieth" , "fortieth"
            , "fiftieth" , "sixtieth" , "seventieth"
            , "eightieth" , "ninetieth" };
 
    String []tens_power = { "hundred" , "thousand" };
    String word = "" ;
 
    // If single digit number
    if (len == 1)
    {
        word += single_digits[num[0] - '0' ];
        return word;
    }
     
    int i = 0, ctr = 0;
    String s = " " ;
    while (i < len)
    {
 
        if (len >= 3)
        {
            if (num[i] != '0' )
            {
                word
                    += single_digits_temp[num[i] - '0' ]
                    + " " ;
 
                // here len can be 3 or 4
                word += tens_power[len - 3] + " " ;
                ctr++;
            }
            len--;
            Array.Copy(num, 1, num, 0, num.Length - 1);

                    
                                            Статьи
                                    
РЕКОМЕНДУЕМЫЕ СТАТЬИОнлайн-обменники: быстрый и удобный способ конвертации активов в современном мире
17 Апреля, 2024
Лучшие онлайн-курсы по WordPress: рейтинг 2024
29 Марта, 2024
Для кого буду полезны услуги SMS-центра
24 Марта, 2024
Что такое экспертиза исходного кода и как ее проводят?
3 Марта, 2024
Как добавить деньги на счет аккаунта Steam через криптовалюту
20 Февраля, 2024
Заказать докторскую диссертацию на заказ
30 Января, 2024
Купить лайки в ВК: зачем, сколько и где
19 Января, 2024
Как добавить деньги на свой аккаунт в Steam и начать покупать игры и контент
12 Января, 2024

    


        
                    < PROGLER >

                

                    Общее
Контакты
Политика конфиденциальности

                    Обучение
Блог

                

                © progler.ru 2024. Все права защищены.
            

    