Поиск с равномерной стоимостью (Дейкстра для больших графов)

Опубликовано: 14 Января, 2022

Поиск с равномерной стоимостью - это вариант алгоритма Диджикстры. Здесь вместо того, чтобы вставлять все вершины в приоритетную очередь, мы вставляем только исходный код, а затем вставляем одну за другой, когда это необходимо. На каждом шаге мы проверяем, находится ли элемент уже в очереди приоритетов (используя массив посещений). Если да, то выполняем клавишу уменьшения, иначе вставляем.
Этот вариант Dijsktra полезен для бесконечных графов и тех графов, которые слишком велики для представления в памяти. Поиск по единообразной стоимости в основном используется в искусственном интеллекте.
Примеры:

 Вход :

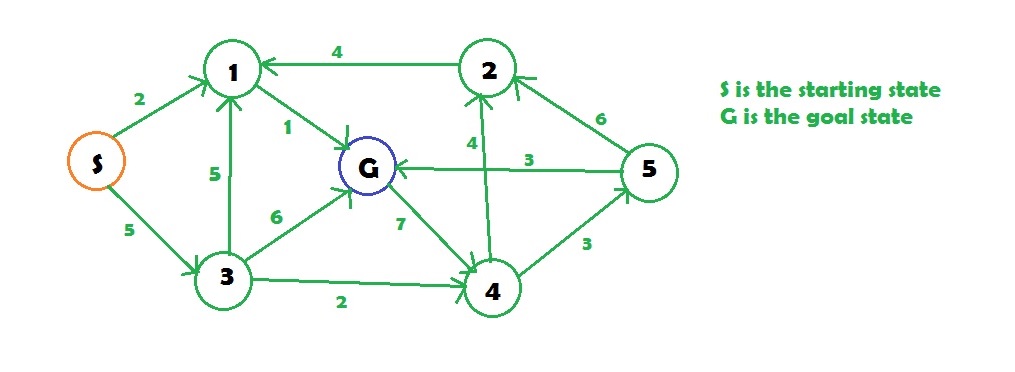
 Выход :
Минимальная стоимость от S до G = 3
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Uniform-Cost Search is similar to Dijikstra’s algorithm . In this algorithm from the starting state we will visit the adjacent states and will choose the least costly state then we will choose the next least costly state from the all un-visited and adjacent states of the visited states, in this way we will try to reach the goal state (note we wont continue the path through a goal state ), even if we reach the goal state we will continue searching for other possible paths( if there are multiple goals) . We will keep a priority queue which will give the least costliest next state from all the adjacent states of visited states .
 

CPP

// C++ implemenatation of above approach
#include <bits/stdc++.h>
using namespace std;
 
// graph
vector<vector<int> > graph;
 
// map to store cost of edges
map<pair<int, int>, int> cost;
 
// returns the minimum cost in a vector( if
// there are multiple goal states)
vector<int> uniform_cost_search(vector<int> goal, int start)
{
    // minimum cost upto
    // goal state from starting
    // state
    vector<int> answer;
 
    // create a priority queue
    priority_queue<pair<int, int> > queue;
 
    // set the answer vector to max value
    for (int i = 0; i < goal.size(); i++)
        answer.push_back(INT_MAX);
 
    // insert the starting index
    queue.push(make_pair(0, start));
 
    // map to store visited node
    map<int, int> visited;
 
    // count
    int count = 0;
 
    // while the queue is not empty
    while (queue.size() > 0) {
 
        // get the top element of the
        // priority queue
        pair<int, int> p = queue.top();
 
        // pop the element
        queue.pop();
 
        // get the original value
        p.first *= -1;
 
        // check if the element is part of
        // the goal list
        if (find(goal.begin(), goal.end(), p.second) != goal.end()) {
 
            // get the position
            int index = find(goal.begin(), goal.end(),
                             p.second) - goal.begin();
 
            // if a new goal is reached
            if (answer[index] == INT_MAX)
                count++;
 
            // if the cost is less
            if (answer[index] > p.first)
                answer[index] = p.first;
 
            // pop the element
            queue.pop();
 
            // if all goals are reached
            if (count == goal.size())
                return answer;
        }
 
        // check for the non visited nodes
        // which are adjacent to present node
        if (visited[p.second] == 0)
            for (int i = 0; i < graph[p.second].size(); i++) {
 
                // value is multiplied by -1 so that
                // least priority is at the top
                queue.push(make_pair((p.first +
                  cost[make_pair(p.second, graph[p.second][i])]) * -1,
                  graph[p.second][i]));
            }
 
        // mark as visited
        visited[p.second] = 1;
    }
 
    return answer;
}
 
// main function
int main()
{
    // create the graph
    graph.resize(7);
 
    // add edge
    graph[0].push_back(1);
    graph[0].push_back(3);
    graph[3].push_back(1);
    graph[3].push_back(6);
    graph[3].push_back(4);
    graph[1].push_back(6);
    graph[4].push_back(2);
    graph[4].push_back(5);
    graph[2].push_back(1);
    graph[5].push_back(2);
    graph[5].push_back(6);
    graph[6].push_back(4);
 
    // add the cost
    cost[make_pair(0, 1)] = 2;
    cost[make_pair(0, 3)] = 5;
    cost[make_pair(1, 6)] = 1;
    cost[make_pair(3, 1)] = 5;
    cost[make_pair(3, 6)] = 6;
    cost[make_pair(3, 4)] = 2;
    cost[make_pair(2, 1)] = 4;
    cost[make_pair(4, 2)] = 4;
    cost[make_pair(4, 5)] = 3;
    cost[make_pair(5, 2)] = 6;
    cost[make_pair(5, 6)] = 3;
    cost[make_pair(6, 4)] = 7;
 
    // goal state
    vector<int> goal;
 
    // set the goal
    // there can be multiple goal states
    goal.push_back(6);
 
    // get the answer
    vector<int> answer = uniform_cost_search(goal, 0);
 
    // print the answer
    cout << "Minimum cost from 0 to 6 is = "
         << answer[0] << endl;
 
    return 0;
}

Python3

# Python3 implemenatation of above approach
 
# returns the minimum cost in a vector( if
# there are multiple goal states)
def  uniform_cost_search(goal, start):
     
    # minimum cost upto
    # goal state from starting
    global graph,cost
    answer = []
 
    # create a priority queue
    queue = []
 
    # set the answer vector to max value
    for i in range(len(goal)):
        answer.append(10**8)
 
    # insert the starting index
    queue.append([0, start])
 
    # map to store visited node
    visited = {}
 
    # count
    count = 0
 
    # while the queue is not empty
    while (len(queue) > 0):
 
        # get the top element of the
        queue = sorted(queue)
        p = queue[-1]
 
        # pop the element
        del queue[-1]
 
        # get the original value
        p[0] *= -1
 
        # check if the element is part of
        # the goal list
        if (p[1] in goal):
 
            # get the position
            index = goal.index(p[1])
 
            # if a new goal is reached
            if (answer[index] == 10**8):
                count += 1
 
            # if the cost is less
            if (answer[index] > p[0]):
                answer[index] = p[0]
 
            # pop the element
            del queue[-1]
 
            queue = sorted(queue)
            if (count == len(goal)):
                return answer
 
        # check for the non visited nodes
        # which are adjacent to present node
        if (p[1] not in visited):
            for i in range(len(graph[p[1]])):
 
                # value is multiplied by -1 so that
                # least priority is at the top
                queue.append( [(p[0] + cost[(p[1], graph[p[1]][i])])* -1, graph[p[1]][i]])
 
        # mark as visited
        visited[p[1]] = 1
 
    return answer
 
# main function
if __name__ == "__main__":
     
    # create the graph
    graph,cost = [[] for i in range(8)],{}
 
    # add edge
    graph[0].append(1)
    graph[0].append(3)
    graph[3].append(1)
    graph[3].append(6)
    graph[3].append(4)
    graph[1].append(6)
    graph[4].append(2)
    graph[4].append(5)
    graph[2].append(1)
    graph[5].append(2)
    graph[5].append(6)
    graph[6].append(4)
 
    # add the cost
    cost[(0, 1)] = 2
    cost[(0, 3)] = 5
    cost[(1, 6)] = 1
    cost[(3, 1)] = 5
    cost[(3, 6)] = 6
    cost[(3, 4)] = 2
    cost[(2, 1)] = 4
    cost[(4, 2)] = 4
    cost[(4, 5)] = 3
    cost[(5, 2)] = 6
    cost[(5, 6)] = 3
    cost[(6, 4)] = 7
 
    # goal state
    goal = []
 
    # set the goal
    # there can be multiple goal states
    goal.append(6)
 
    # get the answer
    answer = uniform_cost_search(goal, 0)
 
    # print the answer
    print("Minimum cost from 0 to 6 is = ",answer[0])
 
# This code is contributed by mohit kumar 29

C#

// C# implemenatation of above approach
using System;
using System.Collections;
using System.Collections.Generic;
 
class GFG
{
 
// graph
static List<List<int>> graph=new List<List<int>>();
 
// map to store cost of edges
static Dictionary<Tuple<int,int>,int> cost= new Dictionary<Tuple<int,int>,int>();
 
// returns the minimum cost in a vector( if
// there are multiple goal states)
static List<int> uniform_cost_search(List<int> goal, int start)
{
    // minimum cost upto
    // goal state from starting
    // state
    List<int> answer=new List<int>();
 
    // create a priority queue
    List<Tuple<int, int> > queue = new List<Tuple<int, int> >();
 
    // set the answer vector to max value
    for (int i = 0; i < goal.Count; i++)
        answer.Add(int.MaxValue);
 
    // insert the starting index
    queue.Add(new Tuple<int,int>(0, start));
 
    // map to store visited node
    Dictionary<int, int> visited=new Dictionary<int,int>();
 
    // count
    int count = 0;
 
    // while the queue is not empty
    while (queue.Count > 0) {
 
        // get the top element of the
        // priority queue
        Tuple<int, int> q = queue[0];
        Tuple<int, int> p = new Tuple<int,int>(-q.Item1,q.Item2);
 
        // pop the element
        queue.RemoveAt(0);
 
 
        // check if the element is part of
        // the goal list
        if (goal.Contains(p.Item2)) {
 
            // get the position
            int index = goal.IndexOf(p.Item2);
 
            // if a new goal is reached
            if (answer[index] == int.MaxValue)
                count++;
 
            // if the cost is less
            if (answer[index] > p.Item1)
                answer[index] = p.Item1;
 
            // pop the element
            queue.RemoveAt(0);
 
            // if all goals are reached
            if (count == goal.Count)
                return answer;
        }
 
        // check for the non visited nodes
        // which are adjacent to present node
        if (!visited.ContainsKey(p.Item2))
            for (int i = 0; i < graph[p.Item2].Count; i++) {
 
                // value is multiplied by -1 so that
                // least priority is at the top
                queue.Add(new Tuple<int,int>((p.Item1 + (cost.ContainsKey(new Tuple<int,int>(p.Item2, graph[p.Item2][i])) ? cost[new Tuple<int,int>(p.Item2, graph[p.Item2][i])] : 0))*-1,
                graph[p.Item2][i]));
            }
 
        // mark as visited
        visited[p.Item2] = 1;
    }
 
    return answer;
}
 
// main function
public static void Main(params string []args)
{
    // create the graph
    graph=new List<List<int>>();
Алгоритмы Искусственный интеллект

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Революция в обработке фото: как нейросети меняют игру
26 Апреля, 2024
Midjourney: нейросеть, которая рисует по словам
18 Июля, 2023
Разница между жадным алгоритмом и алгоритмом «разделяй и властвуй»
14 Февраля, 2023
Сжатие и распаковка текстовых файлов с использованием кодирования Хаффмана
21 Января, 2023
Введение в амортизированный анализ
12 Января, 2023
Как анализировать сложность рекуррентного отношения
12 Января, 2023
Наихудший, средний и лучший анализ алгоритмов
4 Января, 2023
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022