По какому правилу вычитаются положительные числа?

Раздел математики, который имеет дело с арифметическими операциями и символами, которые их представляют, называется алгеброй. Алгебра охватывает широкий круг тем, от поиска решений простых уравнений до изучения абстракций. Алгебра помогает решать математические уравнения и позволяет вычислять неизвестные величины, такие как пропорции, скорость лодки и проценты. В алгебре объекты представлены буквами или другими символами для построения математического уравнения. В нашей повседневной жизни, используя алгебраические формулы, мы можем определить расстояние между двумя местами, вместимость контейнеров и скидки, когда они требуются.

Положительные числа

Числа играют решающую роль во всех аспектах нашей жизни, от поддержания порядка до подсчета элементов в списке, от подготовки ежемесячного бюджета до расчета ежемесячных расходов и многого другого. Существуют различные виды чисел, а именно положительные числа, отрицательные числа, четные числа, нечетные числа, простые числа, составные числа, последовательные числа, совершенные числа и т. д. Числа подразделяются на различные типы в зависимости от их свойств, и отрицательное число один из них. Перед положительным числом может стоять символ (+), или оно может быть просто числом, и его значение всегда больше нуля. Положительные числа отображаются справа от нуля в числовой строке. 2, 15, 23,86, 17/19 и т. д. являются некоторыми примерами положительных чисел, т. е. положительные числа могут быть целыми, десятичными или дробными.

Правила вычитания положительных чисел

Specific guidelines must be followed when we perform arithmetic operations like addition, subtraction, multiplication, and division on numbers. 

The rule for Subtraction

A positive number is subtracted from another by changing its sign, which is followed by adding the sign-changed number to the first number. However, the final output may be a positive or negative number and the magnitude of the result will be less than both operands if none of the operands is zero.

Case 1: Second operand > the first operand

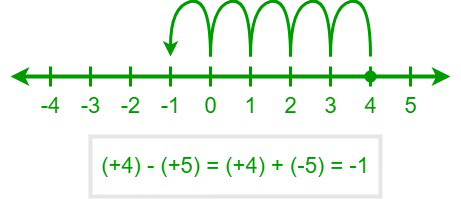
The final output will be a negative number if the magnitude of the second operand is greater than the first operand. For example, (+4) – (+5) will be equal to (+4) + (-5). We know that, on a number line, we shift to the left to add a negative number. So, as “–5” is added to (+4), we shift 5 units to the left, starting from (+4). Hence, the answer is “–1.”

 

Case 2: Second operand < the first operand

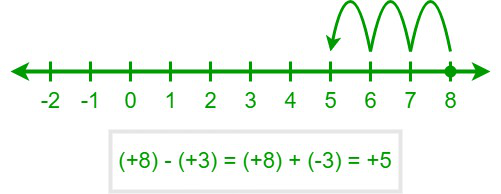
The final output will be a positive number if the magnitude of the second operand is less than the first operand. For example, +8 – (+3) will be equal to (+8) + (–3). We know that, on a number line, we shift to the left to add a negative number. So, as “–3” is added to (+8), we shift 3 units to the left, starting from (+8). Hence, the answer is “+5.”

 

Case 3: Second operand = the first operand

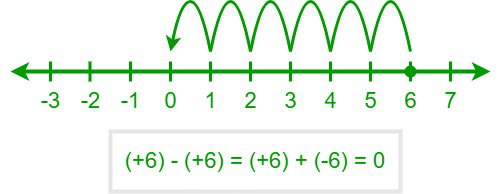
The final output will be zero if the magnitude of the second operand is equal to the first operand. For example, (+6) – (+6) will be equal to (+6) + (–6). We know that, on a number line, we shift to the left to add a negative number. So, as “–6” is added to (+6), we shift 6 units to the left, starting from (+6). Hence, the answer is “0.”

 

Примеры проблем

Задача 1: Найдите решение для: (3 × 4) — (2 × 5) — (1 × 8).

Решение:

Given,

(3 × 4) – (2 × 5) – (1 × 8)

By solving the bracket at first, we get

= (12) – (10) – (8)

Now, open the brackets.

= 12 – 10 – 8

Now, add the positive and negative integers separately.

= 12 – 18

= -6

Therefore, (3 × 4) – (2 × 5) – (1 × 8) = -6

Задача 2: вычесть 6a ² + 8b ² + 20ab из (3a + 5b) ² .

Решение:

Given,

(3a – 5b)² – (6a² + 8b² + 20ab)

= (9a² + 25b²+ 30ab) – (6a² + 8b² + 20ab) {Since, (a + b)² = a² + b² + 2ab}

Now, open the brackets,     

= 9a² + 25b² + 30ab – 6a² – 8b² – 20ab

Now, add or subtract like terms.

= 9a² – 6a² + 25b² – 8b² + 30ab – 20ab

= 3a² + 17b² + 10ab

Hence, (3a + 5b)² – (6a² + 8b² + 20ab) = 3a² + 17b² + 10ab

Задача 3: Оцените: 68 – 35 – 10 – 43 + 14.

Решение:

Given,

68 – 35 – 10 – 43 + 14

Add the positive and negative integers separately

= 68 + 14 – 35 – 10 – 43

= 82 – 88

= (+82) + (-88) = -6

Hence, [68 – 35 – 10 – 43 + 14] = -6

Задача 4: вычесть заданные положительные целые числа,

• Вычесть 10 из 5
• Вычесть 17 из 29
• Вычесть 56 из 87

Решение:

• Subtract 10 from 5 = (+5) – (+10)

From the rule of subtracting negative numbers, we know that, when a positive number is subtracted from another by changing its sign, which is followed by adding the sign-changed number to the first number.

Hence, (+5) – (+10) = (+5) + (–10) = –5

• Subtract 17 from 29 = (+29) – (+17)

= (+29) + (–17) = +12

• Subtract 56 from 87 = (+87) – (+56)

= (+87) + (–56) = +31

Задача 5. Вычесть (5x + 2y) ² из (7x + 6y) ² .

Решение:

Given,

(7x + 6y)² – (5x + 2y)²

=  (49x² + 36y² + 84xy) – (25x² + 4y² + 20xy)       {Since, (a + b)² = a² + b² + 2ab}

Now, open the brackets,   

= 49x² + 36y^{2 +} 84xy- 25x² – 4y² – 20xy

Now, add or subtract like terms,

=  49x² – 25x² + 36y² – 4y² +84xy – 20xy

= 24x² + 32y² + 64xy

Hence, (7x + 6y)² – (5x + 2y)² = 24x² + 32y² + 64xy

Задача 6: Найдите решение для: (48 ÷ 3) – (6 × 7) – (12 × 5).

Решение:

Given,

(48 ÷ 3) – (6 × 7) – (12 × 5)

By solving the bracket at first, we get

= (16) – (42) – (60)

Now, open the brackets.

= 16 – 42 – 60

Now, add the positive and negative integers separately.

= 16 – 102

= -86

Therefore, (48 ÷ 3) – (6 × 7) – (12 × 5) = -86.