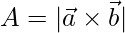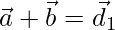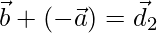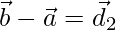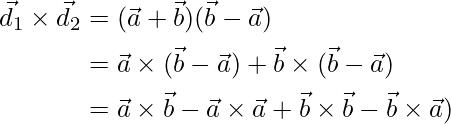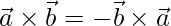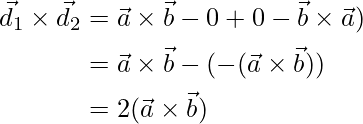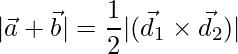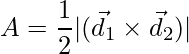Площадь параллелограмма

Площадь параллелограмма — это пространство или область, заключенная в двумерной фигуре в пределах ее четырех сторон. Параллелограмм в геометрии определяется как особый вид четырехугольника. Параллелограмм – это двумерная фигура, состоящая из четырех сторон. Противоположные стороны параллелограмма равны и параллельны друг другу. Площадь параллелограмма просто равна количеству квадратных единиц (например, м ² , см ² и т. д.), которые могут поместиться в параллелограмме.

Какова площадь параллелограмма?

The total surface occupies by the parallelogram on a two-dimensional plane surface is the area of a parallelogram. The area of a parallelogram can be determined by using its height, length of sides, or diagonals. All these three methods have their own derived formula that is explained below.

Формула площади параллелограмма

Площадь параллелограмма можно определить, умножив его основание на высоту. Как видно на следующей диаграмме, основание и высота параллелограмма перпендикулярны друг другу. Таким образом, для определения площади параллелограмма можно использовать следующую формулу:

Area of Parallelogram = Base × Height 

or 

A = b × h

where,

• b is the base of Parallelogram, and 
• h is the height of Parallelogram

Как рассчитать площадь параллелограмма?

Как правило, площадь параллелограмма можно вычислить, используя его основание и высоту. Кроме того, площадь параллелограмма также можно определить, если известны длины его параллельных сторон и любые углы между ними, а также углы, под которыми пересекаются две его диагонали. В результате есть три способа вычисления площади параллелограмма:

• Когда известны основание и высота параллелограмма.
• Когда известны длины сторон параллелограмма.
• Когда известны длины диагоналей параллелограмма.

Площадь параллелограмма через основание и высоту

Площадь параллелограмма с использованием высоты определяется произведением его основания и высоты.

Математически это записывается как

Area of parallelogram = b × h

where,

• b is the base of Parallelogram, and 
• h is the height of Parallelogram

Пример: Найдите площадь параллелограмма, если его основание 12 см, а высота 8 см.

Решение:

 Given that, 

 Base (b) = 12 cm

 Height (h) = 8 cm

The formula to calculate the area of a parallelogram is,

A = b × h 

= 12 × 8 

= 96 cm²

Площадь параллелограмма по длинам сторон

Площадь параллелограмма можно вычислить, используя длины сторон и смежных углов, если высота не задана.

Математически это записывается как,

Area of parallelogram = ab sin (θ)

where, 

• a and b are the lengths of parallel sides, and 
• θ is the angle between the sides.

Пример: если угол между двумя сторонами параллелограмма равен 30 градусов, а длины его смежных сторон равны 5 см и 6 см. Определить площадь параллелограмма.

Решение:

Given that, 

Length of one side (a) = 5 cm,

Length of the other side (b) = 4 cm,

Angle between the two adjacent sides (θ) = 30 degrees

The formula to calculate the area of a parallelogram is,

A = ab sin (θ)

= 5 × 4 × sin (30)

= 10 cm²

Площадь параллелограмма по диагоналям

Параллелограмм состоит из двух диагоналей, которые пересекаются друг с другом под определенным углом и встречаются в определенной точке. Площадь параллелограмма можно вычислить, используя длину его диагоналей.

Формула площади параллелограмма с использованием длины диагоналей:

Area of parallelogram = 1/2 × d₁ × d₂ sin (x)

where,

• d₁ and d₂ are the lengths of the diagonals and
• x is the angle between the diagonals.

Пример: Определить площадь параллелограмма, если угол между двумя пересекающимися диагоналями параллелограмма равен 90 градусов, а длины его смежных сторон равны 2 см и 6 см.

Решение:

Given that, 

Length of one diagonal (d₁) = 2 cm,

Length of the other diagonal (d₂) = 6 cm,

Angle between the two intersecting diagonals (x) = 90 degrees

The formula to calculate the area of a parallelogram is,

A = 1/2 × d₁ × d₂ sin (x)

= 1/2 × 2 × 6 × sin (90)

= 60 cm²

Площадь параллелограмма в векторной форме

Площадь параллелограмма можно вычислить, даже если стороны и диагонали параллелограмма заданы в векторной форме. Рассматривая параллелограмм PQRS со смежными сторонами а также 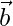соответственно. А диагонали есть 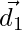а также 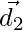, как показано ниже на диаграмме:

Now, the area of parallelogram in vector form is given by using the adjacent sides  and  as, 

From the above diagram of parallelogram, this can be interpreted as:

and 

or

Now, 

But, vec a imes vec a = 0, vec b imes vec b = 0 and 

Therefore, 

or

Thus from equation (1), the area of parallelogram in vector form is stated as:

Сводная информация о площади параллелограмма

• Area of a parallelogram using Base and Height:

A = b × h

• Area of a parallelogram using the side lengths:

A = ab sin (θ)

• Area of parallelogram using diagonals:

A = 1/2 × d₁ × d₂ sin (x)

Решенные примеры на основе площади параллелограмма

Пример 1: Найдите площадь параллелограмма, если его основание 10 см, а высота 8 см.

Решение:

Given:

Base (b) = 10 cm

Height (h) = 8 cm

We have,

A = b × h

= 10 × 8

= 80 cm²

Пример 2: Найдите площадь параллелограмма, основание которого равно 5 см, а высота 4 см.

Решение:

Given,

Base (b) = 5cm 

Height (h) = 4cm

Area(A) = b × h 

A = 5 × 4 

= 20 cm²

Пример 3: Определить площадь параллелограмма, если угол между двумя пересекающимися диагоналями параллелограмма равен 90 градусов, а длины его смежных сторон равны 4 см и 8 см.

Решение:

Given that, 

Length of one diagonal (d₁) = 4 cm,

Length of the other diagonal (d₂) = 8 cm,

Angle between the two intersecting diagonals (x) = 90 degrees

The formula to calculate the area of a parallelogram is,

A = 1/2 × d₁ × d₂ sin (x)

= 1/2 × 4 × 8 × sin (90)

= 16 cm²

Пример 4: Если угол между двумя сторонами параллелограмма равен 60 градусов, а длины его смежных сторон равны 3 см и 6 см. Определить площадь параллелограмма.

Решение:

Given that,

Length of one side (a) = 3 cm,

Length of the other side (b) = 6 cm,

Angle between the two adjacent sides (θ) = 60 degrees

The formula to calculate the area of a parallelogram is,

A = ab sin (θ)

= 3 × 6 × sin (60)

= 15.6 cm²

Пример 5: Найдите площадь параллелограмма, параллельные стороны которого равны 4 см и 3 см, а угол между этими сторонами равен 90°.

Решение:

Given,

Let the lengths of the sides by a and b with values 4 cm and 3 cm respectively.

Angle between the sides 90°

Area = ab sinθ

= 4 × 3 sin 90°

= 12 cm²

Часто задаваемые вопросы о площади параллелограмма

Вопрос 1: Что такое периметр параллелограмма?

Отвечать:

The Perimeter of a parallelogram is defined as the sum of its all four sides, so is given as,

Perimeter of a Parallelogram, P = 2 (a + b)

where a and b are the length of the opposite sides of a parallelogram. 

Вопрос 2: Почему площадь основания параллелограмма равна высоте?

Отвечать:

Since a parallelogram is a quadrilateral with two pairs of parallel sides. And perimeter is defined as the distance around a2-D figure. Therefore, the area of a parallelogram is equal to the base multiplied by the height.

Вопрос 3: Каковы свойства параллелограмма?

Отвечать:

The Properties of Parallelogram are:

• The opposite sides of a parallelogram are equal and parallel to each other.
• The opposite angles of a parallelogram are equal.
• The sum of interior angles of a parallelogram is equal to 360°.
• The adjacent angles of a parallelogram must be supplementary i.e. equal to 180°.

Вопрос 4: Все ли стороны параллелограмма равны?

Отвечать:

No, not all sides of a parallelogram are equal to each other. Only opposite sides of a parallelogram are equal.

Вопрос 5: Все ли углы параллелограмма равны?

Отвечать:

No, not all angles of a parallelogram are equal to each other. Only opposite angles of a parallelogram are equal.

Вопрос 6: По какой формуле находится высота параллелограмма?

Отвечать:

The formula for the height of a parallelogram, when the area and the base of a parallelogram are known then:

h = A/b

where,

• h is the height, 
• b is the base and
• A is the area of the parallelogram