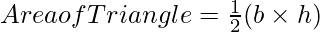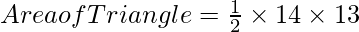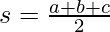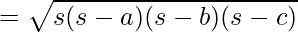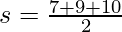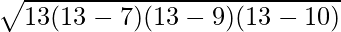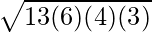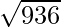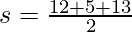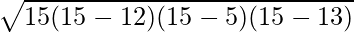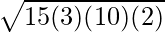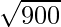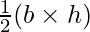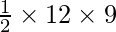Площадь 2D-форм

Площадь - это величина, которая выражает размер двухмерной фигуры или формы или плоской пластинки на плоскости. Формы пластин включают двумерные фигуры, которые можно нарисовать на плоскости, например круг, квадрат, треугольник, прямоугольник, трапецию, ромб и параллелограмм.

Многоугольник - это двухмерная фигура, образованная прямыми линиями. Примеры многоугольников - треугольники, шестиугольники и пятиугольники.

Имена фигур описывают, сколько сторон существует у фигуры. Например, треугольник состоит из трех сторон, а прямоугольник - из четырех. Следовательно, любая форма, которая может быть образована с использованием трех прямых линий, известна как треугольник, а любая форма, которую можно нарисовать, соединяя четыре линии, известна как четырехугольник.

Площадь - это область внутри границы / периметра фигур, которую необходимо учитывать.

Площадь 2D-форм

Площадь любой 2D-формы - это размер области, заключенной в нее. В геометрии площадь может быть определена как пространство, занимаемое плоскостью или поверхностью объекта. Площадь фигуры - это количество единичных квадратов, покрывающих поверхность фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.

SI unit: Square metre (m²)

Это некоторые двумерные геометрии

• Круг

• Прямоугольник

• Квадрат

• Треугольник и т. Д.

Круг

Круг - это замкнутая плоская геометрическая фигура. С технической точки зрения, круг - это геометрическое место точки, движущейся вокруг фиксированной точки на фиксированном расстоянии от точки. Круг - это форма, состоящая из всех точек на плоскости, которые находятся на заданном расстоянии от данной точки, центра. Это кривая, очерченная точкой, которая движется в плоскости так, что расстояние от нее до данной точки остается постоянным.

По сути, круг - это замкнутая кривая, внешняя линия которой находится на одинаковом расстоянии от центра. Фиксированное расстояние от точки - это радиус круга.

В реальной жизни вы получите множество примеров круга, таких как колесо, пицца, круглая площадка и т. Д.

Радиус

Радиус круга - это линия, соединяющая центр круга с внешней границей. Обычно обозначается буквой «r» или «R».

В формуле для площади и длины окружности радиус играет важную роль, о чем вы узнаете позже.

Диаметр

Диаметр круга - это линия, разделяющая круг на две равные части. Проще говоря, мы можем сказать, что это всего лишь удвоенный радиус круга и обозначается буквой d 'или' D '.

Следовательно, d = 2r или D = 2R

Если диаметр круга нам известен, мы можем вычислить радиус круга, например:

r = d / 2 или R = D / 2

или

Это кривая, очерченная точкой, которая движется в плоскости так, что расстояние от нее до данной точки остается постоянным.

Площадь круга

Любая геометрическая форма имеет свою площадь. Эта область представляет собой область, которую занимает фигура в двумерной плоскости. Таким образом, площадь, покрываемая одним полным циклом радиуса круга на двумерной плоскости, является площадью этого круга.

Как теперь вычислить площадь любого круглого объекта или пространства? В этом случае мы используем формулу площади круга.

В геометрии площадь, ограниченная кругом радиуса r, равна πr². Здесь греческая буква π представляет постоянное отношение длины окружности любого круга к его диаметру, примерно равное 22/7 или 3,14159.

Example: Find Out the area of the following circle.

Given:

Radius of Circle r= 7 cm

Find Out:

Area of Circle=?

Formula Used:

Area of Circle= πr²

Putting the value of r in formula

Area of Circle = 3.14159 × 7 × 7

Area of Circle=154 cm²

Прямоугольник

Площадь прямоугольника - это область, охватываемая прямоугольником в двухмерной плоскости. Прямоугольник - это двумерная фигура с четырьмя сторонами и четырьмя вершинами. Все четыре угла прямоугольника - прямые. Противоположные стороны прямоугольника равны и параллельны друг другу.

Следует отметить, что противоположные стороны параллелограмма также равны и параллельны друг другу, но углы не равны 90 градусам. Его также можно определить как: равносторонний четырехугольник, поскольку равноугольный означает, что все его углы равны; или параллелограмм, содержащий прямой угол.

Размер любого объекта можно измерить разными способами. Например, мы все обычно рассчитываем высоту здания или размер бассейна и его глубину.

Какая площадь прямоугольного объекта, как узнать площадь прямоугольника? Боковые и общие площади поверхности можно рассчитать только для трехмерных фигур. Мы не можем рассчитать прямоугольник, так как это двухмерная фигура.

Прямоугольник

Площадь прямоугольника

Площадь прямоугольника равна произведению длины и высоты прямоугольника.

Площадь прямоугольника ABCD = h × l

Example: Find Out the area of the following rectangle

Given:

Length of Rectangle l = 16 cm

Height of Rectangle h = 11 cm

Find Out:

Area of Rectangle =?

Formula Used:

Area of Rectangle = h × l

Putting the value of h and l in formula

Area of Rectangle = 11 × 16

Area of Rectangle =176 cm²

Квадрат

Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения квадрата. В общем, область определяется как область, занимаемая внутри границы плоского объекта или двухмерной фигуры. Измерения производятся в квадратных единицах, стандартной единицей измерения являются квадратные метры (м ² ).

Квадрат - это четырехсторонний многоугольник (форма 2d), четыре стороны которого равны по длине, а все углы равны 90 °.

или

Квадрат - это прямоугольник со всеми равными сторонами. Площадь - это пространство, покрытое объектом. Это область, занятая любой формой.

При измерении площади квадрата мы учитываем только длину его стороны. Все стороны квадрата равны, следовательно, его площадь равна квадрату стороны.

Квадрат

Площадь Квадрата

Площадь Квадрата равна квадрату стороны Квадрата.

Площадь квадрата = (сторона) ²

Площадь квадрата = ²

Example: Find Out the area of the following square.

Given:

Side of Rectangle a = 8 cm

Find Out:

Area of Square =?

Formula Used:

Area of Square = a²

Putting the value of h and l in formula

Area of Rectangle = (8cm)²

Area of Rectangle = 64 cm²

Треугольник

Треугольник - это многоугольник с тремя ребрами и тремя вершинами. Это одна из основных геометрических фигур. В общем, термин «область» определяется как область, занимаемая внутри границы плоского объекта или фигуры. Измерения производятся в квадратных единицах, стандартной единицей измерения являются квадратные метры (м2).

Для вычисления площади существуют заранее определенные формулы для квадратов, прямоугольников, круга, треугольников и т. Д. Площадь треугольника определяется как общая область, которая заключена между тремя сторонами любого конкретного треугольника. Он применим ко всем типам треугольников, будь то разносторонние, равнобедренные или равносторонние. Следует отметить, что основание и высота треугольника перпендикулярны друг другу.

Треугольник с вершинами A, B и C обозначается треугольником ABC.

Или

В евклидовой геометрии любые три точки, когда они не коллинеарны, определяют уникальный треугольник и одновременно уникальную плоскость.

Треугольник

Площадь Треугольника

Для данного треугольника, где основание треугольника - b, а высота - h, площадь треугольника может быть вычислена по формуле, например:

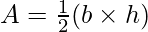
Мы также можем определить площадь треугольника с помощью формулы Герона, если высота h неизвестна. Итак, теперь мы обсудим формулу цапли.

Example: Find out the area of the triangle with height of 13 cm and base of 14 cm.

Given:

Base of Triangle b = 14 cm

Height of Triangle h = 13 cm

Find out: Area of Triangle =?

Formula Used:

Putting the value of h and l in formula

Area of Triangle = 91 cm²

Формула Герона

Его также называют формулой героя. Нам не нужно знать угол треугольника, чтобы вычислить его площадь. В геометрии формула Герона (иногда называемая формулой Героя), названная в честь Героя Александрийского, дает площадь треугольника, когда известны длины всех трех сторон.

Герой Александрии был великим математиком, который вывел формулу для вычисления площади треугольника, используя длину всех трех сторон. Он также расширил эту идею, чтобы найти площадь четырехугольника, а также многоугольников более высокого порядка.

Эта формула находит широкое применение в тригонометрии, например при доказательстве закона косинусов, закона котангенсов и т. Д.

Согласно Герону, мы можем найти площадь любого заданного треугольника, будь то разносторонний, равнобедренный или равносторонний, используя формулу с учетом сторон треугольника.

Предположим, треугольник ABC, стороны которого равны a, b и c соответственно. Таким образом, площадь треугольника можно определить как;

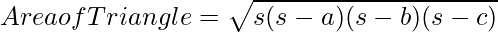
Where

a = length of side a

b = length of side b

c = length of side c

s = semi-perimeter

Пример: узнать площадь следующего треугольника

Given:

First side of Triangle a = 7 cm

Second side of Triangle b = 9 cm

Third side of Triangle c = 10 cm

Find Out:

Area of Triangle =?

Formula Used:

Area of Triangle 

Putting the values in formula

s = 13

Now

Area of Triangle = 

Area of Triangle = 

Area of Triangle = 

Area of Triangle = 30.59 cm²

Применение формулы Герона для определения площади четырехугольника

Четырехугольник можно нарисовать как сумму двух треугольников, поэтому мы можем использовать формулу Герона для определения площади четырехугольника. Мы можем понять это на примере

Пример: найдите площадь следующего четырехугольника с помощью формулы Герона.

Given:

Length of quadrilateral l = 12 cm

Height of quadrilateral h = 5 cm

Find Out:

Area of quadrilateral =?

Formula Used:

Area of quadrilateral using Heron’s Formula.

Quadrilateral ABCD can also be draw as sum of two triangles ABD and BCD

We can calculate area of triangles using heron’s Formula where

a = 12 cm

b = 5 cm

c = 13 cm (Using Pythagoras Theorem)

Now area of triangle ABD

s = 15

Now

Area of Triangle = 

Area of Triangle = 

Area of Triangle = 

Area of Triangle = 30 cm²

Similarly, area of triangle BCD = 30 cm²

Total Area of ABCD = Area of triangle ABD + Area of triangle BCD

Area of ABCD = 30 cm² + 30 cm²

Area of ABCD = 60 cm²

We can verify this answer using simple area formula of rectangle which is length × height. Area of rectangle is 12×5 equals to 60 cm² which is equal using Heron’s Formula.

Пример: Найдите площадь треугольника высотой 12 см и основанием 9 см.

Решение:

Given:

Base of Triangle b = 9 cm

Height of Triangle h = 12 cm

Find out: Area of Triangle =?

Formula Used:

Area of Triangle = 

Putting the value of h and l in formula

Area of Triangle = 

Area of Triangle = 54cm²