Остающийся элемент после выполнения альтернативных операций побитового ИЛИ и побитового исключающего ИЛИ над соседними парами

Опубликовано: 17 Января, 2022

Дан массив из N (всегда степень двойки) элементов и Q запросов.
Каждый запрос состоит из двух элементов, индекса и значения ... Нам нужно написать программу, которая присваивает значение индексу A и печатает единственный элемент, который остается после выполнения следующих операций для каждого запроса:

  • На альтернативных шагах выполните операции побитового ИЛИ и побитового исключающего ИЛИ над соседними элементами.
  • На первой итерации выберите, выберите n / 2 пар, перемещающихся слева направо, и выполните побитовое ИЛИ для всех значений пар. На второй итерации выберите (n / 2) / 2 оставшихся пары и выполните поразрядную операцию XOR. На третьей итерации выберите, выберите ((n / 2) / 2) / 2 оставшиеся пары, двигаясь слева направо, и выполните побитовое ИЛИ для всех значений пары.
  • Продолжайте описанные выше шаги, пока не останется единственный элемент.

Примеры:

 Ввод: n = 4 m = 2 
        arr = [1, 4, 5, 6] 
        Запросы- 
        1-й: индекс = 0 значение = 2  
        2-й: индекс = 3 значение = 5
Выход: 1 
         3 
Пояснение : 

1-й запрос:
Присваивая 2 индексу 0, последовательность теперь 
[2, 4, 5, 6]. 
1-я итерация: есть 4/2 = 2 пары (2, 4) и (5, 6) 
2 ИЛИ 4 дает 6, а 5 ИЛИ 6 дает 7. Таким образом, 
последовательность теперь [6, 7]. 

2-я итерация: осталась 1 пара (6, 7) 
6 ^ 7 = 1. 

Следовательно, последний оставшийся элемент равен 1, что является 
ответ на наш первый вопрос. 

2-й запрос:
Присвоив 5 к индексу 3, последовательность теперь 
[2, 4, 5, 5]. 
1-я итерация: есть 4/2 = 2 пары (2, 4) и (5, 5) 
2 ИЛИ 4 дает 6, а 5 ИЛИ 5 дает 5. Таким образом, 
последовательность теперь [6, 5]. 

2-я итерация: осталась 1 пара (6, 5) 
6 ^ 5 = 3. 

Следовательно, последний оставшийся элемент равен 3, что является
ответ на наш второй вопрос.
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Наивный подход : наивный подход состоит в том, чтобы выполнять каждый шаг, пока не останется один элемент. Используя двумерный вектор, мы будем хранить результирующие элементы, оставшиеся после каждого шага. V [steps-1] [0..size] дает количество элементов на предыдущем шаге. Если номер шага нечетный, выполняется побитовая операция ИЛИ, в противном случае выполняется побитовая операция исключающее ИЛИ. Повторяйте шаги, пока у нас не останется остаток с одним элементом. Последний оставшийся элемент будет нашим ответом.

Below is the implementation of the naive approach: 

C++

// CPP program to print the Leftover element after
// performing alternate Bitwise OR and Bitwise XOR
// operations to the pairs.
#include <bits/stdc++.h>
using namespace std;
#define N 1000
 
int lastElement(int a[],int n)
{
    // count the step number
    int steps = 1;
    vector<int>v[N];
 
    // if one element is there, it will be the answer
    if (n==1) return a[0];
 
 
    // at first step we do a bitwise OR
    for (int i = 0 ; i < n ; i += 2)
        v[steps].push_back(a[i] | a[i+1]);
 
 
    // keep on doing bitwise operations till the
    // last element is left
    while (v[steps].size()>1)
    {
 
        steps += 1;
 
        // perform operations
        for (int i = 0 ; i < v[steps-1].size(); i+=2)
        {
            // if step is the odd step
            if (steps&1)
                v[steps].push_back(v[steps-1][i] | v[steps-1][i+1]);
            else  // even step
                v[steps].push_back(v[steps-1][i] ^ v[steps-1][i+1]);
        }
    }
 
    // answer when one element is left
    return v[steps][0];
}
 
// Driver Code
int main()
{
    int a[] = {1, 4, 5, 6};
    int n = sizeof(a)/sizeof(a[0]);
 
    // 1st query
    int index = 0;
    int value = 2;
    a[0] = 2;
    cout << lastElement(a,n) << endl;
 
    // 2nd query
    index = 3;
    value = 5;
    a[index] = value;
    cout << lastElement(a,n)  << endl;
 
    return 0;
}

Java

// Java program to print the Leftover element
// after performing alternate Bitwise OR and
// Bitwise XOR operations to the pairs.
import java.util.*;
 
class GFG
{
static int N = 1000;
 
static int lastElement(int a[], int n)
{
    // count the step number
    int steps = 1;
    Vector<Integer> []v = new Vector[N];
    for (int i = 0; i < N; i++)
        v[i] = new Vector<Integer>();
 
    // if one element is there,
    // it will be the answer
    if (n == 1) return a[0];
 
    // at first step we do a bitwise OR
    for (int i = 0 ; i < n ; i += 2)
        v[steps].add(a[i] | a[i + 1]);
 
    // keep on doing bitwise operations
    // till the last element is left
    while (v[steps].size() > 1)
    {
 
        steps += 1;
 
        // perform operations
        for (int i = 0; i < v[steps - 1].size(); i += 2)
        {
            // if step is the odd step
            if (steps % 2 == 1)
                v[steps].add(v[steps - 1].get(i) |
                             v[steps - 1].get(i + 1));
            else // even step
                v[steps].add(v[steps - 1].get(i) ^
                             v[steps - 1].get(i + 1));
        }
    }
 
    // answer when one element is left
    return v[steps].get(0);
}
 
// Driver Code
public static void main(String[] args)
{
    int a[] = {1, 4, 5, 6};
    int n = a.length;
 
    // 1st query
    int index = 0;
    int value = 2;
    a[0] = 2;
    System.out.println(lastElement(a, n));
 
    // 2nd query
    index = 3;
    value = 5;
    a[index] = value;
    System.out.println(lastElement(a, n));
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 program to print the Leftover element
# after performing alternate Bitwise OR and
# Bitwise XOR operations to the pairs.
N = 1000
 
def lastElement(a, n):
  
    # count the step number
    steps = 1
    v = [[] for i in range(n)]
 
    # if one element is there, it will be the answer
    if n == 1: return a[0]
 
    # at first step we do a bitwise OR
    for i in range(0, n, 2):
        v[steps].append(a[i] | a[i+1])
 
    # keep on doing bitwise operations
    # till the last element is left
    while len(v[steps]) > 1:
     
        steps += 1
        # perform operations
        for i in range(0, len(v[steps-1]), 2):
          
            # if step is the odd step
            if steps & 1:
                v[steps].append(v[steps-1][i] | v[steps-1][i+1])
            else: # even step
                v[steps].append(v[steps-1][i] ^ v[steps-1][i+1])
          
    # answer when one element is left
    return v[steps][0]
 
# Driver Code
if __name__ == "__main__":
  
    a = [1, 4, 5, 6]
    n = len(a)
 
    # 1st query
    index, value, a[0] = 0, 2, 2
    print(lastElement(a,n))
 
    # 2nd query
    index, value = 3, 5
    value = 5
    a[index] = value
    print(lastElement(a,n))
  
# This code is contributed by Rituraj Jain

C#

// C# program to print the Leftover element
// after performing alternate Bitwise OR and
// Bitwise XOR operations to the pairs.
using System;
using System.Collections.Generic;
 
class GFG
{
static int N = 1000;
 
static int lastElement(int []a, int n)
{
    // count the step number
    int steps = 1;
    List<int> []v = new List<int>[N];
    for (int i = 0; i < N; i++)
        v[i] = new List<int>();
 
    // if one element is there,
    // it will be the answer
    if (n == 1)
        return a[0];
 
    // at first step we do a bitwise OR
    for (int i = 0 ; i < n ; i += 2)
        v[steps].Add(a[i] | a[i + 1]);
 
    // keep on doing bitwise operations
    // till the last element is left
    while (v[steps].Count > 1)
    {
        steps += 1;
 
        // perform operations
        for (int i = 0; i < v[steps - 1].Count; i += 2)
        {
            // if step is the odd step
            if (steps % 2 == 1)
                v[steps].Add(v[steps - 1][i] |
                             v[steps - 1][i + 1]);
            else // even step
                v[steps].Add(v[steps - 1][i] ^
                             v[steps - 1][i + 1]);
        }
    }
 
    // answer when one element is left
    return v[steps][0];
}
 
// Driver Code
public static void Main(String[] args)
{
    int []a = {1, 4, 5, 6};
    int n = a.Length;
 
    // 1st query
    int index = 0;
    int value = 2;
    a[0] = 2;
    Console.WriteLine(lastElement(a, n));
 
    // 2nd query
    index = 3;
    value = 5;
    a[index] = value;
    Console.WriteLine(lastElement(a, n));
}
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
 
// Javascript program to print the Leftover element after
// performing alternate Bitwise OR and Bitwise XOR
// operations to the pairs.
var N = 1000
 
function lastElement(a,n)
{
    // count the step number
    var steps = 1;
    var v = Array.from(Array(N), ()=>Array(0));
 
    // if one element is there, it will be the answer
    if (n==1)
        return a[0];
 
 
    // at first step we do a bitwise OR
    for (var i = 0 ; i < n ; i += 2)
        v[steps].push(a[i] | a[i+1]);
 
 
    // keep on doing bitwise operations till the
    // last element is left
    while (v[steps].length>1)
    {
 
        steps += 1;
 
        // perform operations
        for (var i = 0 ; i < v[steps-1].length; i+=2)
        {
            // if step is the odd step
            if (steps&1)
                v[steps].push(v[steps-1][i] | v[steps-1][i+1]);
            else  // even step
                v[steps].push(v[steps-1][i] ^ v[steps-1][i+1]);
        }
    }
 
    // answer when one element is left
    return v[steps][0];
}
 
// Driver Code
var a = [1, 4, 5, 6];
var n = a.length;
// 1st query
var index = 0;
var value = 2;
a[0] = 2;
document.write( lastElement(a,n) + "<br>");
// 2nd query
index = 3;
value = 5;
a[index] = value;
document.write( lastElement(a,n));
 
</script>

Выход:

1
3

Сложность времени: O (N * 2 N )

Эффективный подход : эффективный подход - использовать дерево сегментов. Ниже приведено полное дерево сегментов, использованное для решения проблемы.

Строим дерево
Листья дерева сегментов будут хранить массив значений, а их родители сохранят ИЛИ листьев. Двигаясь вверх по дереву с каждым альтернативным шагом, родительский элемент сохраняет либо побитовое исключающее ИЛИ, либо побитовое ИЛИ между левым и правым дочерним элементом. На каждой итерации с нечетными номерами мы выполняем побитовое ИЛИ пар , и аналогичным образом мы выполняем побитовое исключающее ИЛИ пар при каждой операции с четными номерами . Таким образом, родительский элемент с нечетным номером будет хранить побитовое ИЛИ левого и правого дочерних элементов. Точно так же родительский элемент с четным номером хранит побитовое исключающее ИЛИ для левого и правого дочерних элементов. level [] - это массив, в котором хранятся уровни каждого родителя, начиная с 1, чтобы определить, выполняет ли пара (правый дочерний элемент и левый дочерний элемент) под ним операцию ИЛИ или операцию XOR. Корень дерева будет нашим ответом на заданную последовательность после каждой операции обновления.

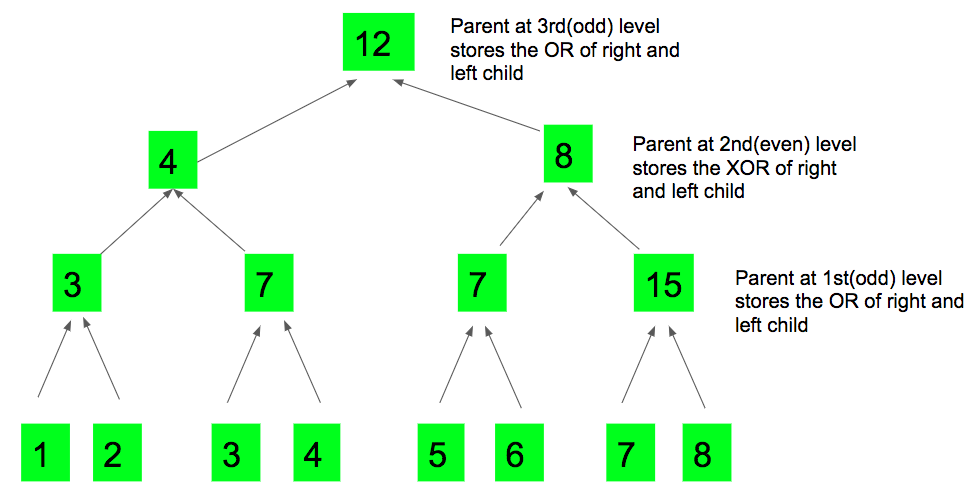
. На изображении выше поясняется конструкция дерева. Если последовательность была [1, 2, 3, 4, 5, 6, 7, 8], то после 3 итераций у нас останется 12, что является нашим ответом и сохраняется в корне.

Ответ на запрос
Нет необходимости перестраивать полное дерево для выполнения операции обновления. Чтобы выполнить обновление, мы должны найти путь от корня к соответствующему листу и пересчитать значения только для тех родителей, которые лежат на найденном пути.
Уровень родителя:
Используя DP на деревьях, мы можем легко сохранить уровень каждого родителя. Инициализируйте уровень конечных узлов до 0 и продолжайте добавлять по мере продвижения к каждому родительскому элементу.
Повторяющееся соотношение для вычисления уровня родителя:

level[parent] = level[child] + 1 
Here, a child is 2*pos + 1 or 2*pos + 2

Below is the implementation of the above approach: 

C++

// CPP program to print the Leftover element after
// performing alternate Bitwise OR and
// Bitwise XOR operations to the pairs.
#include <bits/stdc++.h>
using namespace std;
#define N 1000
 
// array to store the tree
int tree[N];
 
// array to store the level of every parent
int level[N];
 
// function to construct the tree
void constructTree(int low, int high, int pos, int a[])
{
    if (low == high)
    {
        // level of child is always 0
        level[pos] = 0;
        tree[pos] = a[high];
        return;
    }
    int mid = (low + high) / 2;
 
    // recursive call
    constructTree(low, mid, 2 * pos + 1, a);
    constructTree(mid + 1, high, 2 * pos + 2, a);
 
    // increase the level of every parent, which is
    // level of child + 1
    level[pos] = level[2 * pos + 1] + 1;
 
    // if the parent is at odd level, then do a
    // bitwise OR
    if (level[pos] & 1)
        tree[pos] = tree[2 * pos + 1] | tree[2 * pos + 2];
 
    // if the parent is at even level, then
    // do a bitwise XOR
Структуры данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Различия между структурой данных массива и словаря
21 Января, 2023
TCS SDE Sheet: Вопросы и ответы для интервью
12 Января, 2023
Множественные сравнения в очереди приоритетов С++?
6 Января, 2023
Когда использовать Queue over ArrayList в Java?
6 Января, 2023
Введение в связанный список — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Введение в массивы — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Как подготовиться к ICFP или Международной конференции по функциональному программированию?
12 Декабря, 2022