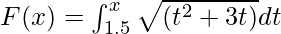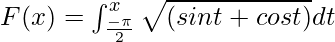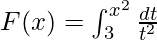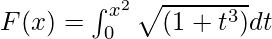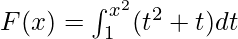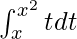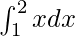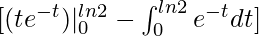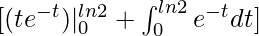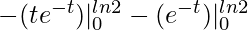Основная теорема исчисления

В математике исчисление — это ветвь, которая помогает понять изменения между значениями, которые связаны с функцией. Он широко используется в области физики, техники, медицины, экономики, биологии, освоения космоса, статистики, фармакологии и многих других областях. Без расчета даже дом не построить.

История исчисления восходит к Древнему Египту. Историки говорят, что метод, используемый египтянами для расчета объема усеченной пирамиды, был интегральным исчислением. Они знали об основных функциях интегрального исчисления и использовали их для вычисления объемов и площадей. Однако современное исчисление было разработано Исааком Ньютоном и Готфридом Вильгельмом Лейбницем независимо друг от друга.

Есть две ветви исчисления:

1. Дифференциальное исчисление: в этом разделе исчисления мы делим вещи на разные части и изучаем, как они меняются от одного момента к другому. Например, изменение скорости во времени.
2. Интегральное исчисление: в этом разделе исчисления мы соединяем маленькие кусочки вместе, чтобы понять их общее поведение. Например, при определении длины силового кабеля, необходимого для соединения двух подстанций.

В этой статье мы обсудим фундаментальную теорему исчисления, которая объединяет две ветви исчисления, но перед этим нам сначала нужно понять функцию площади.

Площадь Функция

Рассмотрим функцию f(t) , непрерывную на интервале [a, b], как показано на изображении ниже:

Теперь отметим на графике некоторую точку x между a и b.

Теперь мы должны найти площадь под кривой y = f(t) между интервалом [a, x] .

Итак, площадь под кривой между а и х есть определенный интеграл от а до х от f(t) dt, равна

A(x) = ∫_a^x f(t) dt

Здесь A (x) известна как функция площади, и она помогает найти основную теорему исчисления. Или, другими словами, A(x), т. е. ∫ _a ^x f(t) dt — это площадь области, ограниченной кривой y = f(t) на оси t с координатами a и b. Если x является точкой между интервалом [a, b], то ∫ _a ^x f(t) dt будет представлять площадь заштрихованной области, которая равна A(x).

Пример:

Let’s find out the value of A(x) for function y = 2x between x = 2 and x = 6.

A(x) = ∫₂⁶ 2x dx = [x²]₂⁶ = 6² – 2² = 36 – 4 = 32 

Основная теорема исчисления

Основная теорема исчисления — мощная теорема математики. Он установил связь между дифференциацией и интеграцией. Теперь это соотношение дает нам метод оценки определенных внутренних без вычисления площадей или использования сумм Римана. Основная теорема делится на две части:

1. Первая фундаментальная теорема
2. Вторая фундаментальная теорема

Теперь мы подробно обсудим каждую теорему одну за другой:

Первая основная теорема

Первая фундаментальная теорема утверждает, что если f(x) — непрерывная функция на отрезке [a, b] и функция F(x) определяется равенством

dF/dx = d/dx(∫_a^x f(t) dt) = f(x)

Или F'(x) = f(x) над [a, b]

Или, другими словами, если f — непрерывная функция на отрезке [a, b], а функция площади — A(x), то

A"(x) = f(x) ∀ x ∈ [a, b]

Доказательство:

According to the fundamental theorem of calculus, we have

F"(x) = ∫_a^x f(t) dt = f(x)           …(A)

Now, the equation (A) can be written as

F"(x) = lim _h⇢0 (F(x + h) – F(x)/h

= lim _h⇢0 1/h [( ∫_a^x+h f(t) dt – ∫_a^x f(t) dt )]       …(B)

Thus, equation (B) represents the area under the curve y = f(t) on the 

interval [x, x + h]. Now, equation (B) can be written as

F"(x) = lim _h⇢0 1/h (∫_x^x+h f(t) dt         …(C)

Now, according to the mean value theorem of the definite integral,

if there exists a c such that x ≤ c ≤ x + h then

f(c) = 1/h ∫_x^x+h f(t) dt

Thus,

F"(x) = lim _h⇢0 f(c)

Since c is in between x and x + h, therefore c⇢x as h⇢0. 

Also, since f(x) is continuous, therefore we have,

lim _h⇢0 f(c) = lim _c⇢x f(c) = f(x)

Thus,

F"(x) = lim _h⇢0 1/h ∫_x^x+h f(t) dt

= lim _h⇢0 f(c)

= f(x)

Hence, proved.

Примечание:

• Каждая непрерывная функция f имеет первообразную F(x).
• Основная теорема исчисления связывает интегральное исчисление и дифференциальное исчисление.

Нахождение производной с помощью основной теоремы исчисления:

Давайте обсудим эту концепцию с помощью примера:

Let’s say we have a function F(x) = ∫₂₁^x √(t³) dt and we have to find F"(4).

So, according to the fundamental theorem of calculus, the given equation becomes

 F"(x) = √(x³)

Thus, F"(4) = √(4³) = 4^3/2 = (4^1/2)³ = (√4)³ = 2³ = 8.

This is how we solve questions when we have to apply the fundamental theorem of calculus.

Нахождение производной с помощью основной теоремы исчисления: x находится на обеих границах:

Давайте обсудим эту концепцию с помощью примера:

Suppose there’s a function y = f(t) = sin t/t which is continuous in [x, x²] and we have to find it’s antiderivative. Let’s consider the following diagram :

According to the fundamental theorem of calculus,

   …..(1)

Now, mark c on the graph somewhere in between x and x² on the graph.

Now, equation (1) becomes

dF/dx = d/dx ( ∫_x^c sin t/t dt ) + d/dx ()

= – d/dx ( ∫_c^x sin t/t dt ) + d/dx ()

= – sin x/x + (sin x²/x²).2x

= (2 sin x² – sin x)/x

Thus, we get

F"(x) = (2 sin x² – sin x)/x

Hence, this is how we find derivatives of the functions where x is on both bounds.

Вторая фундаментальная теорема исчисления

Вторая фундаментальная теорема исчисления утверждает, что если f(x) непрерывна на отрезке [a, b] и F(x) является первообразной f(x), то

∫_a^b f(x) dx = F(b) – F(a)

Вторая фундаментальная теорема также известна как теорема об оценке.

• Эта теорема утверждает, что ∫ _a ^b f(x) dx = значение первообразной F от «f» на верхнем пределе b – то же самое значение первообразной на нижнем пределе a.
• В выражении ∫ _a ^b f(x) dx функция f(x) должна быть корректно определена и непрерывна на интервале [a, b].
• Это очень полезная теорема. Он обеспечивает метод оценки определенного интеграла без нахождения предела суммы.
• Здесь при оценке определенного интеграла основной операцией является нахождение функции, производной которой является уравнение для интегрирования, и этот процесс усилит связь дифференцирования и интегрирования.

Доказательство:

Let us consider M = x_i, i = 0, 1, …, n is a regular partition of [a, b]

Then 

F(b) – F(a) = F(x_n) – F(x₀)

= [F(x_i) – F(x_{i – 1})]   …..(1)

Now, As we know that F is the antiderivative of f on the closed interval [a, b], 

So using the mean value theorem, we get

i = 0, 1, 2, …,n

Now we find the value of c_i in [x_i-1, x_i]

So, 

F(x_i) – F(x_{i – 1}) = F"(c_i)(x_i – x_i-1) = f(c_i)△x

Now put this value in equation(1), we get

F(b) – F(a) =  f(c_i)△x

Now taking limit on both sides, i.e., n -> ∞, we get

F(b) – F(a) = lim_n->∞ f(c_i)△x = ∫^b_a f(x)dx

Hence proved

Примеры проблем

Вопрос 1. Вычислить производную функции при х = 3.

Решение:

Given that 

So, using first FTC, we get

F"(x) =  = √(x² + 3x)

Therefore,

F"(3) = √(3² + 3.3) = √(9 + 9) = √(2.9) = 3√2.

Вопрос 2. Вычислить производную функции 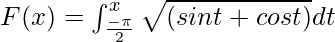dt при x = π /2.

Решение:

Given that 

So, using first FTC, we get

F"(x) =  = f(x)

Hence,

F"(x) = √(sin x + cos x)

Therefore,

F"(π/2) = √(sin π/2 + cos π/2) = √(1 + 0) = 1.

Вопрос 3. Найдите производную от .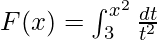

Решение:

Given that 

So, let x² = u. 

Now, consider a new function,

G(u) = ∫₃^u dt/t² 

⇒ G"(u) = 1/u²

Since, F(x) = G(x²)

⇒ F"(x) = G"(x²).2x

⇒ F"(x) = (1/x⁴).2x

⇒ F"(x) = 2/x³.

Вопрос 4. Найдите производную от .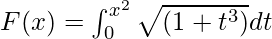

Решение:

Given that 

So, let x² = u. 

Now, consider a new function,

G(u) = ∫₀^u √(1 + t³) dt

Using first FTC, we have

G"(u) = √(1 + u³)

As F(x) = G(x²)

⇒ F"(x) = G"(x²).2x

⇒ F"(x) = 2x √(1 + (x²)³)

⇒ F"(x) = 2x √(1 + x⁶).

Вопрос 5. Найдите производную функции .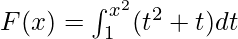

Решение:

Given that 

So, let x² = u. 

Now, considering new function,

G(u) =  ∫₁^u (t² + t) dt.

Using first FTC, we get

G"(u) = u² + u

Since, F(x) = G(x²)

⇒ F"(x) = G"(x²).2x

⇒ F"(x) = (x⁴ + x).2x

⇒ F"(x) = 2x⁵ + 2x².

Вопрос 6. Вычислить интеграл .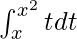

Решение:

Given that 

Now we find the anti-derivative of t

∫t dt = t² + C

Now using the second FTC, we get

∫_a^b f(x) dx = F(b) – F(a)

 = F(x²) – F(x)

 = ((t²)²) – (t²)

 = (t⁴) – (t²)

 = t²((t²) – 1)

Вопрос 7. Вычислите интеграл .

Решение:

Given that I = 

Now using the second FTC, we get

∫_a^b f(x) dx = F(b) – F(a)

 = F(2) – F(1)

Now we find the anti-derivative of x

∫x dx = x² + C

 = (2²) – 1

= 4 – 1

= 3

Вопрос 8. Вычислите интеграл ∫ ₀ ² (x ² – x) dx.

Решение:

Given I = ∫₀² (x² – x) dx

Using second FTC, we get

∫_a^b f(x) dx = F(b) – F(a)

∫₀² (x² – x) dx = F(2) – F(0)

Now we find the anti-derivative of x

∫₀² (x² – x) dx = x³/3 – x²/2

So, 

= [x³/3 – x²/2]₀²

= [8/3 – 4/2]

= [8/3 – 2]

= [8/3 – 6/3]

= 2/3.

Вопрос 9. Вычислить интеграл F(x) = ∫ ₀ ^x e ^t + e ^-t dt.

Решение:

Given that F(x) = ∫₀^x e^t + e^-t dt

Using the first FTC, we get

F"(x) = e^x + e^-x.

Вопрос 10. Найдите интеграл от .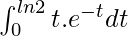

Решение:

Given I = 

so we can also write as

I = 

Now apply integration by parts, we get

u = t, dv = d(e^-t)

So, du = 1, v = e^-t

So, the integral is

I = –

=

= 

=

= 

= -e^-ln2(ln2 + 1) + e⁰ .1

= 1/2(ln e – ln 2)

= 1/2ln e/2