Ogive (кумулятивная кривая частоты) и ее типы
Метод представления данных в виде графиков, который обеспечивает быстрый и простой способ понять тенденции данного набора данных, известен как графическое представление. Заданный набор данных может быть представлен в виде диаграммы; однако со статистической точки зрения исследователи предпочитают графическое представление, поскольку оно обеспечивает более точное и уместное представление данных. Графическое представление данных облегчает процесс сравнения двух или более ситуаций. Два типа графиков, посредством которых данный набор данных может быть представлен, — это Графики частотного распределения и Графики временных рядов .
Четыре наиболее распространенных графика в разделе «График распределения частот» — это график линейной частоты, гистограмма, многоугольник частоты, кривая частоты и ожив.
боеголовка
Ogive или кумулятивная кривая частоты - это кривая набора данных, полученного человеком посредством представления кумулятивного частотного распределения на графике. Поскольку существует два типа кумулятивного частотного распределения; т.е. Меньше, чем кумулятивные частоты и Больше, чем кумулятивные частоты, оживы также бывают двух типов:
1. Меньше, чем ожив
2. Больше, чем Огив
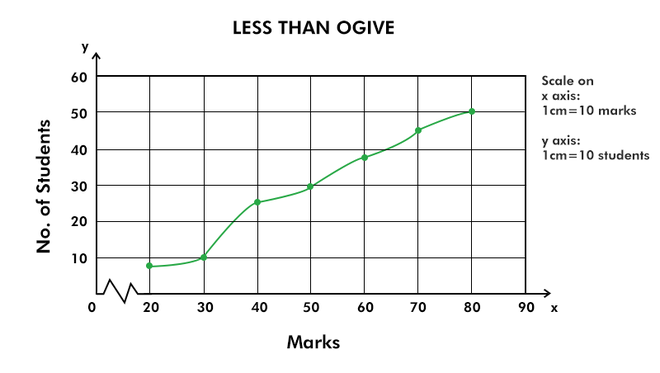
Меньше, чем Ожив
Шаги, необходимые для представления графа меньше, чем ожив, следующие:
Шаг 1
Чтобы представить менее оживальный график, добавьте частоты всех предыдущих интервалов класса к частоте класса.
Шаг 2
После этого по оси Y отобразите менее кумулятивных частот по отношению к верхнему пределу соответствующего интервала класса по оси X.
Шаг 3
На последнем шаге соедините эти точки плавной кривой от руки, которая в результате будет меньше, чем оживальная.
Кривая меньше, чем оживальная, представляет собой возрастающую кривую, которая имеет наклон вверх слева направо.
Example:
Draw a ‘less than’ ogive curve from the following distribution of the marks of 50 students in a class.
Marks 10-20
20-30
30-40
40-50
50-60
60-70
70-80
No. of Students 6
4
15
5
8
7
5
Solution:
First of all, we have to convert the frequency distribution into a less than cumulative frequency distribution.
Marks
No. of Students (f)
No. of Students (cf)
Less than 20
6
6
Less than 30
4
6 + 4 = 10
Less than 40
15
6 + 4 + 15 = 25
Less than 50
5
6 + 4+ 15 + 5 = 30
Less than 60
8
6 + 4 + 15 + 5 + 8 = 38
Less than 70
7
6 + 4 + 15 + 5 + 8 + 7 = 45
Less than 80
5
6 + 4 + 15 + 5 + 8 + 7 + 5 = 50
Now, plot these values of cumulative frequency on a graph.
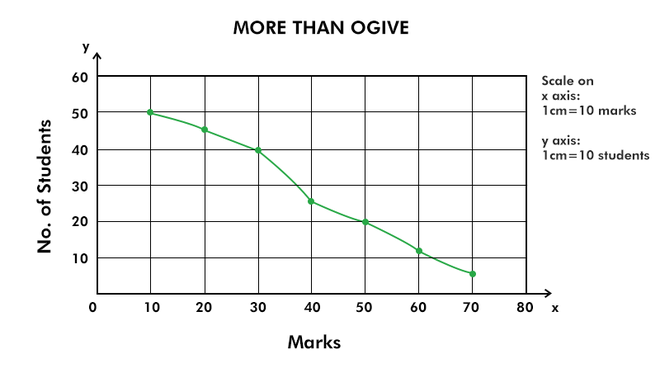
Больше, чем Огив
Шаги, необходимые для представления более чем оживального графика, следующие:
Шаг 1
Чтобы представить более чем живой график, добавьте частоты всех последующих интервалов класса к частоте класса.
Шаг 2
После этого отложите по оси Y более чем совокупные частоты в сравнении с верхним пределом соответствующего интервала класса по оси X.
Шаг 3
На последнем шаге соедините эти точки плавной кривой от руки, что в результате даст больше, чем ожив.
Более чем оживальная кривая представляет собой убывающую кривую, которая наклонена вниз слева направо.
Example:
Draw a ‘more than’ ogive curve from the following distribution of the marks of 50 students in a class.
Marks 10-20
20-30
30-40
40-50
50-60
60-70
70-80
No. of Students 6
4
15
5
8
7
5
Solution:
First of all, we have to convert the frequency distribution into a more than cumulative frequency distribution.
Marks
No. of Students (f)
No. of Students (cf)
More than 10
6
5 + 7 + 8 + 5 + 15 + 4 + 6 = 50
More than 20
4
5 + 7 + 8 + 5 + 15 + 4 = 45
More than 30
15
5 + 7 + 8 + 5 + 15 = 40
More than 40
5
5 + 7 + 8 + 5 = 25
More than 50
8
5 + 7 + 8 = 20
More than 60
7
5 + 7 = 12
More than 70
5
5
Now, plot these values of cumulative frequency on a graph.
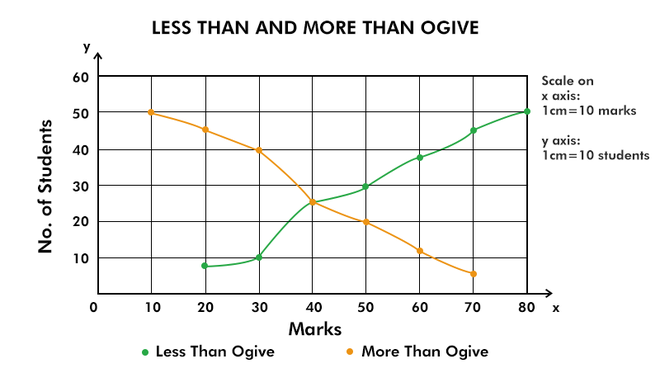
И «Меньше, чем», и «Больше, чем» Огивы
Оживы «меньше чем» и «больше чем» могут быть нанесены на один и тот же график, и точка, в которой эти две кривые пересекаются, является медианой данного набора данных.
Example:
Draw both ‘less than’ and ‘more than’ ogive curve from the following distribution of the marks of 50 students in a class.
Marks 10-20
20-30
30-40
40-50
50-60
60-70
70-80
No. of Students 6
4
15
5
8
7
5
Solution:
First of all, we have to convert the frequency distribution into a less than and more than cumulative frequency distribution.
Marks
No. of Students (cf)
Marks
No. of Students (cf)
Less than 20
6
More than 10
50
Less than 30
10
More than 20
45
Less than 40
25
More than 30
40
Less than 50
30
More than 40
25
Less than 60
38
More than 50
20
Less than 70
45
More than 60
12
Less than 80
50
More than 70
5
Now, plot these values of less than and more than cumulative frequency on a graph.