Обход дерева (Inorder, Preorder и Postorder)

Опубликовано: 5 Января, 2022

В отличие от линейных структур данных (массив, связанный список, очереди, стеки и т. Д.), Которые имеют только один логический способ обхода, деревья можно обходить по-разному. Ниже приведены обычно используемые способы обхода деревьев.

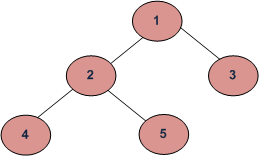
Обходы в глубину:
(а) Порядок (слева, корень, справа): 4 2 5 1 3
(б) Предварительный заказ (корень, слева, справа): 1 2 4 5 3
(c) Поступорядочение (слева, справа, корень): 4 5 2 3 1
Обход первого порядка ширины или уровня: 1 2 3 4 5
Пожалуйста, смотрите этот пост для первого обхода в ширину.
Inorder Traversal ( практика ):

 Алгоритм Inorder (дерево)
   1. Пройдите по левому поддереву, т. Е. Вызовите Inorder (left-subtree)
   2. Зайдите в рут.
   3. Пройдите по правому поддереву, т. Е. Вызовите Inorder (правое поддерево)

Использование Inorder
В случае двоичных деревьев поиска (BST) обход в порядке неубывания дает узлы в неубывающем порядке. Чтобы получить узлы BST в невозрастающем порядке, можно использовать вариант Inorder traversal, где Inorder traversal отменен.
Пример: обход указанного выше рисунка равен 4 2 5 1 3.
Обход предзаказа ( практика ):

 Предварительный заказ алгоритма (дерево)
   1. Зайдите в рут.
   2. Пройдите по левому поддереву, т. Е. Вызовите Preorder (left-subtree).
   3. Пройдите по правому поддереву, т. Е. Вызовите Preorder (правое поддерево).

Использование предзаказа
Предварительный обход используется для создания копии дерева. Предварительный обход также используется для получения префиксного выражения дерева выражения. Пожалуйста, посетите http://en.wikipedia.org/wiki/Polish_notation, чтобы узнать, почему префиксные выражения полезны.
Пример: обход предварительного заказа для указанной выше цифры составляет 1 2 4 5 3.
Пост порядковый обход ( практика ):

Algorithm Postorder(tree)
   1. Traverse the left subtree, i.e., call Postorder(left-subtree)
   2. Traverse the right subtree, i.e., call Postorder(right-subtree)
   3. Visit the root.

Использование Postorder
Поступорядоченный обход используется для удаления дерева. См. Подробности в вопросе об удалении дерева. Поступорядоченный обход также полезен для получения постфиксного выражения дерева выражений. См. Http://en.wikipedia.org/wiki/Reverse_Polish_notation для использования постфиксного выражения.
Пример: обратный ход для приведенного выше рисунка равен 4 5 2 3 1.

C ++

 // C++ program for different tree traversals
 #include <iostream>
 using namespace std;
 /* A binary tree node has data, pointer to left child
 and a pointer to right child */
 struct Node {
    data; int
    struct Node *left, *right;
    Node( data) int
    {
        this ->data = data;
        left = right = NULL;
    }
 };
 /* Given a binary tree, print its nodes according to the
 "bottom-up" postorder traversal. */
 void printPostorder( struct Node* node)
 {
    if (node == NULL)
        return ; 
    // first recur on left subtree
    printPostorder(node->left);
    // then recur on right subtree
    printPostorder(node->right);
    // now deal with the node
    cout << node->data << " " ;
 }
 /* Given a binary tree, print its nodes in inorder*/
 void printInorder( struct Node* node)
 {
    if (node == NULL)
        return ; 
    /* first recur on left child */
    printInorder(node->left);
    /* then print the data of node */
    cout << node->data << " " ; 
    /* now recur on right child */
    printInorder(node->right);
 }
 /* Given a binary tree, print its nodes in preorder*/
 void printPreorder( struct Node* node)
 {
    if (node == NULL)
        return ; 
    /* first print data of node */
    cout << node->data << " " ; 
    /* then recur on left sutree */
    printPreorder(node->left);
    /* now recur on right subtree */
    printPreorder(node->right);
 }
 /* Driver program to test above functions*/
 int main()
 {
    struct Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5); 
    cout << "
Preorder traversal of binary tree is 
" ;
    printPreorder(root);
    cout << "
Inorder traversal of binary tree is 
" ;
    printInorder(root);
    cout << "
Postorder traversal of binary tree is 
" ;
    printPostorder(root);
    return 0;
 }

C

 // C program for different tree traversals
 #include <stdio.h>
 #include <stdlib.h>
 /* A binary tree node has data, pointer to left child
   and a pointer to right child */
 struct node {
    data; int
    struct node* left;
    struct node* right;
 };
 /* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
 struct node* newNode( data) int
 {
    struct node* node
        = ( struct node*) malloc ( sizeof ( struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return (node);
 }
 /* Given a binary tree, print its nodes according to the
  "bottom-up" postorder traversal. */
 void printPostorder( struct node* node)
 {
    if (node == NULL)
        return ; 
    // first recur on left subtree
    printPostorder(node->left);
    // then recur on right subtree
    printPostorder(node->right);
    // now deal with the node
    printf ( "%d " , node->data);
 }
 /* Given a binary tree, print its nodes in inorder*/
 void printInorder( struct node* node)
 {
    if (node == NULL)
        return ; 
    /* first recur on left child */
    printInorder(node->left);
    /* then print the data of node */
    printf ( "%d " , node->data); 
    /* now recur on right child */
    printInorder(node->right);
 }
 /* Given a binary tree, print its nodes in preorder*/
 void printPreorder( struct node* node)
 {
    if (node == NULL)
        return ; 
    /* first print data of node */
    printf ( "%d " , node->data); 
    /* then recur on left sutree */
    printPreorder(node->left);
    /* now recur on right subtree */
    printPreorder(node->right);
 }
 /* Driver program to test above functions*/
 int main()
 {
    struct node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    printf ( "
Preorder traversal of binary tree is 
" );
    printPreorder(root);
    printf ( "
Inorder traversal of binary tree is 
" );
    printInorder(root);
    printf ( "
Postorder traversal of binary tree is 
" );
    printPostorder(root);
    getchar ();
    return 0;
 }

Python

 # Python program to for tree traversals
 # A class that represents an individual node in a
 # Binary Tree
 class Node:
    def __init__( self , key):
        self .left = None
        self .right = None
        self .val = key 
 # A function to do inorder tree traversal
 def printInorder(root): 
    if root: 
        # First recur on left child
        printInorder(root.left)
        # then print the data of node
        print (root.val), 
        # now recur on right child
        printInorder(root.right)
 # A function to do postorder tree traversal
 def printPostorder(root): 
    if root: 
        # First recur on left child
        printPostorder(root.left)
        # the recur on right child
        printPostorder(root.right)
        # now print the data of node
        print (root.val), 
 # A function to do preorder tree traversal
 def printPreorder(root): 
    if root: 
        # First print the data of node
        print (root.val), 
        # Then recur on left child
        printPreorder(root.left)
        # Finally recur on right child
        printPreorder(root.right)
 # Driver code
 root = Node( 1 )
 root.left = Node( 2 )
 root.right = Node( 3 )
 root.left.left = Node( 4 )
 root.left.right = Node( 5 )
 print "Preorder traversal of binary tree is"
 printPreorder(root)
 print "
Inorder traversal of binary tree is"
 printInorder(root)
 print "
Postorder traversal of binary tree is"
 printPostorder(root)

Джава

 // Java program for different tree traversals
 /* Class containing left and right child of current
   node and key value*/
 class Node {
    int key;
    Node left, right;
    public Node( int item)
    {
        key = item;
        left = right = null ;
    }
 }
 class BinaryTree {
    // Root of Binary Tree
    Node root;
    BinaryTree() { root = null ; } 
    /* Given a binary tree, print its nodes according to the
      "bottom-up" postorder traversal. */
    void printPostorder(Node node)
    {
        if (node == null )
            return ; 
        // first recur on left subtree
        printPostorder(node.left);
        // then recur on right subtree
        printPostorder(node.right);
        // now deal with the node
        System.out.print(node.key + " " );
    }
    /* Given a binary tree, print its nodes in inorder*/
    void printInorder(Node node)
    {
        if (node == null )
            return ; 
        /* first recur on left child */
        printInorder(node.left);
        /* then print the data of node */
        System.out.print(node.key + " " ); 
        /* now recur on right child */
        printInorder(node.right);
    }
    /* Given a binary tree, print its nodes in preorder*/
    void printPreorder(Node node)
    {
        if (node == null )
            return ; 
        /* first print data of node */
        System.out.print(node.key + " " ); 
        /* then recur on left sutree */
        printPreorder(node.left);
        /* now recur on right subtree */
        printPreorder(node.right);
    }
    // Wrappers over above recursive functions
    void printPostorder() { printPostorder(root); }
    void printInorder() { printInorder(root); }
    void printPreorder() { printPreorder(root); } 
    // Driver method
    public static void main(String[] args)
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node( 1 );
        tree.root.left = new Node( 2 );
        tree.root.right = new Node( 3 );
        tree.root.left.left = new Node( 4 );
        tree.root.left.right = new Node( 5 ); 
        System.out.println(
            "Preorder traversal of binary tree is " );
        tree.printPreorder();
        System.out.println(
            "
Inorder traversal of binary tree is " );
        tree.printInorder();
        System.out.println(
            "
Postorder traversal of binary tree is " );
        tree.printPostorder();
    }
 }

C #

 // C# program for different
 // tree traversals
 using System;
 /* Class containing left and
 right child of current
 node and key value*/
 class Node {
    public key; int
    public Node left, right; 
    public Node( int item)
    {
        key = item;
        left = right = null ;
    }
 }
 class BinaryTree {
    // Root of Binary Tree
    Node root;
    BinaryTree() { root = null ; } 
    /* Given a binary tree, print
       its nodes according to the
       "bottom-up" postorder traversal. */
    void printPostorder(Node node)
    {
        if (node == null )
            return ; 
        // first recur on left subtree
        printPostorder(node.left);
        // then recur on right subtree
        printPostorder(node.right);
        // now deal with the node
        Console.Write(node.key + " " );
    }
    /* Given a binary tree, print
       its nodes in inorder*/
    void printInorder(Node node)
    {
        if (node == null )
            return ; 
        /* first recur on left child */
        printInorder(node.left);
        /* then print the data of node */
        Console.Write(node.key + " " ); 
        /* now recur on right child */
        printInorder(node.right);
    }
    /* Given a binary tree, print
       its nodes in preorder*/
    void printPreorder(Node node)
    {
        if (node == null )
            return ; 
        /* first print data of node */
        Console.Write(node.key + " " ); 
        /* then recur on left sutree */
        printPreorder(node.left);
        /* now recur on right subtree */
        printPreorder(node.right);
    }
    // Wrappers over above recursive functions
    void printPostorder() { printPostorder(root); }
    void printInorder() { printInorder(root); }
    void printPreorder() { printPreorder(root); } 
    // Driver Code
    static public void Main(String[] args)
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5); 
        Console.WriteLine( "Preorder traversal "
                          + "of binary tree is " );
        tree.printPreorder();
        Console.WriteLine( "
Inorder traversal "
                          + "of binary tree is " );
        tree.printInorder();
        Console.WriteLine( "
Postorder traversal "
                          + "of binary tree is " );
        tree.printPostorder();
    }
 }
 // This code is contributed by Arnab Kundu

Javascript

 <script>
 // javascript program for different tree traversals
 /* Class containing left and right child of current
   node and key value*/
 class Node {
    constructor(val) {
        this .key = val;
        this .left = null ;
        this .right = null ;
    }
 }
    // Root of Binary Tree

                    
                                            Статьи
                                    
РЕКОМЕНДУЕМЫЕ СТАТЬИКак повысить эффективность вашего сайта: комплексный подход
28 Июня, 2025
Как создать интерактивный сайт без навыков программирования
23 Июня, 2025
Как создать интерактивный сайт без навыков программирования
23 Июня, 2025
Как создать эффективный сайт: от идеи до запуска
19 Июня, 2025
Гибридные СХД — баланс скорости и объема для современного бизнеса
21 Мая, 2025
Мобильная разработка в 2025 году: как выбрать между нативным и кроссплатформенным подходом
21 Мая, 2025
Как виртуальные номера меняют бизнес-коммуникации IT-компаний
17 Мая, 2025
Революция в SEO: Как инструменты массового открытия URL меняют правила игры
10 Мая, 2025