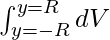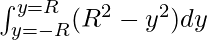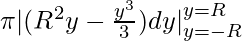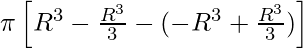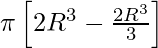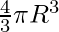Объем сферы

Объем сферы — это количество жидкости, которое может вместить сфера. Это пространство, занимаемое сферой в трехмерном пространстве. Измеряется в единицах ³ , т.е. м ³ , см ³ и т. д.

Сфера — это трехмерный твердый объект круглой формы в геометрии. С математической точки зрения это трехмерная комбинация группы точек, соединенных одной общей точкой на равных расстояниях. Сфера, в отличие от других трехмерных фигур, не имеет ни вершин, ни краев. Его центр равноудален от всех мест на его поверхности. Другими словами, расстояние между центром сферы и любой точкой на ее поверхности одинаково. В повседневной жизни используются различные сферические объекты: футбол, баскетбол, Земля, Луна и т. д.

Что такое Объем сферы?

Объем сферы — это количество места, которое она занимает внутри себя. Сфера представляет собой трехмерную круглую твердую форму, в которой все точки на ее поверхности находятся на равном расстоянии от ее центра. Фиксированное расстояние известно как радиус сферы, а фиксированная точка известна как центр сферы. Мы заметим изменение формы, когда круг повернется. В результате вращения двумерного объекта, известного как круг, получается трехмерная форма сферы.

Формула объема шара дается,

V = 4/3πr³

where,

r = radius of the sphere

π = 22/7

Формула объема сферы с ее выводом

Используя интеграционный подход, мы можем просто вычислить объем сферы.

Suppose the sphere’s volume is made up of a series of thin circular discs stacked one on top of the other, as drawn in the diagram above. Each thin disc has a radius of r and a thickness of dy that is y distance from the x-axis.

Let the volume of a disc be dV. The value of dV is given by,

dV = (πr²)dy

dV = π (R² – y²)dy

The total volume of the sphere will be the sum of volumes of all these small discs. The required value can be obtained by integrating the expression from limit -R to R.

So, the volume of sphere becomes,

V = 

= 

= 

= 

= 

= 

Thus, the formula for volume of sphere is derived.

Как рассчитать объем сферы?

Объем сферы – это пространство, занимаемое сферой. Его объем можно рассчитать по формуле V = 4/3πr ³ . Шаги, необходимые для вычисления объема сферы:

1. Отметьте значение радиуса сферы.
2. Найдите куб радиуса.
3. Умножьте куб радиуса на (4/3)π
4. Добавьте единицу к окончательному ответу.

Пример: Найдите объем шара радиусом 7 см.

Решение:

The formula for volume of a sphere, V = (4/3)πr³
Given, r = 7 cm
Volume of sphere, V = ((4/3) × π × 7³) cm³
V = 1436.8 cm³ 
Thus, the volume of sphere is 1436.8 cm³

Статьи по Теме

• Volume of Cone
• Volume of Cube
• Volume of Cylinder

Решенные примеры по объему сферы

Пример 1. Найдите объем сферы, радиус которой равен 9 см.

Решение:

We have, r = 9.

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (9) (9) (9)

= (4) (3.14) (3) (9) (9)

= 3052 cm³

Пример 2. Найдите объем сферы, радиус которой равен 12 см.

Решение:

We have, r = 12

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (12) (12) (12)

= (4) (3.14) (4) (12) (12)

= 7234.56 cm³

Пример 3. Найдите объем сферы, радиус которой равен 6 см.

Решение:

We have, r = 6.

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (6) (6) (6)

= (4) (3.14) (2) (6) (6)

= 904.32 cm³

Пример 4. Найдите объем сферы, радиус которой равен 4 см.

Решение:

We have, r = 4.

Volume of sphere = 4/3 πr3

= (4/3) (3.14) (4) (4) (4)

= (1.33) (3.14) (4) (4) (4)

= 267.27 cm³

Пример 5. Найдите объем шара, диаметр которого равен 10 см.

Решение:

We have, 2r = 10

=> r = 10/2

=> r = 5

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (5) (5) (5)

= (1.33) (3.14) (5) (5) (5)

= 522.025 cm³

Пример 6. Найдите объем шара, диаметр которого равен 16 см.

Решение:

We have, 2r = 16

=> r = 16/2

=> r = 8

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (8) (8) (8)

= (1.33) (3.14) (8) (8) (8)

= 2138.21 cm³

Пример 7. Найдите объем шара, диаметр которого равен 14 см.

Решение:

We have, 2r = 14

=> r = 14/2

=> r = 7

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (7) (7) (7)

= (1.33) (3.14) (7) (7) (7)

= 1432.43 cm³

Часто задаваемые вопросы о томе сферы

Вопрос 1: Напишите формулу полной поверхности шара.

Отвечать:

Total surface area of any sphere is given by:

Area = 4πr²

where ‘r’ is the radius of the given sphere.

Вопросы 2: Какова формула объема сферы?

Отвечать:

The volume of a sphere is given by:

Volume = 4/3πr³

where ‘r’ is the radius of the given sphere.

Вопрос 3: Как найти объем полусферы?

Отвечать:

The volume of a hemi-sphere is given by:

Volume = 2/3πr³

where ‘r’ is the radius of the given sphere.

Вопрос 4: Если сфера и полусфера имеют одинаковые радиусы, то каково отношение их объемов?

Отвечать:

If a sphere and a hemisphere have the same radii then the ratio of their volume is given by

V₁ : V₂ =  (4/3πr³) : (2/3πr³)

          = 2 : 1

Вопрос 5: Как измерить объем Сферы?

Отвечать:

The Volume of the Sphere is measured in m³, cm³, litres, etc.

m³ is the standard unit of measurement.