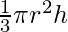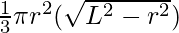Объем конуса

Объем конуса можно описать как пространство, занимаемое конусом, или как емкость конуса. Конус — это трехмерный объект, имеющий круглое плоское основание и заостренную вершину, называемую вершиной или вершиной. Конусом считается фигура, образованная неконгруэнтным круговым диском, который становится меньше и является точкой только на вершине.

Конус представляет собой твердый трехмерный геометрический объект с круглым основанием и острым краем наверху, известным как вершина. Он имеет одну грань и одну вершину. У конуса нет ребер. Это форма с изогнутой вершиной и круглым основанием. У конуса одна грань, одна вершина и нет ребер. Его наклонная высота — это длина отрезка от вершины конуса до любой точки на окружности основания конуса. Прямой круговой конус — это конус, вершина которого находится прямо над круглым основанием на перпендикулярном расстоянии. Наклонный конус - это конус, вершина которого не находится непосредственно над круглым основанием. Кроме того, здесь найдите площадь поверхности прямого круглого конуса.

Каков объем конуса?

Объем конуса определяется как количество пространства или емкости, которую он заполняет. Объем конуса измеряется в кубических единицах, таких как см ³ , м ³ , дюйм ³ и так далее. Вращая треугольник вокруг любой из его вершин, можно получить конус. Объем конуса также можно измерять в литрах.

Формула объема конуса

Конус представляет собой твердую трехмерную форму, имеющую круглое основание. У него изогнутая поверхность. Высота перпендикуляра - это расстояние от основания до вершины. Конус можно разделить на два типа: прямые круглые конусы и наклонные конусы. Вершина прямого кругового конуса находится вертикально над центром основания, но вершина косого конуса не находится вертикально над центром основания.

Формула объема конуса находится по формуле:

V = 

where,

r = radius of the cone,

h = height of the cone,

π = 22/7

Also, the relationship between the cone’s volume and slant height by applying Pythagoras’ theorem to it is given by,

h² + r² = L²

=> h = √(L² – r²)

Hence, the volume of cone in terms of its slant height is given by,

V = 

Объем производной конуса

Предположим, у нас есть конус с круглым основанием, радиус которого равен r, а высота равна h.

We know that the volume of a cone is equal to one-third of the volume of a cylinder having the same base radius and height.

So, the volume becomes,

V = 1/3 x Circular Base area x Height

= 1/3 x πr² x h

=  πr²h/3

This derives the formula for volume of cone.

Как найти объем конуса?

Рассмотрим пример для определения объема конуса.

Пример: Определите объем конуса, если радиус его круглого основания равен 3 см, а высота 5 см.

Step 1: Note the radius of the circular base (r) and the height of the cone (h). Here, the radius is 3 cm and the height is 5 cm.

Step 2: Calculate the area of the circular base = πr². Substitute the value of r and π in the given equation, i.e., 3.14 × (3)² = 28.26 cm².

Step 3: We know that the volume of a cone is (1/3) × (area of the circular base) × height of the cone. So, substitute the values in the equation = (1/3) × 28.26 × 5 = 47.1 cm³.

Step 4: Hence, the volume of the given cone is 47.1 cm³.

Используя шаги, описанные выше, можно рассчитать объем конуса.

Объем куска конуса

Усеченный конус — это срезанная часть конуса, объем усеченного конуса — это количество жидкости, которое может вместить любой усеченный конус. Итак, для расчета объема нам нужно найти разность объемов двух конусов. Для получения более подробной информации о Frustum of Cone нажмите здесь.

Формула объема куска конуса

Формула для нахождения объема усеченного конуса дается путем вычитания объема двух конусов. Изучите данную фигуру, чтобы найти объем усеченного конуса.

Из рисунка выше мы имеем общую высоту H' = H+h и общую высоту наклона L =l ₁ +l ₂ . Радиус конуса = R и радиус срезанного конуса = r. Теперь объем большего конуса = 1/3 π R ² H' = 1/3 π R ² (H+h)

Объем меньшего конуса = 1/3 πr ² ч. Объем усеченного конуса можно рассчитать по разнице между двумя конусами, т.е.

Объем усеченного конуса = 1/3 π R ² H' -1/3 πr ² ч
= 1/3π R ² (H+h) -1/3 πr ² ч
=1/3 π [ R ² (H+h)-r ² h ] ………(1)

Используя свойства подобных треугольников в Δ QPS и Δ QAB. у нас есть,
R/ r = Н+ч/ч
H+h = (Rh)/r.
Подставляя значение H+h в формулу объема усеченной пирамиды, получаем,

Объем куска = 1/3 π [ R ² (Rh/r)-r ² h ]
= 1/3 π [R ³ ч/rr ² ч]
= 1/3 π ч (R ³ /rr ² )
= 1/3 π h (R ³ -r ³ /r)

Volume of Frustum of Cone = 1/3 π h [(R³-r³)/ r]

Решенный пример на объеме конуса

Пример 1. Найти объем конуса для радиуса 7 см и высоты 14 см.

Решение:

We have, r = 7 and h = 14.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (7) (7) (14)

= (1/3) (7) (7) (2)

= 32.66 cm³

Пример 2. Найти объем конуса для радиуса 5 см и высоты 9 см.

Решение:

We have, r = 5 and h = 9.

Volume of cone = 1/3 πr²h

= (1/3) (3.14) (5) (5) (9)

= (3.14) (5) (5) (3)

= 235.49 cm³

Пример 3. Найдите объем конуса для радиуса 7 см и высоты 12 см.

Решение:

We have, r = 7 and h = 12.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (7) (7) (12)

= (22) (7) (4)

= 616 cm³

Пример 4. Найдите объем конуса радиусом 8 см и высотой 15 см.

Решение:

We have, r = 8 and h = 15.

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (8) (8) (15)

= (1/3) (22/7) (8) (8) (5)

= 335.02 cm³

Пример 5. Найдите объем конуса при диаметре 24 см и наклонной высоте 13 см.

Решение:

We have, 2r = 24

=> r = 24/2

=> r = 12

Also, l = 13.

Volume of cone = 1/3 πr² √(l² – r²)

= (1/3) (22/7) (12) (12) (√(13² – 12²)

= (1/3) (22/7) (12) (12) (5)

= 754.28 cm³

Пример 6. Найдите объем конуса при диаметре 16 см и наклонной высоте 10 см.

Решение:

We have, 2r = 16

=> r = 16/2

=> r = 8

Also, l = 10.

Volume of cone = 1/3 πr² √(l² – r²)

= (1/3) (22/7) (8) (8) (√(10² – 8²)

= (1/3) (22/7) (8) (8) (6)

= 402.048 cm³

Пример 7. Найти объем конуса при высоте 8 см и наклонной высоте 17 см.

Решение:

We have h = 8 and l = 10.

Find the value of r.

r = √(l² – h²)

= √(17² – 8²)

= √(289 – 64)

= 15

Volume of cone = 1/3 πr²h

= (1/3) (22/7) (15) (15) (8)

= (1/3) (22/7) (5) (15) (8)

= 1884.6 cm³

Часто задаваемые вопросы об объеме конуса

Вопрос 1: Что произойдет с объемом конуса, если его радиус и высоту удвоить?

Отвечать:

If r = 2r and h = 2h,

then the volume of a cone is given as:

Volume of a cone = (1/3)π(2r)²(2h) cubic units

                        V = (⅓)π(4r²)(2h)

                        V = (8/3)πr²h

Thus, volume of a cone becomes 8 times the original volume i.e. V = (8/3)πr²h,

when its radius and height are doubled.

Вопрос 2: Какова формула полной площади поверхности конуса?

Отвечать:

Total surface area of a cone is given by the formula πr(l + r) square units, where r is the radius of the circular base and l is the slant height of the cone.

Вопрос 3: Какова формула объема конуса?

Отвечать:

Volume of a cone is given by the formula ⅓ πr² x h cubic units, where r is the radius of the circular base and h is the height of the cone.

Вопрос 4: Найдите соотношение между объемом цилиндра и объемом конуса.

Отвечать:

One-third of the volume of a cylinder is equal to the volume of a cone, having the same radius and height.

Вопрос 5: Какова формула для наклонной высоты конуса?

Отвечать:

The slant height of a cone l = √(h2 + r2), where h is the height of the cone and r is the radius of the circular base.

Вопрос 6: Каков будет объем конуса, если его радиус и высоту уменьшить вдвое?

Отвечать:

If r = r/2 and h = h/2,

then the volume of a cone is given as:

Volume of a cone = (1/3)π(r/2)²(h/2) cubic units

                        V = (⅓)π(r²/4)(h/2)

                        V = (1/24)πr²h

Thus, volume of a cone becomes 1/8 times the original volume i.e. V = (1/24)πr²h,

when its radius and height are halfed.

Вопрос 7: Как найти объем конуса, если известны высота и диаметр конуса?

Отвечать:

Given,

Volume of a cone = (1/3)πr²h cubic units

Where r is radius and h is height

Since (radius)r = (diameter)d/2, 

the volume of a cone becomes

V = (1/3)π(d/2)²h cubic units

V = (1/12)πd²h cubic units.

Hence, the formula for the volume of a cone is (1/12)πd²h cubic units, if its height and diameter are given.

Связанные ресурсы

• Surface Area of a Cone
• Volume of Sphere