Найдите максимальный узел на заданном уровне в двоичном дереве

Опубликовано: 24 Января, 2022

Учитывая двоичное дерево и уровень . Задача - найти узел с максимальным значением на данном уровне.

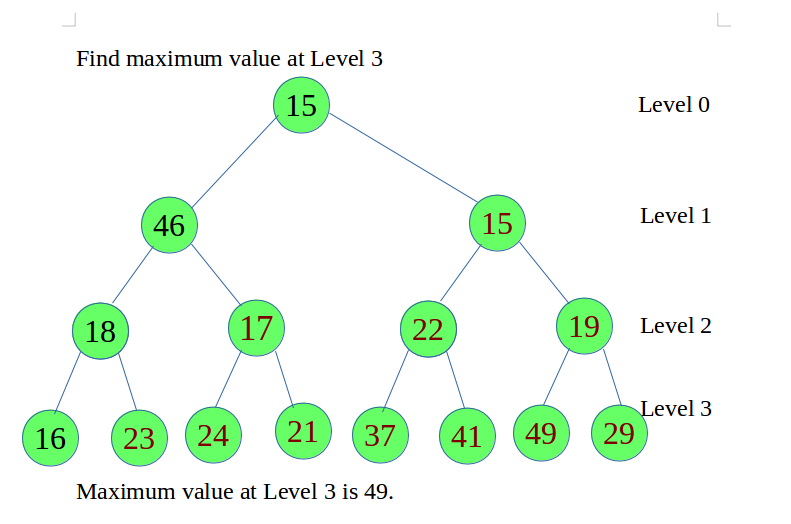
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Идея состоит в том, чтобы рекурсивно перемещаться по дереву по глубине и возвращать узлы после достижения требуемого уровня, а затем возвращать максимум левого и правого поддеревьев для каждого последующего вызова. Таким образом, последний вызов вернет узел с максимальным значением среди всех узлов на данном уровне.
Ниже представлен пошаговый алгоритм:

  1. Выполните обход DFS и каждый раз уменьшайте значение level на 1 и продолжайте рекурсивно обходить левое и правое поддеревья.
  2. Когда значение level становится равным 0, это означает, что мы находимся на заданном уровне, затем возвращаем root-> data.
  3. Найдите максимум между двумя значениями, возвращаемыми левым и правым поддеревьями, и верните максимум.

Below is the implementation of above approach: 

C++

// CPP program to find the node with
// maximum value at a given level
 
#include <iostream>
 
using namespace std;
 
// Tree node
struct Node {
    int data;
    struct Node *left, *right;
};
 
// Utility function to create a new Node
struct Node* newNode(int val)
{
    struct Node* temp = new Node;
    temp->left = NULL;
    temp->right = NULL;
    temp->data = val;
    return temp;
}
 
// function to find the maximum value
// at given level
int maxAtLevel(struct Node* root, int level)
{
    // If the tree is empty
    if (root == NULL)
        return 0;
 
    // if level becomes 0, it means we are on
    // any node at the given level
    if (level == 0)
        return root->data;
 
    int x = maxAtLevel(root->left, level - 1);
    int y = maxAtLevel(root->right, level - 1);
 
    // return maximum of two
    return max(x, y);
}
 
// Driver code
int main()
{
    // Creating the tree
    struct Node* root = NULL;
    root = newNode(45);
    root->left = newNode(46);
    root->left->left = newNode(18);
    root->left->left->left = newNode(16);
    root->left->left->right = newNode(23);
    root->left->right = newNode(17);
    root->left->right->left = newNode(24);
    root->left->right->right = newNode(21);
    root->right = newNode(15);
    root->right->left = newNode(22);
    root->right->left->left = newNode(37);
    root->right->left->right = newNode(41);
    root->right->right = newNode(19);
    root->right->right->left = newNode(49);
    root->right->right->right = newNode(29);
 
    int level = 3;
 
    cout << maxAtLevel(root, level);
 
    return 0;
}

Java

// Java program to find the
// node with maximum value
// at a given level
import java.util.*;
class GFG
{
 
// Tree node
static class Node
{
    int data;
    Node left, right;
}
 
// Utility function to
// create a new Node
static Node newNode(int val)
{
    Node temp = new Node();
    temp.left = null;
    temp.right = null;
    temp.data = val;
    return temp;
}
 
// function to find
// the maximum value
// at given level
static int maxAtLevel(Node root, int level)
{
    // If the tree is empty
    if (root == null)
        return 0;
 
    // if level becomes 0,
    // it means we are on
    // any node at the given level
    if (level == 0)
        return root.data;
 
    int x = maxAtLevel(root.left, level - 1);
    int y = maxAtLevel(root.right, level - 1);
 
    // return maximum of two
    return Math.max(x, y);
}
 
// Driver code
public static void main(String args[])
{
    // Creating the tree
    Node root = null;
    root = newNode(45);
    root.left = newNode(46);
    root.left.left = newNode(18);
    root.left.left.left = newNode(16);
    root.left.left.right = newNode(23);
    root.left.right = newNode(17);
    root.left.right.left = newNode(24);
    root.left.right.right = newNode(21);
    root.right = newNode(15);
    root.right.left = newNode(22);
    root.right.left.left = newNode(37);
    root.right.left.right = newNode(41);
    root.right.right = newNode(19);
    root.right.right.left = newNode(49);
    root.right.right.right = newNode(29);
 
    int level = 3;
 
    System.out.println(maxAtLevel(root, level));
}
}
 
// This code is contributed
// by Arnab Kundu

Python3

# Python3 program to find the node 
# with maximum value at a given level
 
# Helper function that allocates a new
# node with the given data and None
# left and right poers.                                    
class newNode:
 
    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
# function to find the maximum 
# value at given level
def maxAtLevel(root, level):
 
    # If the tree is empty
    if (root == None) :
        return 0
 
    # if level becomes 0, it means we
    # are on any node at the given level
    if (level == 0) :
        return root.data
 
    x = maxAtLevel(root.left, level - 1)
    y = maxAtLevel(root.right, level - 1)
 
    # return maximum of two
    return max(x, y)
     
# Driver Code
if __name__ == "__main__":
 
    """
    Let us create Binary Tree shown
    in above example """
    root = newNode(45)
    root.left = newNode(46)
    root.left.left = newNode(18)
    root.left.left.left = newNode(16)
    root.left.left.right = newNode(23)
    root.left.right = newNode(17)
    root.left.right.left = newNode(24)
    root.left.right.right = newNode(21)
    root.right = newNode(15)
    root.right.left = newNode(22)
    root.right.left.left = newNode(37)
    root.right.left.right = newNode(41)
    root.right.right = newNode(19)
    root.right.right.left = newNode(49)
    root.right.right.right = newNode(29)
    level = 3
    print(maxAtLevel(root, level))
 
# This code is contributed by
# Shubham Singh(SHUBHAMSINGH10)

C#

// C# program to find the
// node with maximum value
// at a given level
using System;
 
class GFG
{
 
    // Tree node
    class Node
    {
        public int data;
        public Node left, right;
    }
 
    // Utility function to
    // create a new Node
    static Node newNode(int val)
    {
        Node temp = new Node();
        temp.left = null;
        temp.right = null;
        temp.data = val;
        return temp;
    }
 
    // function to find
    // the maximum value
    // at given level
    static int maxAtLevel(Node root, int level)
    {
        // If the tree is empty
        if (root == null)
            return 0;
 
        // if level becomes 0,
        // it means we are on
        // any node at the given level
        if (level == 0)
            return root.data;
 
        int x = maxAtLevel(root.left, level - 1);
        int y = maxAtLevel(root.right, level - 1);
 
        // return maximum of two
        return Math.Max(x, y);
    }
 
    // Driver code
    public static void Main(String []args)
    {
        // Creating the tree
        Node root = null;
        root = newNode(45);
        root.left = newNode(46);
        root.left.left = newNode(18);
        root.left.left.left = newNode(16);
        root.left.left.right = newNode(23);
        root.left.right = newNode(17);
        root.left.right.left = newNode(24);
        root.left.right.right = newNode(21);
        root.right = newNode(15);
        root.right.left = newNode(22);
        root.right.left.left = newNode(37);
        root.right.left.right = newNode(41);
        root.right.right = newNode(19);
        root.right.right.left = newNode(49);
        root.right.right.right = newNode(29);
 
        int level = 3;
 
        Console.WriteLine(maxAtLevel(root, level));
    }
}
 
// This code is contributed by 29AjayKumar
Output

49
Структуры данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Различия между структурой данных массива и словаря
21 Января, 2023
TCS SDE Sheet: Вопросы и ответы для интервью
12 Января, 2023
Множественные сравнения в очереди приоритетов С++?
6 Января, 2023
Когда использовать Queue over ArrayList в Java?
6 Января, 2023
Введение в связанный список — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Введение в массивы — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Как подготовиться к ICFP или Международной конференции по функциональному программированию?
12 Декабря, 2022