Найдите количество пар идеальных узлов в данном дереве

Опубликовано: 7 Января, 2022

Учитывая дерево из N узлов и целое число K , каждый узел пронумерован от 1 до N. Задача - найти количество пар идеальных узлов в дереве.

Пара узлов (a, b) называется идеальной, если

  1. a является предком b .
  2. И, abs (a - b) ≤ K

Примеры:

 Вход:



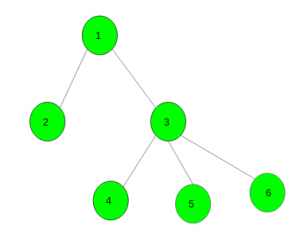
 К = 2
Выход: 4
(1, 2), (1, 3), (3, 4), (3, 5) - такие пары.

Входные данные: рассмотрим график в примере 1 и k = 3.
Выход: 6
Такими парами являются (1, 2), (1, 3), (1, 4), (3, 4), (3, 5), (3, 6).
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: во- первых, нам нужно пройти по дереву с помощью DFS, поэтому нам нужно найти корневой узел, узел без родителя. По мере прохождения каждого узла мы сохраняем его в структуре данных, чтобы отслеживать всех предков для следующего узла. Перед тем как это сделать, получите количество предков узла в диапазоне [presentNode - k, presentNode + k], затем добавьте его к общему количеству пар.
Нам нужна структура данных, которая может:

  1. Вставляйте узел по мере обхода дерева.
  2. По возвращении удалите узел.
  3. Укажите количество узлов в диапазоне [presentNode - k, PresentNode + k], которые были сохранены.

Двоичное индексированное дерево выполняет три вышеуказанные операции.
Мы можем выполнить указанные выше 3 операции, инициализировав все значения индекса BIT равными 0, а затем:

  1. Вставьте узел, обновив индекс этого узла до 1.
  2. Удалите узел, обновив индекс этого узла до 0.
  3. Получите количество похожих пар предка этого узла, запросив сумму диапазона [presentNode - k, PresentNode + k]

Below is the implementation of the above approach: 

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
#define N 100005
 
int n, k;
 
// Adjacency list
vector<int> al[N];
long long Ideal_pair;
long long bit[N];
bool root_node[N];
 
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
long long bit_q(int i, int j)
{
    long long sum = 0ll;
    while (j > 0) {
        sum += bit[j];
        j -= (j & (j * -1));
    }
    i--;
    while (i > 0) {
        sum -= bit[i];
        i -= (i & (i * -1));
    }
    return sum;
}
 
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
void bit_up(int i, long long diff)
{
    while (i <= n) {
        bit[i] += diff;
        i += i & -i;
    }
}
 
// DFS function to find ideal pairs
void dfs(int node)
{
    Ideal_pair += bit_q(max(1, node - k),
                        min(n, node + k));
    bit_up(node, 1);
    for (int i = 0; i < al[node].size(); i++)
        dfs(al[node][i]);
    bit_up(node, -1);
}
 
// Function for initialisation
void initalise()
{
    Ideal_pair = 0;
    for (int i = 0; i <= n; i++) {
        root_node[i] = true;
        bit[i] = 0LL;
    }
}
 
// Function to add an edge
void Add_Edge(int x, int y)
{
    al[x].push_back(y);
    root_node[y] = false;
}
 
// Function to find number of ideal pairs
long long Idealpairs()
{
    // Find root of the tree
    int r = -1;
    for (int i = 1; i <= n; i++)
        if (root_node[i]) {
            r = i;
            break;
        }
 
    dfs(r);
 
    return Ideal_pair;
}
 
// Driver code
int main()
{
    n = 6, k = 3;
 
    initalise();
 
    // Add edges
    Add_Edge(1, 2);
    Add_Edge(1, 3);
    Add_Edge(3, 4);
    Add_Edge(3, 5);
    Add_Edge(3, 6);
 
    // Function call
    cout << Idealpairs();
 
    return 0;
}

Java

// Java implementation of the approach
import java.util.*;
 
class GFG{
     
static final int N  = 100005;
 
static int n, k;
 
// Adjacency list
@SuppressWarnings("unchecked")
static Vector<Integer> []al = new Vector[N];
static long Ideal_pair;
static long []bit = new long[N];
static boolean []root_node = new boolean[N];
 
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
static long bit_q(int i, int j)
{
    long sum = 0;
    while (j > 0)
    {
        sum += bit[j];
        j -= (j & (j * -1));
    }
    i--;
    while (i > 0)
    {
        sum -= bit[i];
        i -= (i & (i * -1));
    }
    return sum;
}
 
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
static void bit_up(int i, long diff)
{
    while (i <= n)
    {
        bit[i] += diff;
        i += i & -i;
    }
}
 
// DFS function to find ideal pairs
static void dfs(int node)
{
    Ideal_pair += bit_q(Math.max(1, node - k),
                        Math.min(n, node + k));
    bit_up(node, 1);
     
    for(int i = 0; i < al[node].size(); i++)
        dfs(al[node].get(i));
         
    bit_up(node, -1);
}
 
// Function for initialisation
static void initalise()
{
    Ideal_pair = 0;
    for (int i = 0; i <= n; i++) {
        root_node[i] = true;
        bit[i] = 0;
    }
}
 
// Function to add an edge
static void Add_Edge(int x, int y)
{
    al[x].add(y);
    root_node[y] = false;
}
 
// Function to find number of ideal pairs
static long Idealpairs()
{
     
    // Find root of the tree
    int r = -1;
    for(int i = 1; i <= n; i++)
        if (root_node[i])
        {
            r = i;
            break;
        }
 
    dfs(r);
 
    return Ideal_pair;
}
 
// Driver code
public static void main(String[] args)
{
    n = 6;
    k = 3;
     
    for(int i = 0; i < al.length; i++)
        al[i] = new Vector<Integer>();
         
    initalise();
 
    // Add edges
    Add_Edge(1, 2);
    Add_Edge(1, 3);
    Add_Edge(3, 4);
    Add_Edge(3, 5);
    Add_Edge(3, 6);
 
    // Function call
    System.out.print(Idealpairs());
}
}
 
// This code is contributed by Amit Katiyar

Python3

# Python3 implementation of the approach
N = 100005
Ideal_pair = 0
 
# Adjacency list
al = [[] for i in range(100005)]
bit = [0 for i in range(N)]
root_node = [0 for i in range(N)]
 
# bit : bit array
# i and j are starting and
# ending index INCLUSIVE
def bit_q(i, j):
    sum = 0
    while (j > 0):
        sum += bit[j]
        j -= (j & (j * -1))
     
    i -= 1
    while (i > 0):
        sum -= bit[i]
        i -= (i & (i * -1))
    return sum
 
# bit : bit array
# n : size of bit array
# i is the index to be updated
# diff is (new_val - old_val)
def bit_up(i, diff):
    while (i <= n):
        bit[i] += diff
        i += i & -i
 
# DFS function to find ideal pairs
def dfs(node, x):
    Ideal_pair = x
    Ideal_pair += bit_q(max(1, node - k),
                        min(n, node + k))
    bit_up(node, 1)
    for i in range(len(al[node])):
        Ideal_pair = dfs(al[node][i], Ideal_pair)
    bit_up(node, -1)
     
    return Ideal_pair
     
# Function for initialisation
def initalise():
    Ideal_pair = 0;
    for i in range(n + 1):
        root_node[i] = True
        bit[i] = 0
 
# Function to add an edge
def Add_Edge(x, y):
    al[x].append(y)
    root_node[y] = False
 
# Function to find number of ideal pairs
def Idealpairs():
     
    # Find root of the tree
    r = -1
    for i in range(1, n + 1, 1):
        if (root_node[i]):
            r = i
            break
 
    Ideal_pair = dfs(r, 0)
 
    return Ideal_pair
 
# Driver code
if __name__ == "__main__":
    n = 6
    k = 3
 
    initalise()
 
    # Add edges
    Add_Edge(1, 2)
    Add_Edge(1, 3)
    Add_Edge(3, 4)
    Add_Edge(3, 5)
    Add_Edge(3, 6)
 
    # Function call
    print(Idealpairs())
 
# This code is contributed by
# Surendra_Gangwar

C#

// C# implementation of the
// above approach
using System;
using System.Collections.Generic;
class GFG{
     
static readonly int N  = 100005;
 
static int n, k;
 
// Adjacency list
static List<int> []al =
       new List<int>[N];
static long Ideal_pair;
static long []bit =
       new long[N];
static bool []root_node =
       new bool[N];
 
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
static long bit_q(int i,
                  int j)
{
  long sum = 0;
  while (j > 0)
  {
    sum += bit[j];
    j -= (j & (j * -1));
  }
  i--;
  while (i > 0)
  {
    sum -= bit[i];
    i -= (i & (i * -1));
  }
  return sum;
}
 
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
static void bit_up(int i,
                   long diff)
{
  while (i <= n)
  {
    bit[i] += diff;
    i += i & -i;
  }
}
 
// DFS function to find
// ideal pairs
static void dfs(int node)
{
  Ideal_pair += bit_q(Math.Max(1,
                               node - k),
                      Math.Min(n,
                               node + k));
  bit_up(node, 1);
 
  for(int i = 0;
          i < al[node].Count; i++)
    dfs(al[node][i]);
 
  bit_up(node, -1);
}
 
// Function for
// initialisation
static void initalise()
{
  Ideal_pair = 0;
  for (int i = 0; i <= n; i++)
  {
    root_node[i] = true;
    bit[i] = 0;
  }
}
 
// Function to add an edge
static void Add_Edge(int x,
                     int y)
{
  al[x].Add(y);
  root_node[y] = false;
}
 
// Function to find number
// of ideal pairs
static long Idealpairs()
{    
  // Find root of the tree
  int r = -1;
   
  for(int i = 1; i <= n; i++)
    if (root_node[i])
    {
      r = i;
      break;
    }
Олимпиады по программированию Структуры данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Различия между структурой данных массива и словаря
21 Января, 2023
TCS SDE Sheet: Вопросы и ответы для интервью
12 Января, 2023
Настройка Sublime Text для соревновательного программирования (C++) с использованием плагина Fast Olympic Coding
8 Января, 2023
Множественные сравнения в очереди приоритетов С++?
6 Января, 2023
Когда использовать Queue over ArrayList в Java?
6 Января, 2023
Введение в связанный список — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Введение в массивы — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022