ML | Определите оптимальное значение K в кластеризации K-средних

Опубликовано: 25 Июля, 2021

Предпосылка: Кластеризация K-средних | Вступление

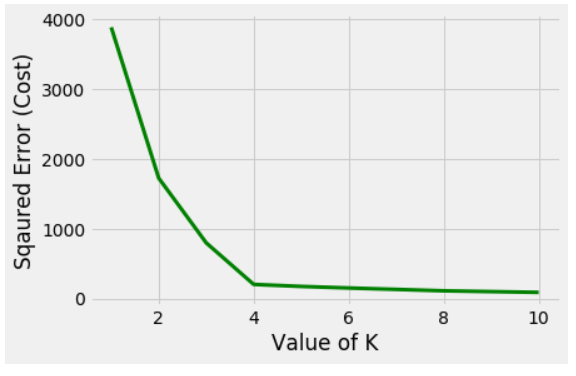
Существует популярный метод, известный как метод локтя, который используется для определения оптимального значения K для выполнения алгоритма кластеризации K-средних. Основная идея этого метода состоит в том, что он отображает различные значения затрат при изменении k . По мере увеличения значения K в кластере будет меньше элементов. Таким образом, среднее искажение уменьшится. Меньшее количество элементов означает ближе к центроиду. Итак, точка, в которой это искажение уменьшается больше всего, - это точка локтя .

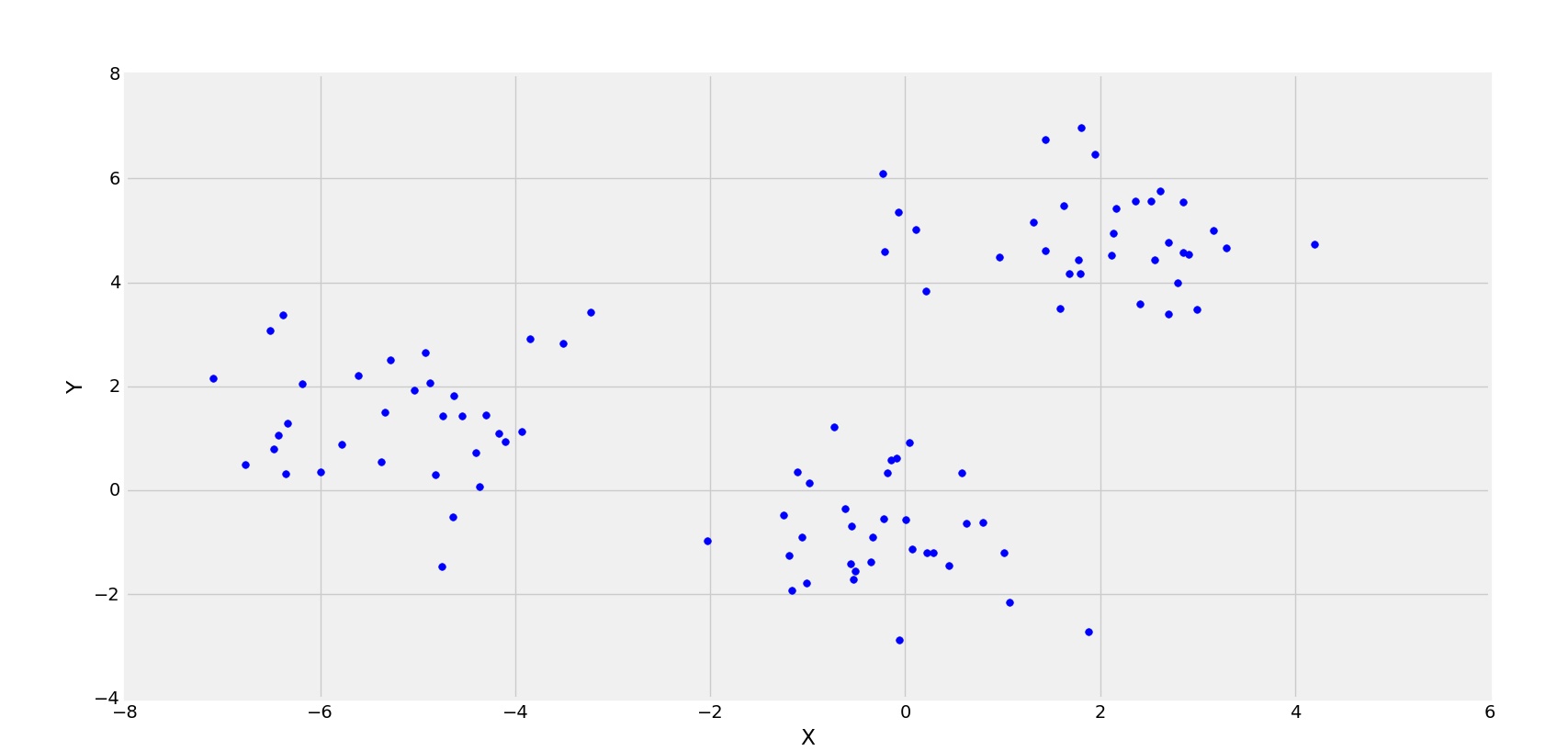
Формируются 3 кластера

На приведенном выше рисунке ясно видно, что распределение точек формирует 3 кластера. Теперь посмотрим на график квадратичной ошибки (Стоимость) для различных значений K.

Колено формируется при К = 3

Ясно, что колено формируется при K = 3. Таким образом, оптимальное значение будет 3 для выполнения K-средних.

Еще один пример с 4 кластерами.

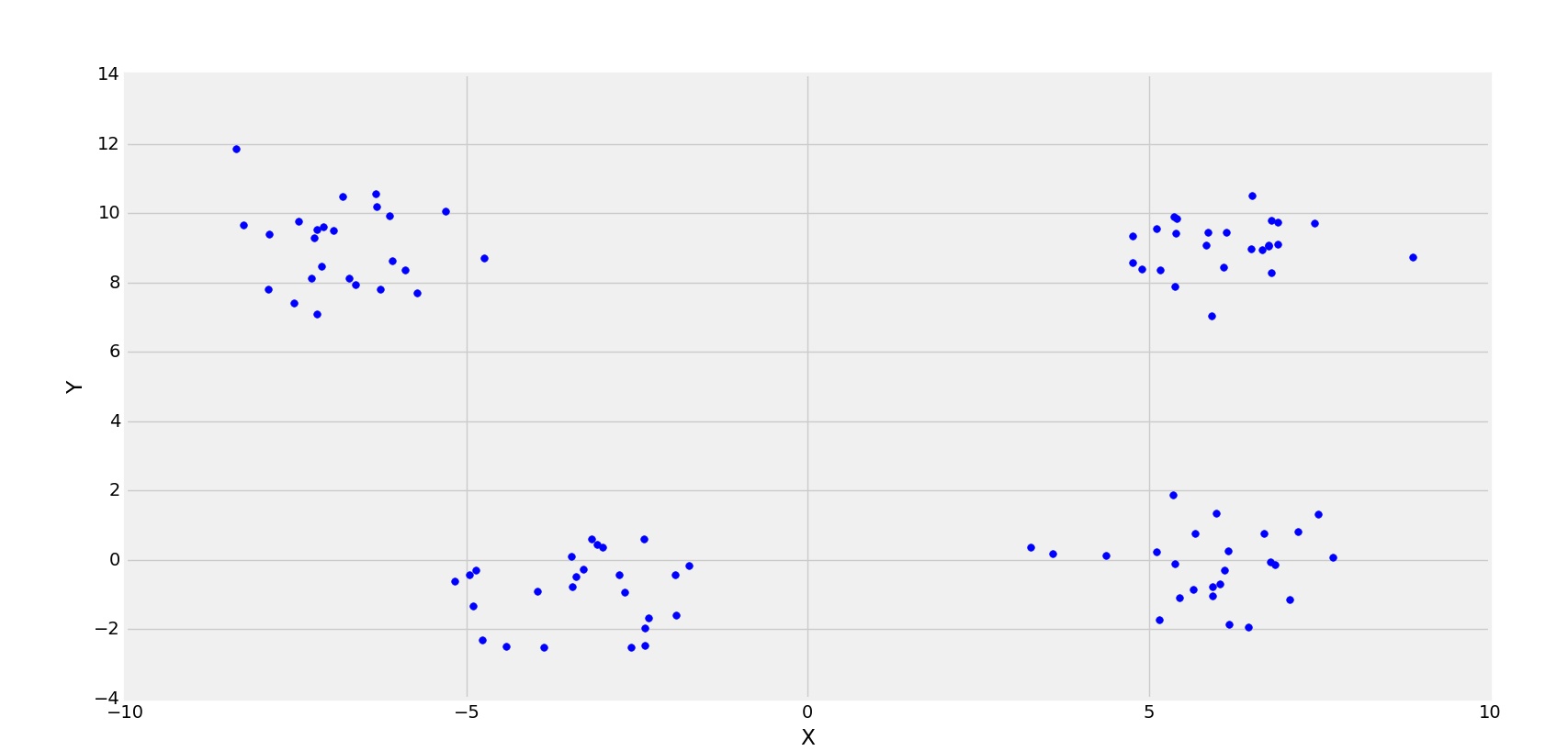
4-кластеры

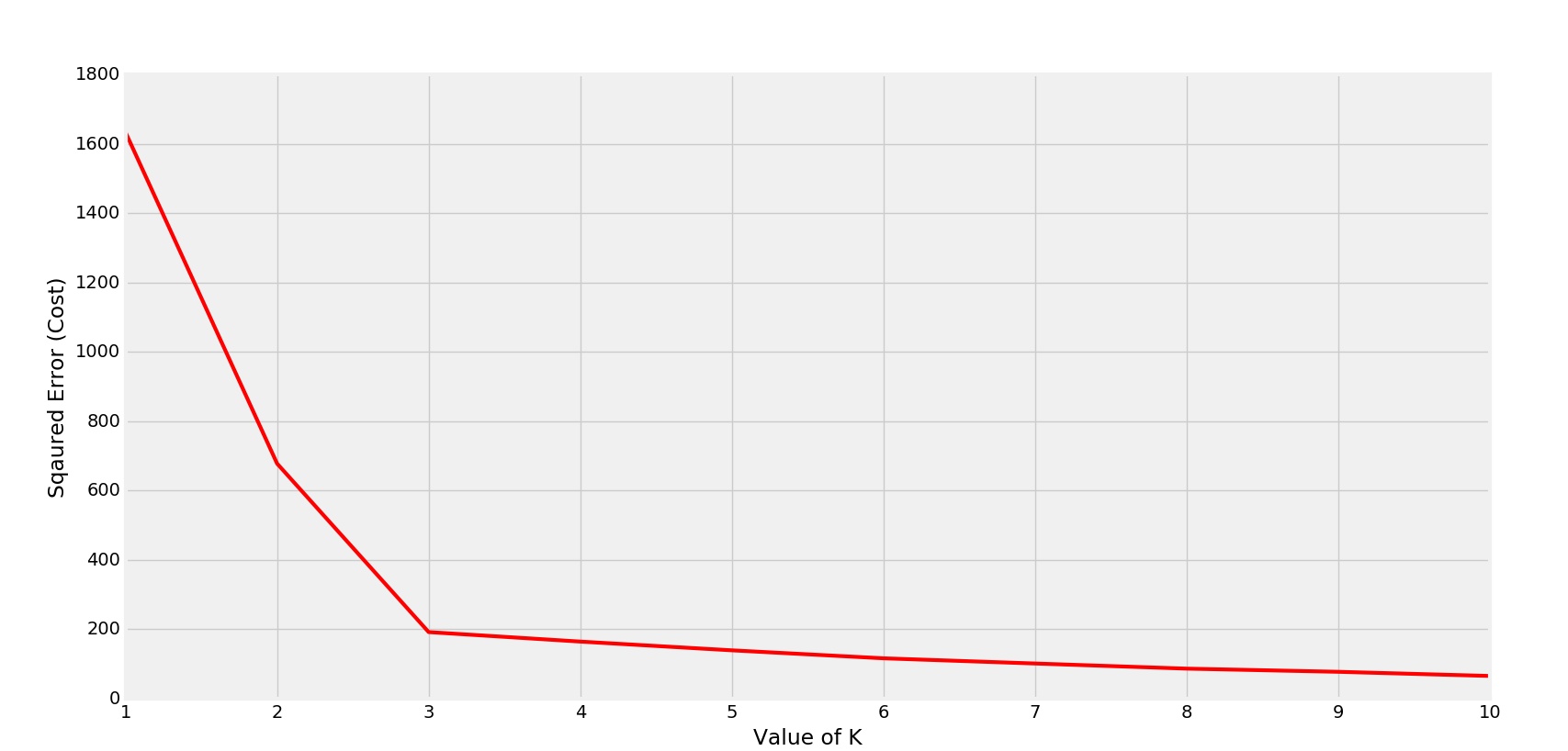
График соответствующей стоимости

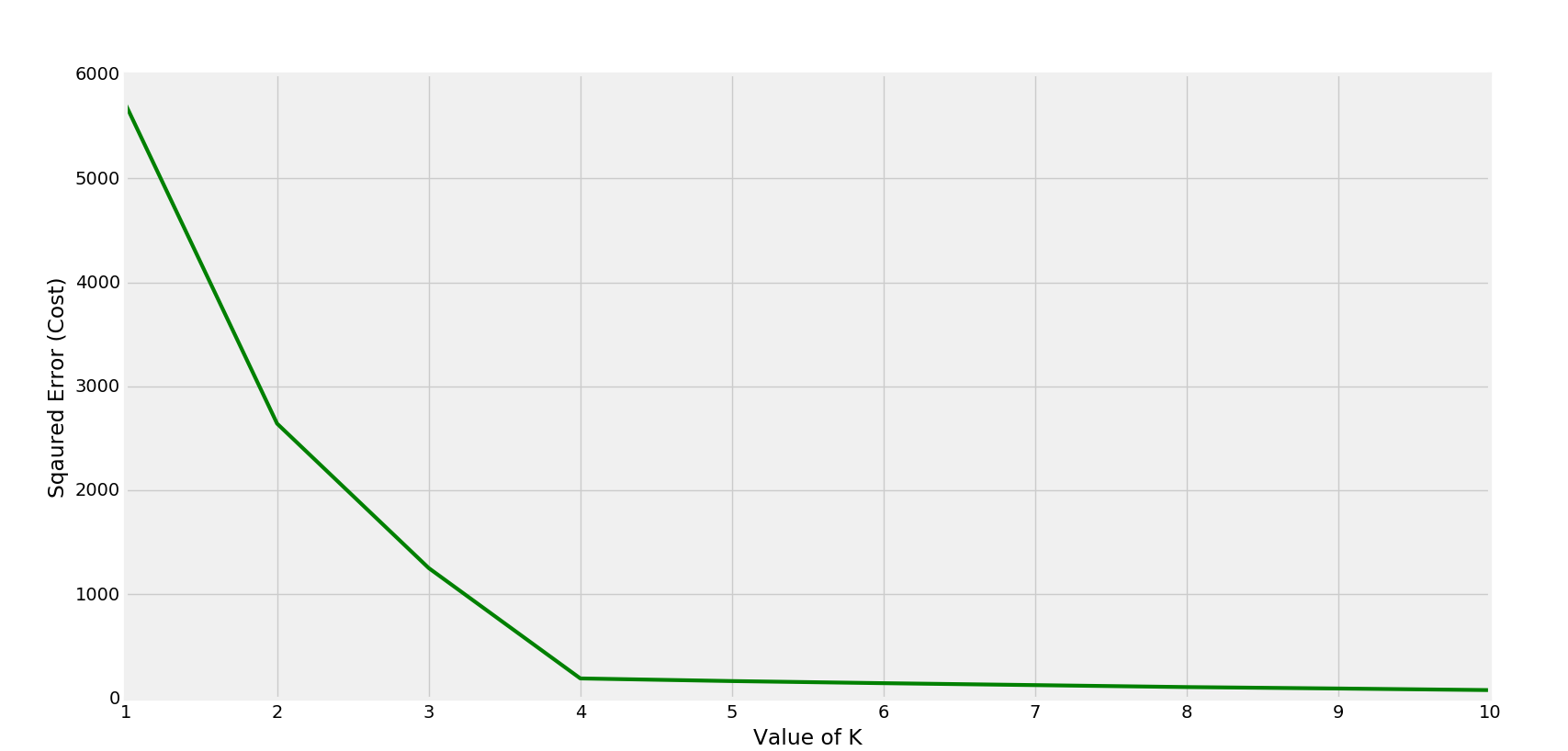
Колено формируется при К = 4

В этом случае оптимальным значением k будет 4. (Наблюдается по разнесенным точкам).

Ниже представлена реализация Python:

import matplotlib.pyplot as plt 
from matplotlib import style
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs
  
style.use("fivethirtyeight")
  
# make_blobs() is used to generate sample points
# around c centers (randomly chosen)
X, y = make_blobs(n_samples = 100, centers = 4, 
                cluster_std = 1, n_features = 2)
                  
plt.scatter(X[:, 0], X[:, 1], s = 30, color ="b")
  
# label the axes
plt.xlabel("X")
plt.ylabel("Y")
  
plt.show()
plt.clf() # clear the figure

Выход: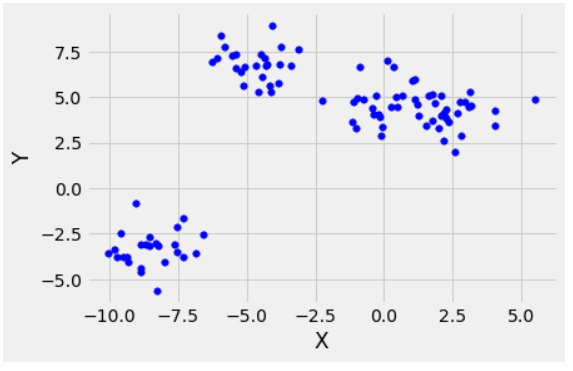

 cost = []
 for i in range ( 1 , 11 ):
    KM = KMeans(n_clusters = i, max_iter = 500 )
    KM.fit(X)
     
    # calculates squared error
    # for the clustered points
    cost.append(KM.inertia_)
 
# plot the cost against K values
 plt.plot( range ( 1 , 11 ), cost, color = 'g' , linewidth = '3' )
 plt.xlabel( "Value of K" )
 plt.ylabel( "Sqaured Error (Cost)" )
 plt.show() # clear the plot
 
# the point of the elbow is the
 # most optimal value for choosing k

Выход:

Python Машинное обучение

ML | Определите оптимальное значение K в кластеризации K-средних

РЕКОМЕНДУЕМЫЕ СТАТЬИ