ML | Операции линейной алгебры

Принципы линейной алгебры имеют решающее значение для понимания концепции машинного обучения, а также глубокого обучения, даже многие идеи борются за создание точной математической модели, линейная алгебра продолжает оставаться важным инструментом для их исследования. Алгебра дает вам лучшее понимание того, как алгоритмы на самом деле работают под капотом, поэтому разработчик может сделать лучший выбор, и невозможно избежать изучения некоторых из этих методов, если кто-то хочет стать профессионалом в области машинного обучения или глубокого обучения.

Что такое линейная алгебра?
Это раздел математики, который позволяет кратко определять и выполнять операции с многомерными координатами и взаимодействиями плоскостей. Линейная алгебра - это расширение алгебры до неопределенного числа измерений. Линейная алгебра сосредоточена на системах линейных уравнений. Это непрерывный тип математики, который применим в науке и технике, поскольку помогает моделировать и эффективно моделировать природные явления.

Прежде чем перейти к концепциям линейной алгебры, мы должны понять следующие свойства:

• Ассоциативное свойство: это свойство в математике, которое гласит, что если a , b и c являются математическими объектами, то a + (b + c) = (a + b) + c, в котором + является бинарной операцией.
• Коммутативное свойство: это свойство в математике, которое гласит, что если a и b являются математическими объектами, то a + b = b + a, в котором + является бинарной операцией.
• Распределительное свойство: это свойство в математике, которое утверждает, что если a , b и c являются математическими объектами, то a * (b + c) = (a * b) + (a * c), в котором * и + являются бинарными операторами.

Ниже приведены некоторые концепции линейной алгебры, которые в основном используются при реализации машинного обучения:

• Скаляр: это физическая величина, описываемая одним элементом. Она имеет только величину, а не направление. По сути, скаляр - это просто одно число.

   Пример: 
  17 и 256

• Вектор: это геометрический объект, имеющий как величину, так и направление, это упорядоченный числовой массив, который всегда находится в строке или столбце. Вектор имеет только один индекс, который может ссылаться на конкретное значение в векторе.
  
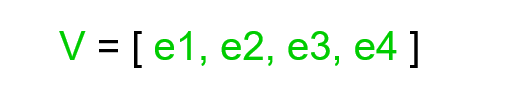
  Здесь V - вектор, в котором e1 , e2 , e3 и e4 - его элементы, а V [2] - это e3 .
  
  
  
  

   Пример: 
  [2, 3, 4] и [34, 53]

  Операции:

  • Скалярно-векторное умножение:

     p = [e1, e2, e3]

    Произведение скаляра на вектор дает следующий результат:

     p * 2 = [2 * e1, 2 * e2, 2 * e3]

    когда скаляр 2 умножается на вектор p, тогда все элементы вектора p умножаются на этот скаляр. Эта операция обладает коммутативным свойством.

     Пример:
    х = [1, 2]
    х * 4 = [4, 8]

• Матрица: это упорядоченный двумерный массив чисел, символов или выражений, расположенных в строках и столбцах. У него два индекса: первый указывает на строку, а второй - на столбец. Матрица может иметь несколько строк и столбцов.
  
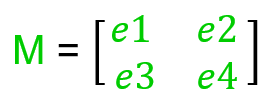
  Выше M - это двумерная матрица, имеющая в качестве элементов e1 , e2 , e3 и e4 , а M [1] [0] - это e3 .

   Пример:
  2 3 6 и 56 12 
  4 5 8 45 78
             34 67

  Матрица, в которой элементы левой диагонали равны 1, а другие элементы - 0, является матрицей идентичности .

   Пример:
  1 0 
  0 1 - это 2D-матрица идентичности.
  
  1 0 0
  0 1 0
  0 0 1 - это 3D-матрица идентичности.

  Операции:

  • Скалярно-матричное умножение:

    р = е1 е2 
        e3 e4
    а - скаляр.
    р * а = (а * е1) (а * е2)
            (а * е3) (а * е4)

    Когда скаляр a умножается на матрицу p, тогда все элементы матрицы p умножаются на этот скаляр. Умножение скалярных матриц ассоциативно, дистрибутивно и коммутативно.

    
    
    
    

     Пример:
    х = 1 2 3
        4 5 6
    х * 4 = 4 8 12
            16 20 24

  • Векторное матричное умножение:

    р = е1 е2
        e3 e4
        e5 e6
    д = а
        б

    Умножение матрицы p на вектор q дает следующий продукт:

    p * q = (e1 * a) + (e2 * b)
            (e3 * a) + (e4 * b)
            (e5 * a) + (e6 * b)

    Количество строк матрицы должно быть равно количеству элементов вектора, тогда только их можно умножать. Умножение вектор-матрица ассоциативно и дистрибутивно, но не коммутативно.

     Пример:
    m = 1 2 и n = 1
        3 4 2 
        5 6
    тогда m * n = 5
                 11
                 17

  • Матрица-Матрица Дополнение:

    m1 = ab и m2 = pqcdrs

    Для добавления матриц строки и столбцы матриц должны быть равны. Сложение матриц m1 и m2 дает следующий результат:

    m1 + m2 = (a + p) (b + q)
              (с + г) (д + с)

    Каждый элемент первой матрицы добавляется к соответствующему элементу другой матрицы, оба имеют одинаковое значение строки и столбца. Матрица-матричное сложение бывает ассоциативным, дистрибутивным и коммутативным.

     Пример:
    1 2 5 5 6 7
    2 1 + 5 5 = 7 6
    1 2 5 5 6 7

  • Матрица-матричное вычитание:

    m1 = ab и m2 = pqcdrs

    Для вычитания матриц строки и столбцы матриц должны быть равны. Вычитание между матрицами m1 и m2 дает следующий результат:

    m1 - m2 = (a - p) (b - q)
              (с - г) (д - с)

    Каждый элемент первой матрицы вычитается, а соответствующий элемент другой матрицы имеет одинаковое значение строки и столбца. Матрица-матричное сложение бывает ассоциативным, дистрибутивным и коммутативным.

     Пример:
    1 2 5 5-4-3
    2 1 - 5 5 = -3-4
    1 2 5 5-4-3

  • Матрица-матричное умножение:

    m1 = ab и m2 = pqcdrs

    Чтобы перемножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк во второй матрице, произведение матрицы m1 и m2 приведено ниже:

    m1 * m2 = ((a * p) + (b * r)) ((a * q) + (b * s))  
              ((c * p) + (d * r)) ((c * q) + (d * s))

    Умножение матрицы на матрицу является ассоциативным и дистрибутивным, но не коммутативным.

     Пример:
    1 3 2 1 3 11 10
    4 0 1 * 0 1 = 9 14
            5 2
    1 3 2 1 11
    4 0 1 * 0 = 9 
            5 
    1 3 2 3 10
    4 0 1 * 1 = 14
            2

    Пусть х1, х2 и х3 матрицы таким образом, что X1 имеет число строк и б число столбцов и х2 имеет Ь число строк и С числом столбцов и x3 является произведением x1 и x2 так, х3 будет иметь ряд строк и c количество столбцов. х1 * х2 = х3 , в котором х3 имеет строки и столбцы гр.

  • Транспонировать:
    Транспонирование матрицы создает новую матрицу, в которой строки становятся столбцами, а столбцы становятся строками исходной матрицы.

     m = ab
        CD
    Транспонировать (м) = acbd

    Если A - это матрица, а B - это транспонированная матрица A, тогда транспонированная матрица B - это исходная матрица A.
    B = Транспонирование (A), затем Транспонирование (B) = Транспонирование (Транспонирование (A)) = A

     Пример:
    х = 1 2 3
    Транспонирование матрицы x равно 1
                             2 
                             3

    Транспонирование матрицы m * n даст матрицу n * m .

  • Обратный:
    Матрица, обратная матрице, - это матрица, при умножении на исходную матрицу в качестве продукта получается матрица идентичности. Если m - матрица, а n - матрица, обратная m , то m * n = I , в котором я представляю матрицу идентичности.

     Пример:
    m = 4 7 и обратное (m) = 0,6 -0,7  
        2 6 -0,2 0,4
    4 7 * 0,6 -0,7 = 1 0 
    2 6 -0,2 0,4 0 1

• Тензор: это алгебраический объект, представляющий линейное отображение алгебраических объектов из одного набора в другой. На самом деле это трехмерный массив чисел с переменным числом осей, расположенный на регулярной сетке. Тензор имеет три индекса: первый индекс указывает на строку, второй индекс указывает на столбец, а третий индекс указывает на ось.

  

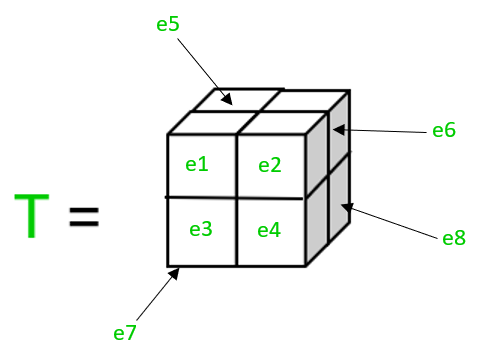
  Здесь тензор T имеет 8 элементов e1 , e2 , e3 , e4 , e5 , e6 , e7 и e8, в которых T [0] [3] [1] равно e8 .