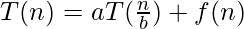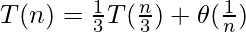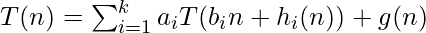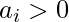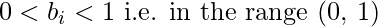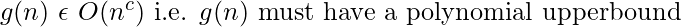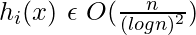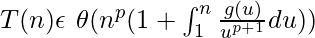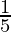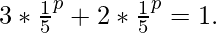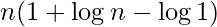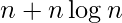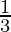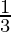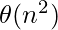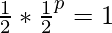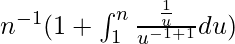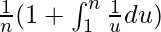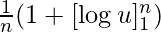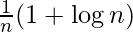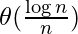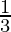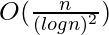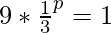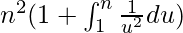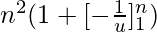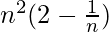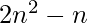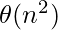Метод Акра-Бацци для нахождения временных сложностей

Теорема Мастера - популярный метод решения повторяющихся временных сложностей в форме:

С ограничениями на a, b и f(n). Форма рекуррентного отношения ограничивает применимость теоремы Мастера. Ниже приведены три повторения, которые нельзя решить напрямую с помощью теоремы мастера:

Метод Акра-Бацци : в этой статье исследуется другой метод решения таких повторений, разработанный Мохаммадом Акрой и Луай Баззи в 1996 году . Метод Акра-Бацци можно применять к рецидивам следующей формы:

куда, 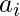а также 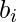такие константы, что:

Далее найдите такое p, что

затем

Примеры
Рассмотрим три рекуррентности, рассмотренные выше, и решим их методом:

Пример 1.

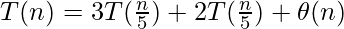
Здесь

1. a₁ = 3
2. b₁ = 
3. a₂ = 2
4. b₂ = 
5. b₁ and b₂ are in the range (0, 1)
6. g(n) = heta(n) which is O(n^c), here c can be 1.

В этой задаче h ₁ (n) и h ₂ (n) отсутствуют.
Здесь p=1 удовлетворяет

Окончательно,

=> 

=> 

=>

=>

Пример 2.

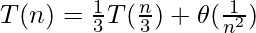
Здесь

1. a = 
2. b = 
3. g(n) = 
4. b is in the range (0, 1)
5. g(n) = heta(n^2) which is in O(n^c), here c can be 1.

В этой задаче h(n) отсутствует.
Здесь p= – 1 удовлетворяет

Окончательно,

=> 

=> 

=> 

=> 

=> 

Пример 3.

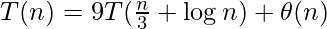
Здесь

1. a = 9
2. b = 
3. g(n) = heta(n)
4. b is in the range(0, 1)
5. g(n) =  which is O(n^c), here c can be 1.
6. h(n) =   which is 

Здесь p=2 удовлетворяет

Окончательно,

=> 

=> 

=> 

=> 

=> 

=> 

Преимущества:

• Работает для многих алгоритмов «разделяй и властвуй».
• Имеет меньшее ограничение на формат повторения, чем Теорема Мастера.
• p можно рассчитать с помощью численных методов для сложных рекуррентных соотношений.

Недостатки:

• Не работает, когда рост g(n) не является ограниченным полиномом. Например, g(N) = 2 ^N .
• Не работает с потолочными и напольными функциями.