Матрица совпадения уровней серого в MATLAB

Опубликовано: 18 Февраля, 2023

Использование текстуры для определения областей интереса на изображении является важной характеристикой. Одним из первых подходов Харалика и др. к извлечению признаков текстур были матрицы совпадения уровней серого (GLCM) в 1973 году. С тех пор он широко использовался в ряде приложений для анализа текстур и продолжает оставаться важным метод выделения признаков при анализе текстуры. Харалик использовал GLCM для выделения четырнадцати признаков для описания текстуры. В приложениях CBIR Даченг и др. использовали трехмерные матрицы совпадений. Для сопоставления и распознавания объектов Ковалев и Петров использовали специальные многомерные матрицы совпадений. Методы кластеризации используют впервые продемонстрированный многомерный текстурный анализ. Матрицы совпадения и извлечение ими дополнительных признаков из n-мерных евклидовых пространств являются целями этой работы, которая распространяет концепцию на эти пространства. В приложениях CBIR новые функции оказались полезными.

Матрица совпадения уровней серого:

Пространственные отношения между соседними или соседними пикселями обеспечиваются GLCM. Мы измерим некоторые особенности текстуры из этой матрицы GLCM. Метод статистического анализа текстуры второго порядка называется GLCM. Он измеряет частоту, с которой пиксели в заданном направлении и на расстоянии d присутствуют в изображении, и исследует пространственные отношения между ними. Матрица пространственной зависимости в оттенках серого — это другое название матрицы одновременности в оттенках серого. Выяснив, как часто два пикселя с одинаковым значением интенсивности оттенков серого — i и j — встречаются горизонтально рядом друг с другом, матрица серого генерирует GLCM.

Синтаксис:

glcms = graycomatrix(I)
glcms = graycomatrix(I,Name,Value)
[glcms,SI] = graycomatrix(___)

glcms — из изображения I матрица серого (I) генерирует матрицу совпадения уровней серого (GLCM), которая также известна как матрица пространственной зависимости уровня серого.
glcms — в зависимости от значений необязательных аргументов пары «имя-значение» матрица серого (I, Name, Value) возвращает одну или несколько матриц совпадения уровней серого.
[glcms,SI] — Масштабированное изображение, SI, используемое для расчета матрицы совпадения уровней серого, возвращается матрицей серого (___).

Рассчитать матрицу GLCM:

Используйте функцию Graycomatrix, чтобы построить GLCM. Функция определяет, как часто пиксель со значением интенсивности (уровня серого) I встречается в определенном пространственном отношении к пикселю со значением j для создания матрицы совместного появления в оттенках серого (GLCM). Исследуемый пиксель и пиксель непосредственно справа от него (смежный по горизонтали) являются определениями пространственного отношения по умолчанию, но вы можете указать другие пространственные отношения между двумя пикселями. Количество раз, когда пиксель входного изображения со значением I встречался в заданном пространственном отношении с пикселем со значением j, просто добавляется для каждого элемента (i,j) в конечном glcm.

Количество затемненных уровней в изображении определяет размер GLCM. Graycomatrix использует масштабирование, чтобы уменьшить количество значений интенсивности в изображении до восьми по умолчанию. Однако вы можете управлять этим масштабированием уровней серого, используя параметры NumLevels и GrayLimits.

Пространственное распределение уровней серого в текстурном изображении можно узнать из матрицы совпадения уровней серого. Например, текстура является грубой по отношению к указанному смещению, если большинство записей в GLCM сосредоточено по диагонали. GLCM также можно использовать для расчета ряда статистических показателей.

Пример 1:

Matlab

clear all
% GLCM MATRIX
  
X=[6 7 8 7 8; 5 6 7 8 9; 7 7 4 4 7; 3 4 3 4 3; 2 9 2 9 9];
% Amount of steps between two pixels
Displacement = 1; 
  
% Amount of Quantization Level
NumQuantLevels = 9; 
glcm = zeros([NumQuantLevels,NumQuantLevels]); 
  
% PRREALOCATING THE GLCM MATRIX
  
for i = 1:size(X,1)
    for j = 1 :size(X,2)-1
        glcm(X(i,j),X(i,j+1))=glcm(X(i,j),X(i,j+1))+1; 
        % INCREASE BY 1 % 
    end
  
end

Выход:

Объяснение:

Подсчитывается, сколько раз появляется пиксель и соседний с ним пиксель. Смещение равно 1, но при необходимости его можно увеличить. Движение пикселей здесь происходит в правильном направлении. Уровень квантования установлен на 9, потому что каждый пиксель в матрице X имеет максимальное значение 9. В предыдущем примере, например, пиксель 6 и его сосед 7 встречаются в матрице X шесть раз, и матрица GLCM обновляет их в позиции (6,7) как 2.

Пример 2:

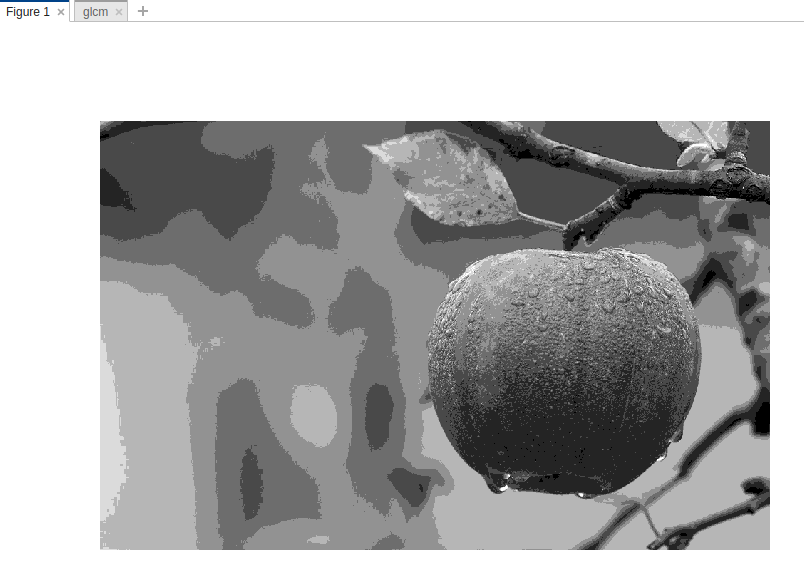
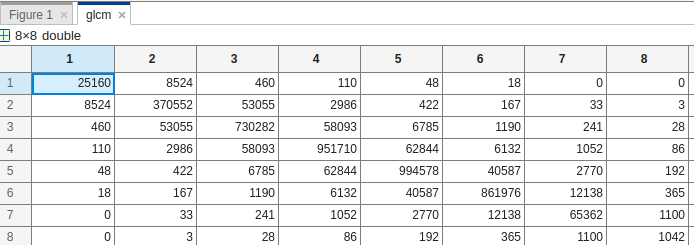
Matlab

clear clc
% GLCM MATRIX
I = imread("apple1.png");
imshow(I)
[glcm,SI] = graycomatrix(I,"Offset",[2 0],"Symmetric",true);
glcm; 
imshow(rescale(SI))

Выход:

Technical Scripter Picked

Матрица совпадения уровней серого в MATLAB