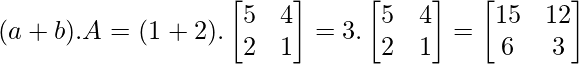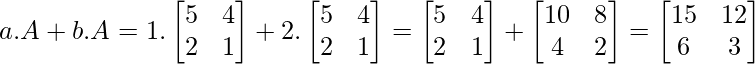Математические операции над матрицами | 12 класс по математике

Матрица - это прямоугольное расположение чисел, символов или выражений, упорядоченное по строкам и столбцам. Матрица может содержать m строк и n столбцов, тогда она называется матрицей m × n.

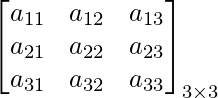
Матрицы записываются в квадратных скобках, где горизонтальные линии называются строками, например, в приведенной выше матрице - a ₁₁ , a ₁₂ , a ₁₃ .

Вертикальные линии называются столбцами, например - ₁₁ , ₂₁ , ₃₁ . Размер матрицы определяется количеством строк и столбцов.

Равенство матриц

Две матрицы «А» и «В» называются равными, если они удовлетворяют следующим трем условиям;

• Если количество строк в матрице «A» и матрице «B» одинаковое.
• Если количество столбцов в матрице «A» и матрице «B» одинаковое.
• Соответствующие элементы в матрице «A» и матрице «B» находятся в одной позиции.
  

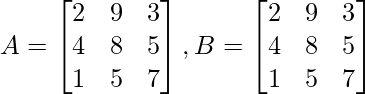
Здесь матрицы «A» и «B» равны, поскольку они удовлетворяют всем трем вышеупомянутым условиям.

Проблема: найти значение «x» и «y», если следующие матрицы равны?

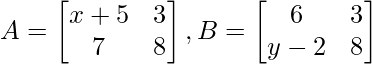
Решение:

On equating the corresponding elements we can the value of ‘x’ and ‘y’

• x + 5 = 6
  x = 6 – 5
  x = 1
• 7 = y – 2
  7 + 2 = y
  y = 9

Добавление матриц

В матрице добавление матриц - это сложение двух матриц путем сложения соответствующих элементов вместе.
Условием сложения двух матриц является:
Две матрицы должны иметь одинаковый порядок или размер, то есть количество строк должно быть равно количеству столбцов.

Пример:

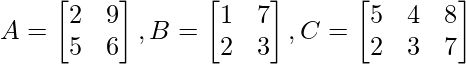
• Здесь могут быть добавлены матрицы 'A' и 'B', поскольку они обе находятся в порядке 2 × 2,
  

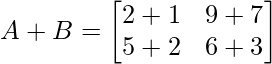
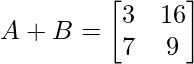
• Кроме того, нельзя добавить «A» + «C», поскольку они находятся в другом порядке, матрица «A» имеет порядок 2 × 2, а матрица «C» имеет порядок 2 × 3.

Вычитание матриц

В матрице вычитание матриц - это функция вычитания двух матриц путем вычитания соответствующих элементов вместе.
Условие вычитания двух матриц:
Две матрицы должны иметь одинаковый порядок или размер, то есть количество строк должно быть равно количеству столбцов.

Пример:

Здесь порядок матриц A и B 2 × 2,
Вычитание соответствующих элементов

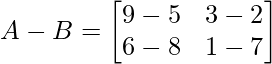
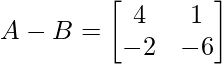
Умножение матриц на скаляры

При скалярном умножении каждый элемент матрицы умножается на скаляр. Здесь мы называем скаляр действительными числами.

Свойства умножения матриц на скаляры

Размерное свойство

Если мы умножим матрицу на скаляр, размерность матрицы не изменится, она останется такой же, как это объясняется в следующем примере,

В приведенном выше примере, когда мы умножили матрицу размера 2 × 2 на скаляр 2, то результирующая матрица также имеет размер 2 × 2.

Коммутативная собственность

Изменение порядка умножения матрицы не меняет результата. При умножении матрицы на скаляр порядок, в котором множители располагаются при умножении, не влияет на результат.
Например: пусть 'a' будет скаляром, а 'A' будет матрицей
Под этим свойством мы понимаем, что

аА = Аа

Пример:

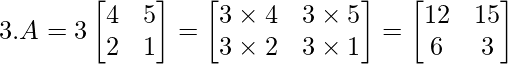
3.A = A.3

Ассоциативное свойство

Умножение матрицы является ассоциативным, то есть при умножении матрицы на два скаляра, порядок умножения скаляров и матрицы не изменится в результате. Пусть 'a' и 'b' - скаляр, а 'X' - матрица, тогда

(aX) .b = a. (Xb)

Пример: a = 2, b = 7. и X - любая матрица 2 × 2.

(aX) .b = a. (Xb)

Распределительное свойство

Распределительное свойство матриц гласит, что при умножении скаляра на матрицы «A» и «B» и включении в умножение также применяются другие арифметические операции, такие как сложение или вычитание. Мы используем свойство распределенности, чтобы прояснить задачи, в которых одним из факторов при умножении скалярных матриц является сложение или вычитание.

Пример 1. Пусть «a» - скаляр, а «A» и «B» - матрицы.
а. (А + В) = аА + аБ

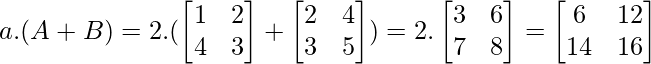
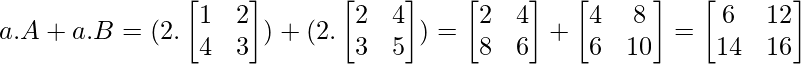
а. (А + В) = аА + аБ

Пример 2: Если одна из операций умножения - это сложение скаляров, то свойство распределения определяется выражением
Пусть «a» и «b» скалярны, а «A» - матрица.
(a + b) .A = aA + bA