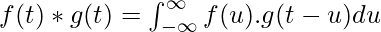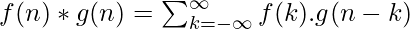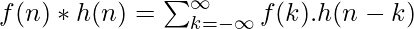Линейная свертка с использованием C и MATLAB

Ключевой концепцией, которую часто представляют тем, кто занимается разработкой электроники, является линейная свертка. Это важнейший компонент цифровой обработки сигналов и сигналов и систем. Помня об общем интересе и академических последствиях, эта статья знакомит с концепцией и ее приложениями, а также реализует ее с использованием C и MATLAB.

Свертка: Если говорить чисто математически, свертка — это процесс, с помощью которого можно вычислить перекрытие двух графиков. На самом деле свертка также интерпретируется как площадь, разделяемая двумя графами во времени. Метафорически это смесь двух функций, когда одна проходит над другой. Таким образом, для двух функций F(n) и G(n) их свертка выражается и задается следующим математическим выражением:

or

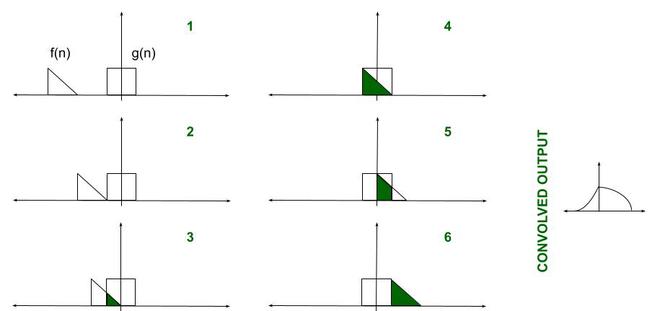
Итак, как бы интуитивно это ни выглядело, мы должны учитывать ВРЕМЯ. Свертка включает функции, которые смешиваются во времени. Это вводится в выражение с использованием временного сдвига, т. е. g(tu) есть g(t), сдвинутое вправо на 'u' раз). Кроме того, важно, как мы характеризуем это время. Прежде чем двигаться дальше, давайте скомпилируем необходимые предварительные условия:

• Функции: Математически мы рассматриваем функции или графики. Однако важно отметить, что практическим эквивалентом здесь является Сигнал. Мы имеем дело со сверткой 2-х сигналов.
• LTI-системы: линейные стационарные системы — это системы или процессы, производящие линейные и стационарные выходные данные, т. е. выходные данные удовлетворяют линейности (правило суперпозиции) и не меняются со временем. Свертка — это отношение между входом и выходом системы LTI.
• Импульсная характеристика: Импульсная характеристика — это то, что вы обычно получаете, если рассматриваемая система подвергается воздействию кратковременного сигнала во временной области. Различные системы LTI имеют разные импульсные характеристики.
• Система времени: мы можем использовать сигналы непрерывного времени или сигналы дискретного времени. Предполагается, что разница известна и понятна читателям. Свертку можно определить для сигналов CT и DT.

Линейная свертка: Линейная свертка — это средство, с помощью которого можно связать выходные и входные данные системы LTI с учетом импульсной характеристики системы. Ясно, что требуется свертка входного сигнала с импульсной характеристикой системы. Используя выражение ранее, можно составить следующее уравнение:

Причина, по которой выражение суммируется бесконечное число раз, состоит в том, чтобы гарантировать, что вероятность перекрытия двух функций равна 1. Импульсная характеристика бесконечно сдвигается во времени, так что в течение некоторого промежутка времени две функции обязательно перекрываются. Может показаться, что со стороны программиста было бы небрежно запускать бесконечный цикл — код может продолжать выполняться до тех пор, пока две функции не перекрываются.

Решение заключается в том, что используются системы LTI. Поскольку функции не меняют свои значения/форму с течением времени (неизменны во времени), их можно просто сдвинуть ближе друг к другу. Помните, что требуется только вывод, и не важно, когда он будет получен. Все ручные расчеты также основаны на той же идее.

Объяснение: Вот один метод, который можно использовать при расчете выходных данных:

• Возьмите входной сигнал и импульсную характеристику как две отдельные однострочные матрицы.
• Первый элемент импульсной характеристики умножается на каждый элемент входного сигнала. Этот результат сохраняется.
• Второй элемент импульсной характеристики умножается на каждый элемент входного сигнала. Результат сдвигается на один шаг вправо и сохраняется.
• Вышеуказанные два шага выполняются для оставшихся элементов импульсной характеристики.
• Как только все элементы будут перемножены, выровняйте все результаты друг под другом. См. рисунок ниже.
• Вертикально добавьте все элементы в каждом столбце.
• Результирующая однострочная матрица является свернутым выходом.

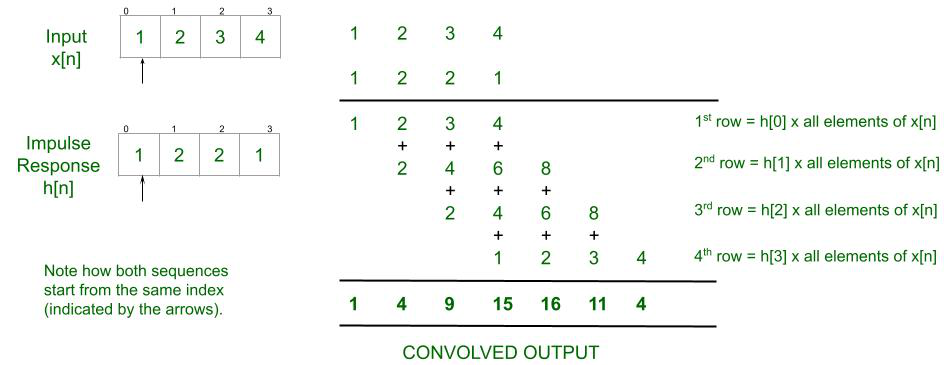
Подход:

• Получите входной сигнал и импульсную характеристику как два отдельных массива.
• Получите последовательность временных индексов. Последовательность временных индексов — это способ, с помощью которого MATLAB информируется о том, когда запускаются наши функции. По умолчанию он начинается с 0, т.е. [0 1 2 3 ……..]. Однако вторая последовательность или импульсная характеристика не обязательно должны начинаться одновременно. Можно отложить или начать раньше. Если он вводится на секунду раньше, то его последовательность временных индексов следует вводить как [-1 0 1 2 …….].
• Используйте пользовательские функции. Функция findconv() определяет, как вычисляется длина вывода. Определите « ny » как длину нашей оси X в выходных данных. Ранее он был определен как массив, начинающийся с ' nybegin ' и заканчивающийся ' nyend '. Функция calconv() упоминается в findconv() и вычисляет фактический результат последовательно, принимая разные значения k и n, используя 2 различных цикла for.
• Для каждого значения n сумма выходов рассчитывается путем взятия разных значений X(k) на каждой итерации.
• Этот результат сохраняется в массиве – y(n).
• Постройте результат. Функция стебель() используется при построении графика из-за того, что ввод по своей природе является ДИСКРЕТНЫМ. Если бы нужно было построить вывод в непрерывном времени, не было бы никакого смысла использовать функцию стебель(), так как это создавало бы впечатление, что вывод является выборочным. Рекомендуется использовать plot(x_axis, y_axis) при построении непрерывных значений.
• Примечание. НЕ изменяйте длину последовательности временных индексов, а также 1-й и 2-й последовательностей. Stem() возвращает ошибку, указывающую на то, что он не может установить длину оси X в выходных данных.

Ниже приведена программа Matlab для реализации описанного выше подхода:

Ввод (любой произвольный набор чисел):

>> Enter the 1st Sequence: [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17]
>> Enter the Time Index sequence: [0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16]
>> Enter the second sequence: [1 2 2 1 4 5 2 2 1 1 4 5 2 2 1 2 2]
>> Enter the Time Index sequence: [0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16]

Выход:

>> Columns 1 through 17
    1     4     9    15    25    40    57    76    96   117   142   172   204   238   273   310   349

>> Columns 18 through 33

   370   372   372   388   349   288   276   262   264   265   211   135   108    79    66    34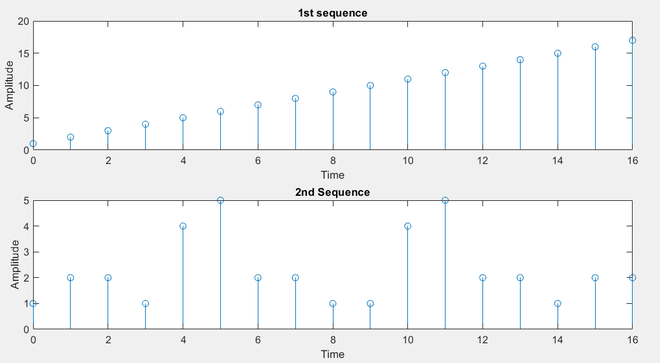

Это входные последовательности. Обратите внимание, что это последовательности дискретного времени.

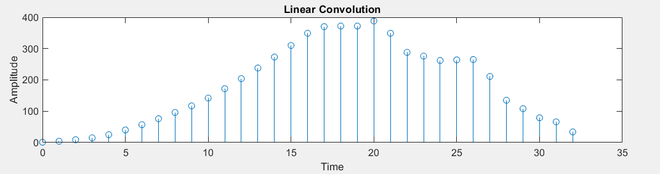
Выход. Это также Дискретно во времени.

Примечание. Читателям рекомендуется попытаться сделать то же самое, используя сигналы с непрерывным временем. В этих случаях вход принимается как заранее определенный непрерывный сигнал, такой как y = sin x. Кроме того, используйте график (ось x, ось y), а не стебель (ось x, ось y).

Ниже приведена программа на C для реализации описанного выше подхода:

Вход:

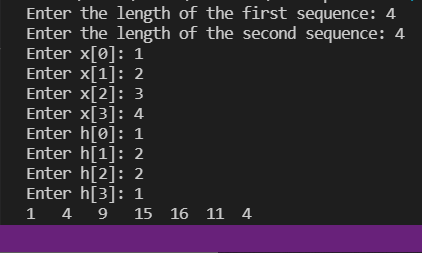
Enter the length of the first sequence: 4
Enter the length of the second sequence: 4
Enter x[0]: 1
Enter x[1]: 2
Enter x[2]: 3
Enter x[3]: 4
Enter h[0]: 1
Enter h[1]: 2
Enter h[2]: 2
Enter h[3]: 1

Выход:

1    4    9    15    16    11    4