LCA в дереве с использованием техники бинарного подъема

Опубликовано: 14 Января, 2022

Учитывая двоичное дерево, задача состоит в том, чтобы найти наименьшего общего предка данных двух узлов в дереве.
Пусть G - дерево, тогда LCA двух узлов u и v определяется как узел w в дереве, который является предком как u, так и v и наиболее удален от корневого узла. Если один узел является предком другого, чем этот конкретный узел - это LCA этих двух узлов.
Пример:

Input: 

Output: 
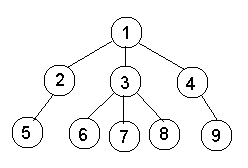
The LCA of 6 and 9 is 1. 
The LCA of 5 and 9 is 1. 
The LCA of 6 and 8 is 3. 
The LCA of 6 and 1 is 1. 
 

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: в статье описывается подход, известный как двоичный подъем, чтобы найти наименьшего общего предка двух узлов в дереве. Для решения проблемы LCA может быть много подходов. Мы обсуждаем технику бинарного лифтинга, остальные можно прочитать здесь и здесь.
Двоичный подъем - это подход динамического программирования, при котором мы предварительно вычисляем массив memo [1, n] [1, log (n)], где memo [i] [j] содержит 2 ^ j-го предка узла i. Для вычисления значений memo [] [] может использоваться следующая рекурсия

memo[i][j] = parent[i] if j = 0 and 
memo[i][j] = memo[memo[i][j – 1]][j – 1] if j > 0. 

Сначала мы проверяем, является ли узел предком другого или нет, и если один узел является предком другого, то это LCA этих двух узлов, в противном случае мы находим узел, который не является общим предком как u, так и v и является самым высоким ( то есть такой узел x, что x не является общим предком u и v, но memo [x] [0] является) в дереве. Найдя такой узел (пусть это будет x), мы печатаем первого предка x, то есть memo [x] [0], который будет требуемым LCA.

Below is the implementation of the above approach: 

C++

// C++ implementation of the approach 
#include <bits/stdc++.h> 
using namespace std; 
  
// Pre-processing to calculate values of memo[][] 
void dfs(int u, int p, int **memo, int *lev, int log, vector<int> *g) 
{ 
    // Using recursion formula to calculate 
    // the values of memo[][] 
    memo[u][0] = p; 
    for (int i = 1; i <= log; i++) 
        memo[u][i] = memo[memo[u][i - 1]][i - 1]; 
    for (int v : g[u]) 
    { 
        if (v != p) 
        { 
            lev[v] = lev[u] + 1; 
            dfs(v, u, memo, lev, log, g); 
        } 
    } 
} 
  
// Function to return the LCA of nodes u and v 
int lca(int u, int v, int log, int *lev, int **memo) 
{ 
    // The node which is present farthest 
    // from the root node is taken as u 
    // If v is farther from root node 
    // then swap the two 
    if (lev[u] < lev[v]) 
        swap(u, v); 
  
    // Finding the ancestor of u 
    // which is at same level as v 
    for (int i = log; i >= 0; i--) 
        if ((lev[u] - pow(2, i)) >= lev[v]) 
            u = memo[u][i]; 
  
    // If v is the ancestor of u 
    // then v is the LCA of u and v 
    if (u == v) 
        return u; 
  
    // Finding the node closest to the root which is 
    // not the common ancestor of u and v i.e. a node 
    // x such that x is not the common ancestor of u 
    // and v but memo[x][0] is 
    for (int i = log; i >= 0; i--) 
    { 
        if (memo[u][i] != memo[v][i]) 
        { 
            u = memo[u][i]; 
            v = memo[v][i]; 
        } 
    } 
  
    // Returning the first ancestor 
    // of above found node 
    return memo[u][0]; 
} 
  
// Driver Code 
int main() 
{ 
    // Number of nodes 
    int n = 9; 
  
    // vector to store tree 
    vector<int> g[n + 1]; 
  
    int log = (int)ceil(log2(n)); 
    int **memo = new int *[n + 1]; 
    for (int i = 0; i < n + 1; i++) 
        memo[i] = new int[log + 1]; 
  
    // Stores the level of each node 
    int *lev = new int[n + 1]; 
  
    // Initialising memo values with -1 
    for (int i = 0; i <= n; i++) 
        memset(memo[i], -1, sizeof memo[i]); 
  
    // Add edges 
    g[1].push_back(2); 
    g[2].push_back(1); 
    g[1].push_back(3); 
    g[3].push_back(1); 
    g[1].push_back(4); 
    g[4].push_back(1); 
    g[2].push_back(5); 
    g[5].push_back(2); 
    g[3].push_back(6); 
    g[6].push_back(3); 
    g[3].push_back(7); 
    g[7].push_back(3); 
    g[3].push_back(8); 
    g[8].push_back(3); 
    g[4].push_back(9); 
    g[9].push_back(4); 
    dfs(1, 1, memo, lev, log, g); 
    cout << "The LCA of 6 and 9 is " << lca(6, 9, log, lev, memo) << endl; 
    cout << "The LCA of 5 and 9 is " << lca(5, 9, log, lev, memo) << endl; 
    cout << "The LCA of 6 and 8 is " << lca(6, 8, log, lev, memo) << endl; 
    cout << "The LCA of 6 and 1 is " << lca(6, 1, log, lev, memo) << endl; 
  
    return 0; 
} 
  
// This code is contributed by 
// sanjeev2552 

Java

// Java implementation of the approach 
import java.util.*; 
public class GFG { 
  
    // ArrayList to store tree 
    static ArrayList<Integer> g[]; 
    static int memo[][], lev[], log; 
  
    // Pre-processing to calculate values of memo[][] 
    static void dfs(int u, int p) 
    { 
  
        // Using recursion formula to calculate 
        // the values of memo[][] 
        memo[u][0] = p; 
        for (int i = 1; i <= log; i++) 
            memo[u][i] = memo[memo[u][i - 1]][i - 1]; 
        for (int v : g[u]) { 
            if (v != p) { 
  
                // Calculating the level of each node 
                lev[v] = lev[u] + 1; 
                dfs(v, u); 
            } 
        } 
    } 
  
    // Function to return the LCA of nodes u and v 
    static int lca(int u, int v) 
    { 
        // The node which is present farthest 
        // from the root node is taken as u 
        // If v is farther from root node 
        // then swap the two 
        if (lev[u] < lev[v]) { 
            int temp = u; 
            u = v; 
            v = temp; 
        } 
  
        // Finding the ancestor of u 
        // which is at same level as v 
        for (int i = log; i >= 0; i--) { 
            if ((lev[u] - (int)Math.pow(2, i)) >= lev[v]) 
                u = memo[u][i]; 
        } 
  
        // If v is the ancestor of u 
        // then v is the LCA of u and v 
        if (u == v) 
            return u; 
  
        // Finding the node closest to the root which is 
        // not the common ancestor of u and v i.e. a node 
        // x such that x is not the common ancestor of u 
        // and v but memo[x][0] is 
        for (int i = log; i >= 0; i--) { 
            if (memo[u][i] != memo[v][i]) { 
                u = memo[u][i]; 
                v = memo[v][i]; 
            } 
        } 
  
        // Returning the first ancestor 
        // of above found node 
        return memo[u][0]; 
    } 
  
    // Driver code 
    public static void main(String args[]) 
    { 
  
        // Number of nodes 
        int n = 9; 
        g = new ArrayList[n + 1]; 
  
        // log(n) with base 2 
        log = (int)Math.ceil(Math.log(n) / Math.log(2)); 
        memo = new int[n + 1][log + 1]; 
  
        // Stores the level of each node 
        lev = new int[n + 1]; 
  
        // Initialising memo values with -1 
        for (int i = 0; i <= n; i++) 
            Arrays.fill(memo[i], -1); 
        for (int i = 0; i <= n; i++) 
            g[i] = new ArrayList<>(); 
  
        // Add edges 
        g[1].add(2); 
        g[2].add(1); 
        g[1].add(3); 
        g[3].add(1); 
        g[1].add(4); 
        g[4].add(1); 
        g[2].add(5); 
        g[5].add(2); 
        g[3].add(6); 
        g[6].add(3); 
        g[3].add(7); 
        g[7].add(3); 
        g[3].add(8); 
        g[8].add(3); 
        g[4].add(9); 
        g[9].add(4); 
        dfs(1, 1); 
        System.out.println("The LCA of 6 and 9 is " + lca(6, 9)); 
        System.out.println("The LCA of 5 and 9 is " + lca(5, 9)); 
        System.out.println("The LCA of 6 and 8 is " + lca(6, 8)); 
        System.out.println("The LCA of 6 and 1 is " + lca(6, 1)); 
    } 
} 

Python3

# Python3 implementation of the above approach 
import math
  
# Pre-processing to calculate values of memo[][]
def dfs(u, p, memo, lev, log, g):
      
    # Using recursion formula to calculate 
    # the values of memo[][] 
    memo[u][0] = p
    for i in range(1, log + 1):
        memo[u][i] = memo[memo[u][i - 1]][i - 1]
          
    for v in g[u]:
        if v != p:
            lev[v] = lev[u] + 1
            dfs(v, u, memo, lev, log, g)
  
# Function to return the LCA of nodes u and v 
def lca(u, v, log, lev, memo):
      
    # The node which is present farthest 
    # from the root node is taken as u 
    # If v is farther from root node 
    # then swap the two 
    if lev[u] < lev[v]:
        swap(u, v)
          
    # Finding the ancestor of u 
    # which is at same level as v 
    for i in range(log, -1, -1):
        if (lev[u] - pow(2, i)) >= lev[v]:
            u = memo[u][i]
              
    # If v is the ancestor of u 
    # then v is the LCA of u and v         
    if u == v:
        return v
          
    # Finding the node closest to the 
    # root which is not the common ancestor
    # of u and v i.e. a node x such that x
    # is not the common ancestor of u 
    # and v but memo[x][0] is 
    for i in range(log, -1, -1):
        if memo[u][i] != memo[v][i]:
            u = memo[u][i]
            v = memo[v][i]
      
    # Returning the first ancestor 
    # of above found node         
    return memo[u][0]
  
# Driver code 
  
# Number of nodes 
n = 9
  
log = math.ceil(math.log(n, 2))
g = [[] for i in range(n + 1)]
  
memo = [[-1 for i in range(log + 1)] 
            for j in range(n + 1)]
  
# Stores the level of each node             
lev = [0 for i in range(n + 1)]
  
# Add edges 
g[1].append(2)
g[2].append(1)
g[1].append(3)
g[3].append(1)
g[1].append(4)
g[4].append(1)
g[2].append(5)
g[5].append(2)
g[3].append(6)
g[6].append(3)
g[3].append(7)
g[7].append(3)
g[3].append(8)
g[8].append(3)
g[4].append(9)
g[9].append(4)
  
dfs(1, 1, memo, lev, log, g)
  
print("The LCA of 6 and 9 is", lca(6, 9, log, lev, memo))
print("The LCA of 5 and 9 is", lca(5, 9, log, lev, memo))
print("The LCA of 6 and 8 is", lca(
Структуры данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Различия между структурой данных массива и словаря
21 Января, 2023
TCS SDE Sheet: Вопросы и ответы для интервью
12 Января, 2023
Множественные сравнения в очереди приоритетов С++?
6 Января, 2023
Когда использовать Queue over ArrayList в Java?
6 Января, 2023
Введение в связанный список — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Введение в массивы — учебные пособия по структуре данных и алгоритмам
12 Декабря, 2022
Как подготовиться к ICFP или Международной конференции по функциональному программированию?
12 Декабря, 2022