Координатная геометрия
Координатная геометрия или аналитическая геометрия - это ветвь геометрии, в которой алгебраические уравнения используются для обозначения точек, линий и кривых. Координатная геометрия - это объединение алгебры и геометрии, в котором алгебра используется для изучения геометрических отношений, а геометрические фигуры представляются с помощью уравнений. Самая популярная система координат - прямоугольная декартова система. Координаты точки - это реальные переменные, связанные для описания ее положения в пространстве. Здесь мы считаем пространство двумерным. Давайте посмотрим на следующие термины.
- Начало: через точку O, называемую началом координат, мы берем две взаимно перпендикулярные линии XOX 'и YOY' и называем их осями x и y соответственно.
- Абсцисса и ордината: положение точки полностью определяется относительно этих осей с помощью упорядоченной пары действительных чисел (x, y), называемых координатами P, где | х | и | y | являются расстояниями точки P от оси y и оси x соответственно, x называется координатой x или абсциссой P, а y называется координатой y или ординатой точки P.
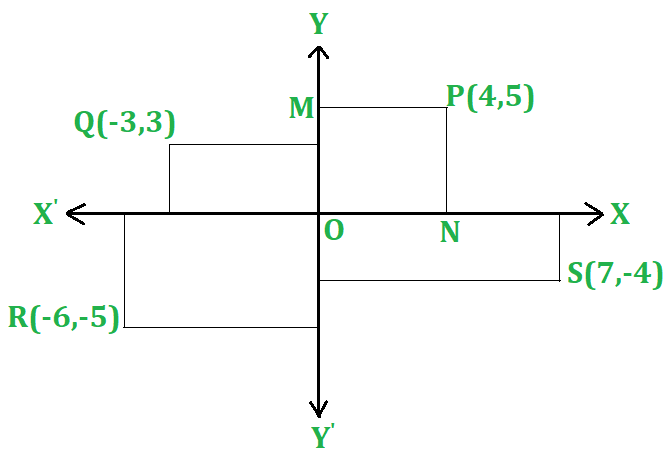
Пусть P - точка на плоскости; нарисуйте две перпендикулярные линии X'OX, Y'OY на плоскости и проведите PM, PN параллельно OX, OY соответственно. X'OX, Y'OY известны как оси координат. MP - координата x, называемая абсциссой , а NP - координата y, называемая ординатой P.
Полярные координаты
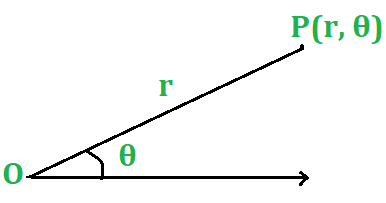
Пусть OX - заданная прямая, а P - любая точка в заданной плоскости. Пусть 0 - угол, на который поворачивается линия при движении из OX в позицию OP. Тогда, если r - длина OP, положение P известно, когда известны r и θ. r называется радиус-вектором, векторным углом, а (r, θ) - полярными координатами точки P, которая кратко обозначается точкой (r, θ). OX называется начальной линией, а O - полюсом.
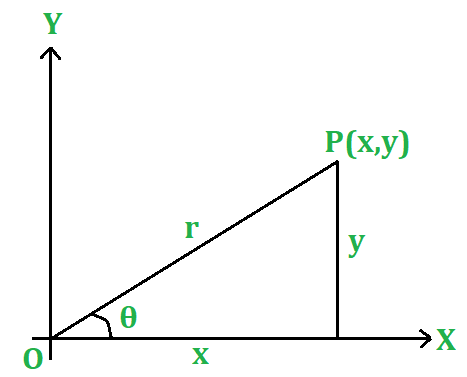
Связь между декартовыми и полярными координатами
Пусть P будет точкой (x, y) относительно прямоугольных осей OX, OY и точкой (r, θ) относительно полюса O и начальной прямой OX. то есть ось X. Имеем x = rcosθ; y = rsinθ Следовательно, tanθ = y / x и x 2 + y 2 = r 2 Х Эти соотношения позволяют нам переходить от одной системы координат к другой.
Расстояние между двумя точками
Расстояние между двумя точками A (x1, y1) и B (x2, y2) определяется выражением
AB = √((x2 – x1)2 + (y2 – y1)2)
Расстояние точки P (x, y) от начала координат O (0, 0) задается
OP = √((x – 0)2+ (y – 0)2), i.e. OP = √(x² + y²)
Примеры
Пример 1. Найти расстояние между точками P (-4, 7) и Q (2, -5)?
Решение:
The given points are P(-4, 7) and Q(2, -5).
Then, (x1 = -4, y1 = 7) and (x2 = 2, y2 = -5). :
PQ = √((x2 – x1)2 + (y2 – y1)2)
= √((2 – (-4))2 + (-5 – 7)2)
= √(62 + (-12)2)
= √(36 + 144)
= √180
= 6√5
Пример 2: Найти расстояние от точки P (6, -6) до начала координат?
Решение:
Let P(6, -6) be the given point and O(0, 0) be the origin.
Then, OP = √((6 – 0)2 + (-6 – 0)2)
= √(62 + (-6)2)
= √72
= 6√2
Формула сечения
Координаты точки P (x, y), которая разделяет отрезок прямой, соединяющий A (x1, y1) и B (x2, y2) внутри в соотношении m: n, задаются следующим образом:
x = (mx2 + nx1) / (m+n)
y = (my2+ny1) / (m+n)
Примеры
Пример 1. Найти координаты средней точки отрезка, соединяющего точки A (-5, 4) и B (7, -8)?
Решение:
Let M(x, y) be the midpoint of AB. Then,
x = ((-5) + 7)/2 =1 and y = ((4 + (-8)) = -2
Hence, the required point is M (1, -2).
Пример 2: Найти координаты точек трисечения отрезка прямой, соединяющего точки A (-5, 6) и B (4, -3)?
Решение:
Let P and Q be the points of trisection of AB.
Then, P divides AB in the ratio 1 : 2
So, the coordinates of P are
P((1 x 4 + 2 x (-5)/1 + 2, ((1 x (-3) + 2 x 6)/1 + 2) i.e., P(-2, 3).
Also, Q divides AB in the ratio 2:1.
So, the coordinates of Q are
Q((2 x 4 + 1 x (-5)/2 + 1, (2x(-3) +1 x 6/1 + 2)) i.e., Q(1, 0)
Q(1, 0).
Площадь Трингл
Площадь треугольника ABC с вершинами A (x1, y1), B (x2, y2) и C (x3, y3) равна
area(ABC) = |1/2 {x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)}|
Примеры
Пример 1. Найдите площадь треугольника, вершины которого - A (2, 7), B (3, -1) и C (-5, 6)?
Решение:
Let A(2, 7), B(3, -1) and C(-5, 6) be the vertices of the given △ABC.
Then,
(x1 = 2, y1 = 7), (x2 = 3, y2 = -1) and (x3 = -5, y3 = 6).
Area of △ABC = 1/2|{x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)}|
= 1/2 |2(-1 – 6) + 3(6 – 7) – 5(7 +1)|
= 1/2| -14 – 3 – 40|
= 1/2|-57|
= 57/2
= 28.5 sq units.
Пример 2: Найдите площадь четырехугольника ABCD, вершины которого - A (-4, -2), B (-3, -5), C (3, -2) и D (2, 3).
Решение:
Join A and C. Then, area of quad. ABCD = ar(△ABC) + ar(△ACD)
Area of △ABC = 1/2|{(-4).(-5 + 2) -3(-2 + 2) + 3(-2 + 5)}|
= 21/2 sq units.
Area of △ACD = 1/2|{ (-4).(-2 – 3) + 3(3 + 2) + 2(-2 + 2}|
= 35/2
Area of quad. ABCD = 21/2 + 35/2 sq units = 28 sq units.
Условие коллинеарности трех точек.
Пусть даны точки A (x1, y1), B (x2, y2) и C (x3, y3). Тогда A, B и C коллинеарны,
⇒ area of ABC = 0
⇒ 1/2.[x1(y2 – y1) + x2(y3 – y1) + x3(y1 – y2)] = 0
Примеры
Пример 1. Покажите, что точки A (-1, 1), B (5, 7) и C (8,10) лежат на одной прямой.
Решение:
Let A(-1, 1), B(5, 7) and C(8, 10) be the given points.
Then, (x1 = -1, y = 1), (x2 = 5, y2 = 7) and (x3 = 8, y3 = 10)
∴ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
= (-1) (7 – 10) + 5(10 -1) + 8(1 – 7)
= (3 + 45 – 48)
= 0
Hence, the given points are collinear.
Пример 2: Покажите, что точки A (a, b + c), B (b, c + a) и C (c, a + b) лежат на одной прямой.
Решение:
Let A(a, b + c), B(b, c + a) and C(c, a + b) be the given points.
Then, (x1 = a, y1 = b + c); (x2 = b, y2 = c + a); and (x3 = c, y3 = a + b).
∴ a(c + a – a – b) + b(a + b – b – c) + c(b + c – c – a)
= a(c – b) + b(a – c)+ c(b – a)
= 0
Hence, the given points are collinear.