Конгруэнтность треугольников

Теорема Пифагора - это своего рода столп геометрии. В математике теорема Пифагора или теорема Пифагора - это фундаментальное соотношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника. Давайте посмотрим на фактическую концепцию и примеры теоремы Пифагора.

Утверждение теоремы Пифагора

Если у нас есть треугольник, и треугольник должен быть прямоугольным, то есть один из трех углов в треугольнике должен составлять 90 градусов. Теперь, с помощью теоремы Пифагора, если мы знаем две стороны прямоугольного треугольника, мы можем найти третью сторону.

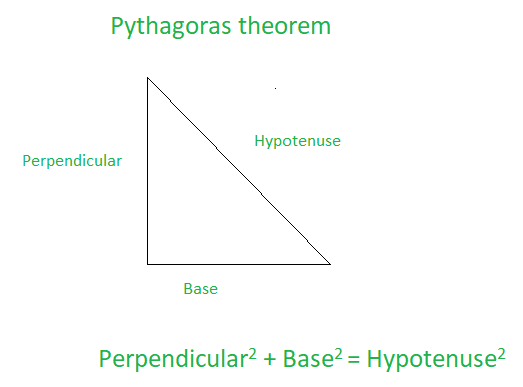
Самая длинная сторона прямоугольного треугольника - это сторона, противоположная прямому углу, который является гипотенузой. Кроме того, на приведенной выше диаграмме мы можем видеть, что квадрат из двух сторон, примыкающий к углу в 90 градусов, равен квадрату гипотенузы.

Примеры теорем Пифагора

Давайте посмотрим на несколько основных примеров теоремы Пифагора.

Пример 1: Определить высоту равностороннего треугольника со стороной 16?

Решение:

For the given problem we can split the triangle into two equal parts from which we can get the hypotenuse length is 16 units. And the other leg is 8 units i.e. half of 16 units. So, let the height be x.

According to question,

x² + 8² = 16²

=> x² = 192

=> x = √192

Taking positive value of x

=> x = 13.86 units

Hence, the required height is 13.86 units.

Пример 2: Мужчина идет на 60 м на запад, затем на 60 м на север. Найти его расстояние от отправной точки?

Решение:

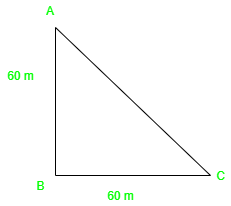
According to the given question, we can draw the diagram as shown above and we have to find the distance AC.

Now, According to the Pythagoras theorem, we can get the equation as

                                 AB² + BC ² = AC²

                                   =>  AC² = 60²  + 60 ²

                          =>  AC²  = 7200

                          =>  AC  =  √7200

                          =>  AC =  84.85 m ( Since, it is a distance unit. Therefore taking positive value of square root)

Hence, the required distance is 84.85 m.

Постулаты / критерии конгруэнтности треугольника

а. SSS (Сторона, Сторона, Сторона)

Согласно постулату SSS, если все три стороны треугольника равны соответствующим трем сторонам другого треугольника, то он удовлетворяет условию SSS.

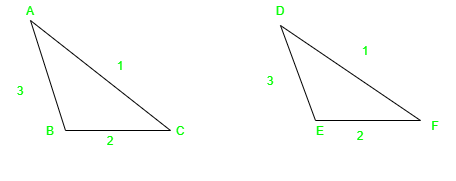
На приведенном выше рисунке видно, что AB = DE, AC = DF и BC = EF. Следовательно, Δ ABC ≅ ΔDEF

б. SAS (Боковой, Угловой, Боковой)

В постулате САС, сравнение двух треугольников, если две стороны и угол между двумя сторонами равны. Тогда он удовлетворяет условию SAS.

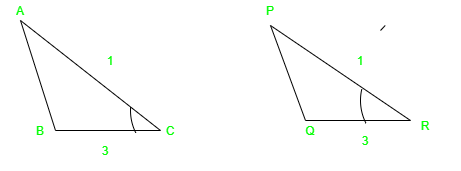
На приведенном выше рисунке мы видим, что AC = PR, BC = QR и ∠C = ∠R. Следовательно, ΔACB ≅ ΔPRQ.

v. ASA (угол, сторона, угол)

Здесь, если у нас есть два треугольника, где любые два угла и стороны, включенные между двумя углами одного треугольника, равны углам и стороне соответствующего треугольника. Тогда два треугольника будут удовлетворять конгруэнтности ASA.

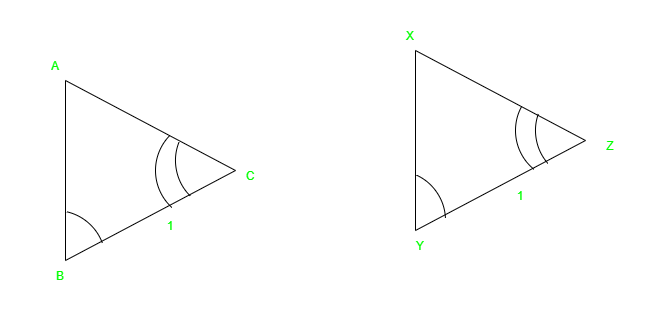
На приведенном выше рисунке видно, что BC = YZ, ∠B = ∠Y и ∠C = ∠Z. Следовательно, ΔACB ≅ ΔXZY.

d. AAS (угол, угол, сторона)

Если любые два угла треугольника и не включенная сторона равны двум углам и стороне соответствующего треугольника. Тогда он будет удовлетворять конгруэнтности AAS.

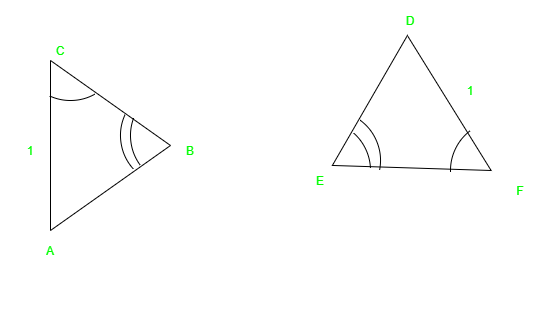
Из приведенного рисунка можно сказать, что,

AC = DF,

∠B = ∠E,

и ∠C = ∠F

Следовательно, ΔACB ≅ ΔDFE

е. RHS (Прямой угол - Гипотенуза - Сторона)

Критерии RHS удовлетворяются только прямоугольным треугольником. Итак, в конгруэнтности RHS, если только две стороны, т.е. гипотенуза и одна сторона прямоугольного треугольника, равны соответствующей гипотенузе и стороне другого прямоугольного треугольника. Тогда можно сказать, что RHS доволен.

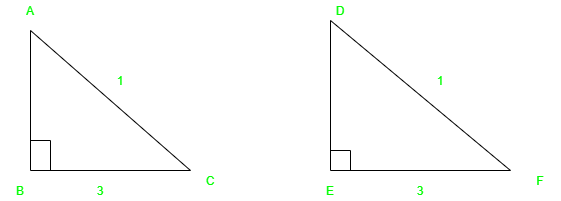
Из приведенного выше примера прямоугольного треугольника получаем AC = DF и BC = EF. Следовательно, ΔACB ≅ ΔDFE.

Почему SSA не является постулатом / критерием конгруэнтности?

Доказательство:

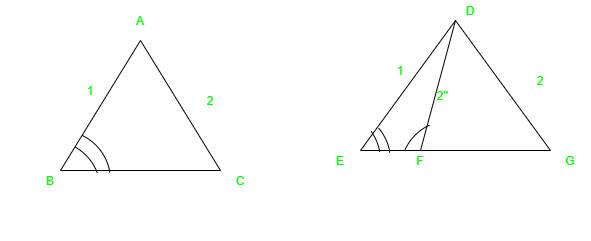
Let’s first see in Δ ABC and Δ DEG

∠B = ∠E, AB= DE and AC = DG    

So, from this above condition, we cannot justify that Δ ABC ≅  ΔDEG. To understand this, let’s construct a line DF in Δ DEG as shown above, and DF is congruent to AC and DG. We have got a new triangle i.e. Δ DEF.

Now, we can see that AC is congruent to DF, ∠B = ∠E, and AC = DE. But,  Δ ABC is not congruent to ΔDEF. Because of which we can make a conclusion that SSA is not only sufficient to tell that triangles are congruent. Therefore, it is important to know the ∠A and ∠D means the angle between the two sides.

There is only one exceptional case which we have seen in the RHS postulate, on which SSA or ASS postulate will get satisfied. Henceforth, in a general or common scenario, SSA or ASS postulate will not be satisfying.